One atom basis phonons in 2D

[Click here for a PDF of this post with nicer formatting]

Let’s tackle a problem like the 2D problem of the final exam, but first more generally. Instead of a square lattice consider the lattice with the geometry illustrated in fig. 1.1.

Fig 1.1: Oblique one atom basis

Here, and are the vector differences between the equilibrium positions separating the masses along the and interaction directions respectively. The equilibrium spacing for the cross coupling harmonic forces are

Based on previous calculations, we can write the equations of motion by inspection

Inserting the trial solution

and using the matrix form for the projection operators, we have

This fully specifies our eigenvalue problem. Writing

we wish to solve

Neglecting the specifics of the matrix at hand, consider a generic two by two matrix

for which the characteristic equation is

So our angular frequencies are given by

The square root can be simplified slightly

so that, finally, the dispersion relation is

Our eigenvectors will be given by

or

So, our eigenvectors, the vectoral components of our atomic displacements, are

or

Square lattice

There is not too much to gain by expanding out the projection operators explicitly in general. However, let’s do this for the specific case of a square lattice (as on the exam problem). In that case, our projection operators are

Our matrix is

where, specifically, the squared sines for this geometry are

Using eq. 1.0.6, the dispersion relation and eigenvectors are

This calculation is confirmed in oneAtomBasisPhononSquareLatticeEigensystem.nb. Mathematica calculates an alternate form (equivalent to using a zero dot product for the second row), of

Either way, we see that leads to only horizontal or vertical motion.

With the exam criteria

In the specific case that we had on the exam where and , these are

For horizontal and vertical motion we need , or for a difference in the absolute values of the sine arguments

That is, one of

In the first BZ, that is one of or .

System in rotated coordinates

On the exam, where we were asked to solve for motion along the cross directions explicitly, there was a strong hint to consider a rotated (by ) coordinate system.

The rotated the lattice basis vectors are , and the projection matrices. Writing and , where , or . In the basis the projection matrices are

The dot products that show up in the squared sines are

So that in this basis

With the rotated projection operators eq. 1.0.5.5 takes the form

This clearly differs from eq. 1.0.16d, and results in a different expression for the eigenvectors, but the same as eq. 1.0.20.20 for the angular frequencies.

or, equivalently

For the and case of the exam, this is

Similar to the horizontal coordinate system, we see that we have motion along the diagonals when

or one of

Stability?

The exam asked why the cross coupling is required for stability. Clearly we have more complex interaction. The constant surfaces will also be more complex. However, I still don’t have a good intuition what exactly was sought after for that part of the question.

Numerical computations

A Manipulate allowing for choice of the spring constants and lattice orientation, as shown in fig. 1.2, is available in phy487/oneAtomBasisPhonon.nb. This interface also provides a numerical calculation of the distribution relation as shown in fig. 1.3, and provides an animation of the normal modes for any given selection of and (not shown).

Fig 1.2: 2D Single atom basis Manipulate interface

Fig 1.3: Sample distribution relation for 2D single atom basis.

Two body harmonic oscillator in 3D, and 2D diamond lattice vibrations

Abridged harmonic oscillator notes

[This is an abbreviation of more extensive PDF notes associated with the latter part of this post.]

Motivation and summary of harmonic oscillator background

After having had some trouble on a non-1D harmonic oscillator lattice problem on the exam, I attempted such a problem with enough time available to consider it properly. I found it helpful to consider first just two masses interacting harmonically in 3D, each displaced from an equilibrium position.

The Lagrangian that described this most naturally was found to be

This was solved in absolute and displacement coordinates, and then I moved on to consider a linear expansion of the harmonic potential about the equilibrium point, a problem closer to the exam problem (albeit still considering only two masses). The equilibrium points were described with vectors as in fig. 2.1, where .

fig 2.1: Direction cosines relative to equilibrium position difference vector

 

Using such coordinates, and generalizing, it was found that the complete Lagrangian, to second order about the equilibrium positions, is

Evaluating the Euler-Lagrange equations, the equations of motion for the displacements were found to be

or

Observe that on the RHS above we have a projection operator, so we could also write

We see that the equations of motion for the displacements of a system of harmonic oscillators has a rather pleasant expression in terms of projection operators, where we have projections onto the unit vectors between each pair of equilibrium position.

A number of harmonically coupled masses

Now let’s consider masses at lattice points indexed by a lattice vector , as illustrated in fig. 2.2.

fig 2.2: Masses harmonically coupled in a lattice

 

With a coupling constant of between lattice points indexed and (located at and respectively), and direction cosines for the equilibrium direction vector between those points given by

the Lagrangian is

Evaluating the Euler-Lagrange equations for the mass at index we have

and

where . Equating both, we have in vector form

or

This is an intuitively pleasing result. We have displacement and the direction of the lattice separations in the mix, but not the magnitude of the lattice separation itself.

Two atom basis, 2D diamond lattice

As a concrete application of the previously calculated equilibrium harmonic oscillator result, let’s consider a two atom basis diamond lattice where the horizontal length is and vertical height is .

Indexing for the primitive unit cells is illustrated in fig. 2.3.

fig 2.3: Primitive unit cells for rectangular lattice

 

Let’s write

For mass assume a trial solution of the form

The equations of motion for the two particles are

Insertion of the trial solution gives

Regrouping, and using the matrix form for the projection operators, this is

As a single matrix equation, this is

Observe that this is an eigenvalue problem for matrix

and eigenvalues .

To be explicit lets put the and functions in explicit matrix form. The orthogonal projectors have a simple form

For the and projection operators, we can use half angle formulations

After some manipulation, and the following helper functions

the block matrices of eq. 2.0.17.17 take the form

A final bit of simplification for possible, noting that , and , so

and

It isn’t particularly illuminating to expand out the determinant for such a system, even though it can be done symbolically without too much programming. However, what is easy after formulating the matrix for this system, is actually solving it. This is done, and animated, in twoAtomBasisRectangularLatticeDispersionRelation.cdf

Exponential solutions to second order linear system

[Click here for a PDF of this post with nicer formatting (especially if my latex to wordpress script has left FORMULA DOES NOT PARSE errors.)]

Motivation

We’re discussing specific forms to systems of coupled linear differential equations, such as a loop of “spring” connected masses (i.e. atoms interacting with harmonic oscillator potentials) as sketched in fig. 1.1.

Fig 1.1: Three springs loop

 

Instead of assuming a solution, let’s see how far we can get attacking this problem systematically.

Matrix methods

Suppose that we have a set of 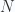masses constrained to a circle interacting with harmonic potentials. The Lagrangian for such a system (using modulo 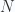indexing) is

The force equations follow directly from the Euler-Lagrange equations

For the simple three particle system depicted above, this is

with equations of motion

Let’s partially non-dimensionalize this. First introduce average mass and spring constants , and rearrange slightly

With

Our system takes the form

We can at least theoretically solve this in a simple fashion if we first convert it to a first order system. We can do that by augmenting our vector of displacements with their first derivatives

So that

Now the solution is conceptually trivial

We are however, faced with the task of exponentiating the matrix . All the powers of this matrix will be required, but they turn out to be easy to calculate

allowing us to write out the matrix exponential

Case I: No zero eigenvalues

Provided that 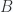has no zero eigenvalues, we could factor this as

This initially leads us to believe the following, but we’ll find out that the three springs interaction matrix 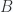does have a zero eigenvalue, and we’ll have to be more careful. If there were any such interaction matrices that did not have such a zero we could simply write

This is

The solution, written out is

so that

As a check differentiation twice shows that this is in fact the general solution, since we have

and

Observe that this solution is a general solution to second order constant coefficient linear systems of the form we have in eq. 1.5. However, to make it meaningful we do have the additional computational task of performing an eigensystem decomposition of the matrix 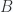. We expect negative eigenvalues that will give us oscillatory solutions (ie: the matrix square roots will have imaginary eigenvalues).

Example: An example diagonalization to try things out

{example:threeSpringLoop:1}{

Let’s do that diagonalization for the simplest of the three springs system as an example, with and , so that we have

A orthonormal eigensystem for 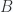is

With

We have

We also find that 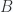and its root are intimately related in a surprising way

We also see, unfortunately that 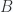has a zero eigenvalue, so we can’t compute . We’ll have to back and up and start again differently.
}

Case II: allowing for zero eigenvalues

Now that we realize we have to deal with zero eigenvalues, a different approach suggests itself. Instead of reducing our system using a Hamiltonian transformation to a first order system, let’s utilize that diagonalization directly. Our system is

where and

Let

so that our system is just

or

This is 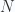equations, each decoupled and solvable by inspection. Suppose we group the eigenvalues into sets . Our solution is then

Transforming back to lattice coordinates using , we have

We see that the zero eigenvalues integration terms have no contribution to the lattice coordinates, since , for all .

If are a set of not necessarily orthonormal eigenvectors for 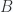, then the vectors , where are the reciprocal frame vectors. These can be extracted from (i.e., the rows of ). Taking dot products between with and , provides us with the unknown coefficients

Supposing that we constrain ourself to looking at just the oscillatory solutions (i.e. the lattice does not shake itself to pieces), then we have

Eigenvectors for eigenvalues that were degenerate have been explicitly enumerated here, something previously implied. Observe that the dot products of the form have been put into projector operator form to group terms more nicely. The solution can be thought of as a weighted projector operator working as a time evolution operator from the initial state.

Example: Our example interaction revisited

{example:threeSpringLoop:2}{

Recall that we had an orthonormal basis for the eigensubspace for the interaction example of eq. 1.20 again, so . We can sum to find

The leading matrix is an orthonormal projector of the initial conditions onto the eigen subspace for . Observe that this is proportional to 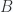itself, scaled by the square of the non-zero eigenvalue of . From this we can confirm by inspection that this is a solution to , as desired.
}

Fourier transform methods

Let’s now try another item from our usual toolbox on these sorts of second order systems, the Fourier transform. For a one variable function of time let’s write the transform pair as

One mass harmonic oscillator

The simplest second order system is that of the harmonic oscillator

Application of the transform gives

We clearly have a constraint that is a function of frequency, but one that has to hold for all time. Let’s transform this constraint to the frequency domain to consider that constraint independent of time.

How do we make sense of this?

Since 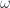is an integration variable, we can’t just mandate that it equals the constant driving frequency . It’s clear that we require a constraint on the transform as well. As a trial solution, imagine that

latex \left\lvert {\omega – \pm \omega_\circ} \right\rvert < \omega_{\text{cutoff}}$} \\ 0 & \quad \mbox{otherwise}\end{array}\right.\end{aligned} \hspace{\stretch{1}}(1.0.35.35)$

This gives us

Now it is clear that we can satisfy our constraint only if the interval is made infinitesimal. Specifically, we require both a constraint and that the transform have a delta function nature. That is

Substitution back into our transform gives

We can verify quickly that this satisfies our harmonic equation .

Two mass harmonic oscillator

Having applied the transform technique to the very simplest second order system, we can now consider the next more complex system, that of two harmonically interacting masses (i.e. two masses on a frictionless spring).

F1

Our system is described by

and the pair of Euler-Lagrange equations

The equations of motion are

Let

Insertion of these transform pairs into our equations of motion produces a pair of simultaneous integral equations to solve

As with the single spring case, we can decouple these equations with an inverse transformation operation , which gives us (after dropping primes)

Taking determinants gives us the constraint on the frequency

Introducing a reduced mass

the pair of solutions are

As with the single mass oscillator, we require the functions to also be expressed as delta functions. The frequency constraint and that delta function requirement together can be expressed, for as

With a transformation back to time domain, we have functions of the form

Back insertion of these into the equations of motion, we have

Equality requires identity for all powers of , or

or and

Observe that

(with a similar alternate result). We can rewrite eq. 1.0.35.35 as

It’s clear that there’s two pairs of linear dependencies here, so the determinant is zero as expected. We can read off the remaining relations. Our undetermined coefficients are given by

Observe that the constant term is not really of interest, since it represents a constant displacement of both atoms (just a change of coordinates).

Check:

Reflection

We’ve seen that we can solve any of these constant coefficient systems exactly using matrix methods, however, these will not be practical for large systems unless we have methods to solve for all the non-zero eigenvalues and their corresponding eigenvectors. With the Fourier transform methods we find that our solutions in the frequency domain is of the form

or in the time domain

We assumed exactly this form of solution in class. The trial solution that we used in class factored out a phase shift from of the form of , but that doesn’t change the underling form of that assumed solution. We have however found a good justification for the trial solution we utilized.

A final pre-exam update of my notes compilation for ‘PHY452H1S Basic Statistical Mechanics’, Taught by Prof. Arun Paramekanti

Here’s my third update of my notes compilation for this course, including all of the following:

April 21, 2013 Fermi function expansion for thermodynamic quantities

April 20, 2013 Relativistic Fermi Gas

April 10, 2013 Non integral binomial coefficient

April 10, 2013 energy distribution around mean energy

April 09, 2013 Velocity volume element to momentum volume element

April 04, 2013 Phonon modes

April 03, 2013 BEC and phonons

April 03, 2013 Max entropy, fugacity, and Fermi gas

April 02, 2013 Bosons

April 02, 2013 Relativisitic density of states

March 28, 2013 Bosons

plus everything detailed in the description of my previous update and before.

PHY452H1S Basic Statistical Mechanics. Lecture 21: Phonon modes. Taught by Prof. Arun Paramekanti

[Click here for a PDF of this post with nicer formatting (especially if my latex to wordpress script has left FORMULA DOES NOT PARSE errors.)]

Disclaimer

Peeter’s lecture notes from class. May not be entirely coherent.

These are notes for the last class, which included a lot of discussion not captured by this short set of notes (as well as slides which were not transcribed).

Phonon modes

If we model a solid as a set of interconnected springs, as in fig. 1.1, then the potentials are of the form

Fig 1.1: Solid oscillator model

 

with kinetic energies

It’s possible to introduce generalized forces

Can differentiate

Assuming a Fourier representation

we find

This looks like a harmonic oscillator with

This is plotted in fig. 1.2. In particular note that for for we can use a linear approximation

Fig 1.2: Angular frequency of solid oscillator model

 

Experimentally, looking at specific for a complex atomic structure like Gold, we find for example good fit for a model such as

An updated compilation of notes, for ‘PHY452H1S Basic Statistical Mechanics’, Taught by Prof. Arun Paramekanti

In A compilation of notes, so far, for ‘PHY452H1S Basic Statistical Mechanics’ I posted a link this compilation of statistical mechanics course notes.

That compilation now all of the following too (no further updates will be made to any of these) :

February 28, 2013 Rotation of diatomic molecules

February 28, 2013 Helmholtz free energy

February 26, 2013 Statistical and thermodynamic connection

February 24, 2013 Ideal gas

February 16, 2013 One dimensional well problem from Pathria chapter II

February 15, 2013 1D pendulum problem in phase space

February 14, 2013 Continuing review of thermodynamics

February 13, 2013 Lightning review of thermodynamics

February 11, 2013 Cartesian to spherical change of variables in 3d phase space

February 10, 2013 n SHO particle phase space volume

February 10, 2013 Change of variables in 2d phase space

February 10, 2013 Some problems from Kittel chapter 3

February 07, 2013 Midterm review, thermodynamics

February 06, 2013 Limit of unfair coin distribution, the hard way

February 05, 2013 Ideal gas and SHO phase space volume calculations

February 03, 2013 One dimensional random walk

February 02, 2013 1D SHO phase space

February 02, 2013 Application of the central limit theorem to a product of random vars

January 31, 2013 Liouville’s theorem questions on density and current

January 30, 2013 State counting

Some problems from Kittel chapter 3

[Click here for a PDF of this post with nicer formatting (especially if my latex to wordpress script has left FORMULA DOES NOT PARSE errors.)]

Question: Classical gas partition function

[1] expresses the classical gas partition function (3.77) as

Show that this leads to the expected result for the thermal average energy.

Answer

Let’s use the adjustment technique from the text for the partition case and write

with as above. This gives us

Question: Two state system

[1] problem 3.1.

Find an expression for the free energy as a function of of a system with two states, one at energy and one at energy . From the free energy, find expressions for the energy and entropy of the system.

Answer

Our partition function is

The free energy is just

The entropy follows immediately

The energy is

This is

These are all plotted in (Fig 1).

Fig1: Plots for two state system

 

\imageFigure{kittelCh3Problem1PlotsFig1}{Plots for two state system}{fig:kittelCh3Problem1Plots:kittelCh3Problem1PlotsFig1}{0.2}

Question: Magnetic susceptibility

[1] problem 3.2.

Use the partition function to find an exact expression for the magnetization and the susceptibility as a function of temperature and magnetic field for the model system of magnetic moments in a magnetic field. The result for the magnetization, found by other means, was , where is the particle concentration. Find the free energy and express the result as a function only of and the parameter . Show that the susceptibility is in the limit .

Answer

Our partition function for a unit volume containing spins is

so that the Free energy is

The energy, magnetization and magnetic field were interrelated by

This gives us

so that

For , the cosh term goes to unity, so we have

as desired.

With , or , the free energy is

That last expression isn’t particularly illuminating. What was the point of that substitution?

Question: Free energy of a harmonic oscillator

[1] problem 3.3.

A one dimensional harmonic oscillator has an infinite series of equally spaced energy states, with , where is a positive integer or zero, and is the classical frequency of the oscillator. We have chosen the zero of energy at the state . Show that for a harmonic oscillator the free energy is

Note that at high temperatures such that we may expand the argument of the logarithm to obtain . From 1.0.16 show that the entropy is

Answer

I found it curious that this problem dropped the factor of from the energy. Including it we have

So that the partition function is

The free energy is

We see that the contribution of the in the energy of each state just adds a constant factor to the free energy. This will drop out when we compute the entropy. Dropping that factor now that we know why it doesn’t contribute, we can complete the summation, so have, by inspection

Taking derivatives for the entropy we have

Question: Energy fluctuation

[1] problem 3.4.

Consider a system of fixed volume in thermal contact with a reservoir. Show that the mean square fluctuation in the energy of the system is

Here is the conventional symbol for . Hint: Use the partition function to relate to the mean square fluctuation. Also, multiply out the term .

Answer

With a probability of finding the system in state of

the average energy is

So we have

But

giving

which shows 1.0.23 as desired.

References

[1] C. Kittel and H. Kroemer. Thermal physics. WH Freeman, 1980.

PHY456H1F: Quantum Mechanics II. Lecture 8 (Taught by Prof J.E. Sipe). Time dependent pertubation (cont.)

[Click here for a PDF of this post with nicer formatting (especially if my latex to wordpress script has left FORMULA DOES NOT PARSE errors.)]

Disclaimer.

Peeter’s lecture notes from class. May not be entirely coherent.

Time dependent pertubation.

We’d gotten as far as calculating

where

and

Graphically, these frequencies are illustrated in figure (\ref{fig:qmTwoL8fig0FrequenciesAbsorbtionAndEmission})

\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{qmTwoL8fig0FrequenciesAbsorbtionAndEmission}
\caption{Positive and negative frequencies.}
\end{figure}

The probability for a transition from to is therefore

Recall that because the electric field is real we had

Suppose that we have a wave pulse, where our field magnitude is perhaps of the form

as illustated with in figure (\ref{fig:gaussianWavePacket}).

\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{gaussianWavePacket}
\caption{Gaussian wave packet}
\end{figure}

We expect this to have a two lobe Fourier spectrum, with the lobes centered at , and width proportional to .

For reference, as calculated using Mathematica this Fourier transform is

This is illustrated, again for , in figure (\ref{fig:FTgaussianWavePacket})

\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{FTgaussianWavePacket}
\caption{FTgaussianWavePacket}
\end{figure}

where we see the expected Gaussian result, since the Fourier transform of a Gaussian is a Gaussian.

FIXME: not sure what the point of this was?

Sudden pertubations.

Given our wave equation

and a sudden pertubation in the Hamiltonian, as illustrated in figure (\ref{fig:suddenStepHamiltonian})

\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{suddenStepHamiltonian}
\caption{Sudden step Hamiltonian.}
\end{figure}

Consider and fixed, and decrease . We can formally integrate 3.8

For

While this is an exact solution, it is also not terribly useful since we don’t know . However, we can select the small interval , and write

Note that we could use the integral kernel iteration technique here and substitute and then develop this, to generate a power series with dependence. However, we note that 3.11 is still an exact relation, and if , with the integration limits narrowing (provided is well behaved) we are left with just

Or

provided that we change the Hamiltonian fast enough. On the surface there appears to be no consequences, but there are some very serious ones!

Example: Harmonic oscillator.

Consider our harmonic oscillator Hamiltonian, with

Here continuously, but very quickly. In effect, we have tightened the spring constant. Note that there are cases in linear optics when you can actually do exactly that.

Imagine that is in the ground state of the harmonic oscillator as in figure (\ref{fig:suddenHamiltonianPertubationHO})

\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{suddenHamiltonianPertubationHO}
\caption{Harmonic oscillator sudden Hamiltonian pertubation.}
\end{figure}

and we suddenly change the Hamilontian with potential (weakening the “spring”). Professor Sipe gives us a graphical demo of this, by impersonating a constrained wavefunction with his arms, doing weak chicken-flapping of them. Now with the potential weakended, he wiggles and flaps his arms with more freedom and somewhat chaotically. His “wave function” arms are now bouncing around in the new limiting potential (initally over doing it and then bouncing back).

We had in this case the exact relation

but we also have

and

So

and at later times

whereas

So, while the wave functions may be exactly the same after such a sudden change in Hamiltonian, the dynamics of the situation change for all future times, since we now have a wavefunction that has a different set of components in the basis for the new Hamiltonian. In particular, the evolution of the wave function is now significantly more complex.

FIXME: plot an example of this.

Adiabatic pertubations.

FIXME: what does Adiabatic mean in this context. The usage in class sounds like it was just “really slow and gradual”, yet this has a definition “Of, relating to, or being a reversible thermodynamic process that occurs without gain or loss of heat and without a change in entropy”.

This is treated in section 17.5.2 of the text [1].

This is the reverse case, and we now vary the Hamiltonian very slowly.

We first consider only non-degenerate states, and at write

and

Imagine that at each time we can find the “instantaneous” energy eigenstates

These states do not satisfy Schr\”{o}dinger’s equation, but are simply solutions to the eigen problem. Our standard strategy in pertubation is based on analysis of

Here instead

we will expand, not using our initial basis, but instead using the instananeous kets. Plugging into Schr\”{o}dinger’s equation we have

This was complicated before with matrix elements all over the place. Now it is easy, however, the time derivative becomes harder. Doing that we find

We bra into this

and find

If the Hamiltonian is changed very very slowly in time, we can imagine that is also changing very very slowly, but we are not quite there yet. Let’s first split our sum of bra and ket products

into and terms. Looking at just the term

we note

Something plus its complex conjugate equals 0

so must be purely imaginary. We write

where is real.

References

[1] BR Desai. Quantum mechanics with basic field theory. Cambridge University Press, 2009.

Curious problem using the variational method to find the ground state energy of the Harmonic oscillator (cont.)

Picking up where this problem was last abandoned.

[Click here for a PDF of this post with nicer formatting (especially if my latex to wordpress script has left FORMULA DOES NOT PARSE errors.)]

Calculating the Fourier terms

Our wave function, with is plotted in figure (\ref{fig:expMinusBetsAbsX})

\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{expMinusBetsAbsX}
\caption{Exponential trial function with absolute exponential die off.}
\end{figure}

The zeroth order fitting using the gaussian exponential is found to be

With , this is plotted in figure (\ref{fig:expMinusBetsAbsXfirstOrderFitting}) and can be seen to match fairly well

\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{expMinusBetsAbsXfirstOrderFitting}
\caption{First ten orders, fitting harmonic oscillator wavefunctions to this trial function.}
\end{figure}

The higher order terms get small fast, but we can see in figure (\ref{fig:expMinusBetsAbsXtenthOrderFitting}), where a tenth order fitting is depicted that it would take a number of them to get anything close to the sharp peak that we have in our exponential trial function.

\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{expMinusBetsAbsXtenthOrderFitting}
\caption{Tenth order harmonic oscillator wavefunction fitting.}
\end{figure}

Note that the all the brakets of even orders in with the trial function are zero, which is why the tenth order approximation is only a sum of six terms.

Details for this \href{https://github.com/peeterjoot/physicsplay/blob/master/notes/phy456/gaussian\

The question of interest is why if we can approximate the trial function so nicely (except at the origin) even with just a first order approximation (polynomial times gaussian functions where the polynomials are Hankel functions), and we can get an exact value for the lowest energy state using the first order approximation of our trial function, why do we get garbage if we include enough terms that the peak is sharp? It must therefore be important to consider the origin, but how do we give some meaning to the derivative of the absolute value function? The key, supplied when asking in office hours for the course, is to express the absolute value function in terms of Heavyside step functions, for which the derivative can be identified as the delta function.

Correcting, treating the origin this way.

Here’s how we can express the absolute value function using the Heavyside step

where the step function is zero for as plotted in figure (\ref{fig:stepFunction}).

\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{stepFunction}
\caption{stepFunction}
\end{figure}

Expressed this way, with the identification , we have for the derivative of the absolute value function

Observe that we have our expected unit derivative for , and derivative for . At the origin our contributions vanish, and we are left with

We’ve got zero times infinity here, so how do we give meaning to this? As with any delta functional, we’ve got to apply it to a well behaved (square integrable) test function and integrate. Doing so we have

This equals zero for any well behaved test function . Since the delta function only picks up the contribution at the origin, we can therefore identify as zero at the origin.

Using the same technique, we can express our trial function in terms of steps

This we can now take derivatives of, even at the origin, and find

Taking second derivatives we find

Now application of the Hamiltonian operator on our trial function gives us

so

Normalized we have

This is looking much more promising. We’ll have the sign alternation that we require to find a positive, non-complex, value for when is minimized. That is

so the extremum is found at

Plugging this back in we find that our trial function associated with the minimum energy (unnormalized still) is

and that energy, after substitution, is

We have something that’s the true ground state energy, but is at least a ball park value. However, to get this result, we have to be very careful to treat our point of singularity. A derivative that we’d call undefined in first year calculus, is not only defined, but required, for this treatment to work!

My submission for PHY356 (Quantum Mechanics I) Problem Set 5.

[Click here for a PDF of this post with nicer formatting]

Grading notes.

The pdf version above has been adjusted after seeing the comments from the grading. [Click here for the PDF for the original submission, as found below, uncorrected.

Problem.

Statement

A particle of mass m moves along the x-direction such that . Is the state

where is given by Eq. (9.60), is a constant, and time , an energy eigenstate of the system? What is probability per unit length for measuring the particle at position at ? Explain the physical meaning of the above results.

Solution

Is this state an energy eigenstate?

Recall that , , and . With this variable substitution Schr\”{o}dinger’s equation for this harmonic oscillator potential takes the form

While we can blindly substitute a function of the form into this to get

and formally make the identification , this isn’t a normalizable wavefunction, and has no physical relevance, unless we set .

By changing the problem, this state could be physically relevant. We’d require a potential of the form

latex x < a$} \\ \frac{1}{{2}} K x^2 & \quad \mbox{if $latex a < x b$} \\ \end{array}\right.\end{aligned} \hspace{\stretch{1}}(2.3)$

For example, , for constant . For such a potential, within the harmonic well, a general solution of the form

is possible since normalization would not prohibit non-zero values in that situation. For the wave function to be a physically relevant, we require it to be (absolute) square integrable, and must also integrate to unity over the entire interval.

Probability per unit length at .

We cannot answer the question for the probability that the particle is found at the specific position at (that probability is zero in a continuous space), but we can answer the question for the probability that a particle is found in an interval surrounding a specific point at this time. By calculating the average of the probability to find the particle in an interval, and dividing by that interval’s length, we arrive at plausible definition of probability per unit length for an interval surrounding

latex x = x_0$} =\lim_{\epsilon \rightarrow 0} \frac{1}{{\epsilon}} \int_{x_0 – \epsilon/2}^{x_0 + \epsilon/2} {\left\lvert{ \Psi(x, t_0) }\right\rvert}^2 dx = {\left\lvert{\Psi(x_0, t_0)}\right\rvert}^2\end{aligned} \hspace{\stretch{1}}(2.5)$

By this definition, the probability per unit length is just the probability density itself, evaluated at the point of interest.

Physically, for an interval small enough that the probability density is constant in magnitude over that interval, this probability per unit length times the length of this small interval, represents the probability that we will find the particle in that interval.

Probability per unit length for the non-normalizable state given.

It seems possible, albeit odd, that this question is asking for the probability per unit length for the non-normalizable wavefunction 2.1. Since normalization requires , that probability density is simply zero (or undefined, depending on one’s point of view).

Probability per unit length for some more interesting harmonic oscillator states.

Suppose we form the wavefunction for a superposition of all the normalizable states

Here it is assumed that the coefficients yield unit probability

For the impure state of 2.6 we have for the probability density

Evaluation at the point , we have

It is interesting that the probability per unit length only has time dependence for a mixed state.

For a pure state and its wavefunction we have just

This is zero for odd . For even is appears that may equal (this is true at least up to n=4). If that’s the case, we have for non-mixed states, with even numbered energy quantum numbers, at a probability per unit length value of .