Exponential solutions to second order linear system

[Click here for a PDF of this post with nicer formatting (especially if my latex to wordpress script has left FORMULA DOES NOT PARSE errors.)]

Motivation

We’re discussing specific forms to systems of coupled linear differential equations, such as a loop of “spring” connected masses (i.e. atoms interacting with harmonic oscillator potentials) as sketched in fig. 1.1.

Fig 1.1: Three springs loop

 

Instead of assuming a solution, let’s see how far we can get attacking this problem systematically.

Matrix methods

Suppose that we have a set of masses constrained to a circle interacting with harmonic potentials. The Lagrangian for such a system (using modulo indexing) is

The force equations follow directly from the Euler-Lagrange equations

For the simple three particle system depicted above, this is

with equations of motion

Let’s partially non-dimensionalize this. First introduce average mass and spring constants , and rearrange slightly

With

Our system takes the form

We can at least theoretically solve this in a simple fashion if we first convert it to a first order system. We can do that by augmenting our vector of displacements with their first derivatives

So that

Now the solution is conceptually trivial

We are however, faced with the task of exponentiating the matrix . All the powers of this matrix will be required, but they turn out to be easy to calculate

allowing us to write out the matrix exponential

Case I: No zero eigenvalues

Provided that has no zero eigenvalues, we could factor this as

This initially leads us to believe the following, but we’ll find out that the three springs interaction matrix does have a zero eigenvalue, and we’ll have to be more careful. If there were any such interaction matrices that did not have such a zero we could simply write

This is

The solution, written out is

so that

As a check differentiation twice shows that this is in fact the general solution, since we have

and

Observe that this solution is a general solution to second order constant coefficient linear systems of the form we have in eq. 1.5. However, to make it meaningful we do have the additional computational task of performing an eigensystem decomposition of the matrix . We expect negative eigenvalues that will give us oscillatory solutions (ie: the matrix square roots will have imaginary eigenvalues).

Example: An example diagonalization to try things out

{example:threeSpringLoop:1}{

Let’s do that diagonalization for the simplest of the three springs system as an example, with and , so that we have

A orthonormal eigensystem for is

With

We have

We also find that and its root are intimately related in a surprising way

We also see, unfortunately that has a zero eigenvalue, so we can’t compute . We’ll have to back and up and start again differently.
}

Case II: allowing for zero eigenvalues

Now that we realize we have to deal with zero eigenvalues, a different approach suggests itself. Instead of reducing our system using a Hamiltonian transformation to a first order system, let’s utilize that diagonalization directly. Our system is

where and

Let

so that our system is just

or

This is equations, each decoupled and solvable by inspection. Suppose we group the eigenvalues into sets . Our solution is then

Transforming back to lattice coordinates using , we have

We see that the zero eigenvalues integration terms have no contribution to the lattice coordinates, since , for all .

If are a set of not necessarily orthonormal eigenvectors for , then the vectors , where are the reciprocal frame vectors. These can be extracted from (i.e., the rows of ). Taking dot products between with and , provides us with the unknown coefficients

Supposing that we constrain ourself to looking at just the oscillatory solutions (i.e. the lattice does not shake itself to pieces), then we have

Eigenvectors for eigenvalues that were degenerate have been explicitly enumerated here, something previously implied. Observe that the dot products of the form have been put into projector operator form to group terms more nicely. The solution can be thought of as a weighted projector operator working as a time evolution operator from the initial state.

Example: Our example interaction revisited

{example:threeSpringLoop:2}{

Recall that we had an orthonormal basis for the eigensubspace for the interaction example of eq. 1.20 again, so . We can sum to find

The leading matrix is an orthonormal projector of the initial conditions onto the eigen subspace for . Observe that this is proportional to itself, scaled by the square of the non-zero eigenvalue of . From this we can confirm by inspection that this is a solution to , as desired.
}

Fourier transform methods

Let’s now try another item from our usual toolbox on these sorts of second order systems, the Fourier transform. For a one variable function of time let’s write the transform pair as

One mass harmonic oscillator

The simplest second order system is that of the harmonic oscillator

Application of the transform gives

We clearly have a constraint that is a function of frequency, but one that has to hold for all time. Let’s transform this constraint to the frequency domain to consider that constraint independent of time.

How do we make sense of this?

Since is an integration variable, we can’t just mandate that it equals the constant driving frequency . It’s clear that we require a constraint on the transform as well. As a trial solution, imagine that

latex \left\lvert {\omega – \pm \omega_\circ} \right\rvert < \omega_{\text{cutoff}}$} \\ 0 & \quad \mbox{otherwise}\end{array}\right.\end{aligned} \hspace{\stretch{1}}(1.0.35.35)$

This gives us

Now it is clear that we can satisfy our constraint only if the interval is made infinitesimal. Specifically, we require both a constraint and that the transform have a delta function nature. That is

Substitution back into our transform gives

We can verify quickly that this satisfies our harmonic equation .

Two mass harmonic oscillator

Having applied the transform technique to the very simplest second order system, we can now consider the next more complex system, that of two harmonically interacting masses (i.e. two masses on a frictionless spring).

F1

Our system is described by

and the pair of Euler-Lagrange equations

The equations of motion are

Let

Insertion of these transform pairs into our equations of motion produces a pair of simultaneous integral equations to solve

As with the single spring case, we can decouple these equations with an inverse transformation operation , which gives us (after dropping primes)

Taking determinants gives us the constraint on the frequency

Introducing a reduced mass

the pair of solutions are

As with the single mass oscillator, we require the functions to also be expressed as delta functions. The frequency constraint and that delta function requirement together can be expressed, for as

With a transformation back to time domain, we have functions of the form

Back insertion of these into the equations of motion, we have

Equality requires identity for all powers of , or

or and

Observe that

(with a similar alternate result). We can rewrite eq. 1.0.35.35 as

It’s clear that there’s two pairs of linear dependencies here, so the determinant is zero as expected. We can read off the remaining relations. Our undetermined coefficients are given by

Observe that the constant term is not really of interest, since it represents a constant displacement of both atoms (just a change of coordinates).

Check:

Reflection

We’ve seen that we can solve any of these constant coefficient systems exactly using matrix methods, however, these will not be practical for large systems unless we have methods to solve for all the non-zero eigenvalues and their corresponding eigenvectors. With the Fourier transform methods we find that our solutions in the frequency domain is of the form

or in the time domain

We assumed exactly this form of solution in class. The trial solution that we used in class factored out a phase shift from of the form of , but that doesn’t change the underling form of that assumed solution. We have however found a good justification for the trial solution we utilized.

An updated compilation of notes, for ‘PHY452H1S Basic Statistical Mechanics’, Taught by Prof. Arun Paramekanti

Here’s my second update of my notes compilation for this course, including all of the following:

March 27, 2013 Fermi gas

March 26, 2013 Fermi gas thermodynamics

March 26, 2013 Fermi gas thermodynamics

March 23, 2013 Relativisitic generalization of statistical mechanics

March 21, 2013 Kittel Zipper problem

March 18, 2013 Pathria chapter 4 diatomic molecule problem

March 17, 2013 Gibbs sum for a two level system

March 16, 2013 open system variance of N

March 16, 2013 probability forms of entropy

March 14, 2013 Grand Canonical/Fermion-Bosons

March 13, 2013 Quantum anharmonic oscillator

March 12, 2013 Grand canonical ensemble

March 11, 2013 Heat capacity of perturbed harmonic oscillator

March 10, 2013 Langevin small approximation

March 10, 2013 Addition of two one half spins

March 10, 2013 Midterm II reflection

March 07, 2013 Thermodynamic identities

March 06, 2013 Temperature

March 05, 2013 Interacting spin

plus everything detailed in the description of my first update and before.

Addition of two one half spins

[Click here for a PDF of this post with nicer formatting (especially if my latex to wordpress script has left FORMULA DOES NOT PARSE errors.)]

In class an example of interacting spin was given where the Hamiltonian included a two spins dot product

The energy eigenvalues for this Hamiltonian were derived by using the trick to rewrite this in terms of just squared spin operators

For each of these terms we can calculate the total energy eigenvalues from

where takes on the values of the total spin for the (possibly composite) spin operator. Thinking about the spin operators in their matrix representation, it’s not obvious to me that we can just add the total spins, so that if and are the spin operators for two respective particle, then the total system has a spin operator (really , since the respective spin operators only act on their respective particles).

Let’s develop a bit of intuition on this, by calculating the energy eigenvalues of using Pauli matrices.

First lets look at how each of the Pauli matrices operate on the eigenvectors

Summarizing, these are

For convienience let’s avoid any sort of direct product notation, with the composite operations defined implicitly by

Now let’s compute all the various operations

Tabulating first the action of the sum of the and operators we have

so that

Now we are set to write out the Hamiltonian matrix. Doing this with respect to the basis , we have

Two of the eigenvalues we can read off by inspection, and for the other two need to solve

or

These are the last of the triplet energy eigenvalues and the singlet value that we expected from the spin addition method. The eigenvectors for the eigenvalue is given by the solution of

So the eigenvector is

For our eigenvalue we seek

So the eigenvector is

An orthonormal basis with respective eigenvalues is thus given by

Confirmation of spin additivity.

Let’s use this to confirm that for , the two spin particles have a combined spin given by

With

we have for the energy eigenstate of

and for the energy eigenstate of

We get the and eigenvalues respectively as expected.

PHY456H1F: Quantum Mechanics II. Lecture 4 (Taught by Prof J.E. Sipe). Time independent perturbation theory (continued)

[Click here for a PDF of this post with nicer formatting (especially if my latex to wordpress script has left FORMULA DOES NOT PARSE errors.)]

Disclaimer.

Peeter’s lecture notes from class. May not be entirely coherent.

Time independent perturbation.

The setup

To recap, we were covering the time independent perturbation methods from section 16.1 of the text [1]. We start with a known Hamiltonian , and alter it with the addition of a “small” perturbation

For the original operator, we assume that a complete set of eigenvectors and eigenkets is known

We seek the perturbed eigensolution

and assumed a perturbative series representation for the energy eigenvalues in the new system

Given an assumed representation for the new eigenkets in terms of the known basis

and a pertubative series representation for the probability coefficients

so that

Setting requires

for

We rescaled our kets

where

The normalization of the rescaled kets is then

One can then construct a renormalized ket if desired

so that

The meat.

That’s as far as we got last time. We continue by renaming terms in 2.10

where

Now we act on this with the Hamiltonian

or

Expanding this, we have

We want to write this as

This is

So we form

and so forth.

Zeroth order in

Since , this first condition on is not much more than a statement that .

First order in

How about ? For this to be zero we require that both of the following are simultaneously zero

This first condition is

With

or

From the second condition we have

Utilizing the Hermitian nature of we can act backwards on

We note that . We can also expand the , which is

I found that reducing this sum wasn’t obvious until some actual integers were plugged in. Suppose that , and , then this is

More generally that is

Utilizing this gives us

And summarizing what we learn from our conditions we have

Second order in

Doing the same thing for we form (or assume)

We need to know what the is, and find that it is zero

Again, suppose that . Our sum ranges over all , so all the brakets are zero. Utilizing that we have

From 2.34 we have

We can now summarize by forming the first order terms of the perturbed energy and the corresponding kets

We can continue calculating, but are hopeful that we can stop the calculation without doing more work, even if . If one supposes that the

term is “small”, then we can hope that truncating the sum will be reasonable for . This would be the case if

however, to put some mathematical rigor into making a statement of such smallness takes a lot of work. We are referred to [2]. Incidentally, these are loosely referred to as the first and second testaments, because of the author’s name, and the fact that they came as two volumes historically.

References

[1] BR Desai. Quantum mechanics with basic field theory. Cambridge University Press, 2009.

[2] A. Messiah, G.M. Temmer, and J. Potter. Quantum mechanics: two volumes bound as one. Dover Publications New York, 1999.

PHY456H1F, Quantum Mechanics II. My solutions to problem set 1 (ungraded).

[Click here for a PDF of this post with nicer formatting (especially if my latex to wordpress script has left FORMULA DOES NOT PARSE errors.)]

Harmonic oscillator.

Consider

Since it’s been a while let’s compute the raising and lowering factorization that was used so extensively for this problem.

It was of the form

Why this factorization has an imaginary in it is a good question. It’s not one that is given any sort of rationale in the text ([1]).

It’s clear that we want and . The difference is then

That commutator is an value, but what was the sign? Let’s compute so we don’t get it wrong

So we have

Factoring out an produces the form of the Hamiltonian that we used before

The factors were labeled the uppering () and lowering () operators respectively, and written

Observe that we can find the inverse relations

Question
What is a good reason that we chose this particular factorization? For example, a quick computation shows that we could have also picked

I don’t know that answer. That said, this second factorization is useful in that it provides the commutator relation between the raising and lowering operators, since subtracting 1.11 and 1.6 yields

If we suppose that we have eigenstates for the operator of the form

then the problem of finding the eigensolution of reduces to solving this problem. Because commutes with , an eigenstate of is also an eigenstate of . Utilizing 1.12 we then have

so we see that is an eigenstate of with eigenvalue .

Similarly for the raising operator

and find that is also an eigenstate of with eigenvalue .

Supposing that there is a lowest energy level (because the potential has a lower bound of zero) then the state for which the energy is the lowest when operated on by we have

Thus

and

This seems like a small bit of slight of hand, since it sneakily supplies an integer value to where up to this point was just a label.

If the eigenvalue equation we are trying to solve for the Hamiltonian is

Then we must then have

Part (a)

We’ve now got enough context to attempt the first part of the question, calculation of

We’ve calculated things like this before, such as

To continue we need an exact relation between and . Recall that was an eigenstate of with eigenvalue . This implies that the eigenstates and are proportional

or

so that

Similarly let

or

so that

We can now return to 1.19, and find

Consider half of this braket

Squaring, utilizing the Hermitian nature of the operator

Part (b)

Find the ground state energy of the Hamiltonian for .

The new Hamiltonian has the form

where

The energy states of the Hamiltonian are thus

and the ground state of the modified Hamiltonian is thus

Part (c)

Find the ground state energy of the Hamiltonian .

With a bit of play, this new Hamiltonian can be factored into

where

From 1.29 we see that we have the same sort of commutator relationship as in the original Hamiltonian

and because of this, all the preceding arguments follow unchanged with the exception that the energy eigenstates of this Hamiltonian are shifted by a constant

where the states are simultaneous eigenstates of the operator

The ground state energy is then

This makes sense. A translation of the entire position of the system should not effect the energy level distribution of the system, but we have set our reference potential differently, and have this constant energy adjustment to the entire system.

Hydrogen atom and spherical harmonics.

We are asked to show that for any eigenkets of the hydrogen atom we have

The summary sheet provides us with the wavefunction

where is a real valued function defined in terms of Lagueere polynomials. Working with the expectation of the operator to start with we have

Recalling that the only dependence in is we can perform the integration directly, which is

We have the same story for the expectation which is

Our integral is then just

also zero. The expectation is a slightly different story. There we have

Within this last integral we can make the substitution

and the integral takes the form

Here we have the product of two even functions, times one odd function (), over a symmetric interval, so the end result is zero, completing the problem.

I wasn’t able to see how to exploit the parity result suggested in the problem, but it wasn’t so bad to show these directly.

Angular momentum operator.

Working with the appropriate expressions in Cartesian components, confirm that for each component of angular momentum , if is in fact only a function of .

In order to proceed, we will have to consider a matrix element, so that we can operate on in position space. For that matrix element, we can proceed to insert complete states, and reduce the problem to a question of wavefunctions. That is

With we have

We are left with an sum of a symmetric product with the antisymmetric tensor so this is zero for all .

References

[1] BR Desai. Quantum mechanics with basic field theory. Cambridge University Press, 2009.

Lorentz Force Trajectory.

Solving the Lorentz force equation in the non-relativistic limit.

The problem.

[1] treats the solution of the Lorentz force equation in covariant form. Let’s try this for non-relativistic motion for constant fields, but without making the usual assumptions about perpendicular electric and magnetic fields, or alignment of the axis. Our equation to solve is

so in the non-relativistic limit we want to solve the matrix equation

First attempt.

This is very much like the plain old LDE

which we can solve using integrating factors

This we can rearrange and integrate to find a solution to the non-homogeneous problem

This solution to the non-homogeneous equation is thus

Because this already incorporates the homogeneous solution , this is also the general form of the solution.

Can we do something similar for the matrix equation of 1.2? It is tempting to try, rearranging in the same way like so

Our matrix exponentials are perfectly well formed, but we will run into trouble attempting this. We can get as far as the integral above before running into trouble

Only when do we have

but in our case, this determinant is zero, due to the antisymmetry that is built into our magnetic field tensor. It appears that we need a different strategy.

Second attempt.

It’s natural to attempt to pull out our spectral theorem toolbox. We find three independent eigenvalues for our matrix (one of which is naturally zero due to the singular nature of the matrix).

These eigenvalues are

The corresponding orthonormal eigenvectors are found to be

The last pair of eigenvectors are computed with the assumption that not both of and are zero. This allows for the spectral decomposition

We can use this to decouple our equation

forming instead

Written out explicitly, this is a set of three independent equations

Utilizing 1.6 our solution is

Reinserting matrix form we have

with

We have

Observe that the dot products embedded here can be nicely expressed in terms of the eigenvectors since

Our solution is thus a weighted sum of projections of the electric field vector onto the eigenvectors formed strictly from the magnetic field tensor

Recalling that , the unit vector that lies in the direction of the magnetic field, we have

Also observe that this is a manifestly real valued solution since remaining eigenvectors are conjugate pairs as are the differential solutions . This leaves us with

It is natural to express in terms of the direction cosines of the magnetic field vector

Is there a way to express this beastie in a coordinate free fashion? I experimented with this a bit looking for something that would provide some additional geometrical meaning but did not find it. Further play with that is probably something for another day.

What we do see is that our velocity has two main components, one of which is linearly increasing in proportion to the colinearity of the magnetic and electric fields. The other component is oscillatory. With a better geometrical description of that eigenvector we could perhaps understand the mechanics a bit better.

References

[1] C. Doran and A.N. Lasenby. Geometric algebra for physicists. Cambridge University Press New York, Cambridge, UK, 1st edition, 2003.

PHY450H1S (relativistic electrodynamics) Problem Set 3.

[Click here for a PDF of this post with nicer formatting]

Disclaimer.

This problem set is as yet ungraded (although only the second question will be graded).

Problem 1. Fun with , , , and the duality of Maxwell’s equations in vacuum.

1. Statement. rank 3 spatial antisymmetric tensor identities.

Prove that

and use it to find the familiar relation for

Also show that

(Einstein summation implied all throughout this problem).

1. Solution

We can explicitly expand the (implied) sum over indexes . This is

For any only one term is non-zero. For example with , we have just a contribution from the part of the sum

The value of this for is

whereas for we have

Our sum has value one when matches , and value minus one for when are permuted. We can summarize this, by saying that when we have

However, observe that when the RHS is

as desired, so this form works in general without any qualifier, completing this part of the problem.

This gives us

We have one more identity to deal with.

We can expand out this (implied) sum slow and dumb as well

Now, observe that for any only one term of this sum is picked up. For example, with no loss of generality, pick . We are left with only

This has the value

when and is zero otherwise. We can therefore summarize the evaluation of this sum as

completing this problem.

2. Statement. Determinant of three by three matrix.

Prove that for any matrix : and that .

2. Solution

In class Simon showed us how the first identity can be arrived at using the triple product . It occurred to me later that I’d seen the identity to be proven in the context of Geometric Algebra, but hadn’t recognized it in this tensor form. Basically, a wedge product can be expanded in sums of determinants, and when the dimension of the space is the same as the vector, we have a pseudoscalar times the determinant of the components.

For example, in 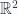, let’s take the wedge product of a pair of vectors. As preparation for the relativistic 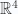case We won’t require an orthonormal basis, but express the vector in terms of a reciprocal frame and the associated components

where

When we get to the relativistic case, we can pick (but don’t have to) the standard basis

for which our reciprocal frame is implicitly defined by the metric

Anyways. Back to the problem. Let’s examine the 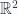case. Our wedge product in coordinates is

Since there are only two basis vectors we have

Our wedge product is a product of the determinant of the vector coordinates, times the 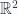pseudoscalar .

This doesn’t look quite like the 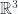relation that we want to prove, which had an antisymmetric tensor factor for the determinant. Observe that we get the determinant by picking off the component of the bivector result (the only component in this case), and we can do that by dotting with . To get an antisymmetric tensor times the determinant, we have only to dot with a different pseudoscalar (one that differs by a possible sign due to permutation of the indexes). That is

Now, if we write and we have

We can write this in two different ways. One of which is

and the other of which is by introducing free indexes for and , and summing antisymmetrically over these. That is

So, we have

This result hold regardless of the metric for the space, and does not require that we were using an orthonormal basis. When the metric is Euclidean and we have an orthonormal basis, then all the indexes can be dropped.

The 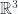and 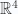cases follow in exactly the same way, we just need more vectors in the wedge products.

For the 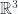case we have

Again, with and , and we have

and we can choose to write this in either form, resulting in the identity

The case follows exactly the same way, and we have

This time with and , and , and we have

This one is almost the identity to be established later in problem 1.4. We have only to raise and lower some indexes to get that one. Note that in the Minkowski standard basis above, because must be a permutation of for a non-zero result, we must have

So raising and lowering the identity above gives us

No sign changes were required for the indexes , since they are paired.

Until we did the raising and lowering operations here, there was no specific metric required, so our first result 2.33 is the more general one.

There’s one more part to this problem, doing the antisymmetric sums over the indexes . For the case we have

We conclude that

For the case we have the same operation

So we conclude

It’s clear what the pattern is, and if we evaluate the sum of the antisymmetric tensor squares in we have

So, for our SR case we have

This was part of question 1.4, albeit in lower index form. Here since all indexes are matched, we have the same result without major change

The main difference is that we are now taking the determinant of a lower index tensor.

3. Statement. Rotational invariance of 3D antisymmetric tensor

Use the previous results to show that is invariant under rotations.

3. Solution

We apply transformations to coordinates (and thus indexes) of the form

With our tensor transforming as its indexes, we have

We’ve got 2.32, which after dropping indexes, because we are in a Euclidean space, we have

Let , which gives us

but since , we have shown that is invariant under rotation.

4. Statement. Rotational invariance of 4D antisymmetric tensor

Use the previous results to show that is invariant under Lorentz transformations.

4. Solution

This follows the same way. We assume a transformation of coordinates of the following form

where the determinant of (sanity check of sign: ).

Our antisymmetric tensor transforms as its coordinates individually

Let , and raise and lower all the indexes in 2.46 for

We have

Since both are therefore invariant under Lorentz transformation.

5. Statement. Sum of contracting symmetric and antisymmetric rank 2 tensors

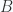Show that if is symmetric and is antisymmetric.

5. Solution

We swap indexes in 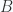, switch dummy indexes, then swap indexes in

Our result is the negative of itself, so must be zero.

6. Statement. Characteristic equation for the electromagnetic strength tensor

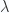Show that is invariant under Lorentz transformations. Consider the polynomial of , also called the characteristic polynomial of the matrix . Find the coefficients of the expansion of in powers of in terms of the components of . Use the result to argue that and are Lorentz invariant.

6. Solution

The invariance of the determinant

Let’s consider how any lower index rank 2 tensor transforms. Given a transformation of coordinates

where , and . Let’s reflect briefly on why this determinant is unit valued. We have

which implies that the transformation product is

the identity matrix. The identity matrix has unit determinant, so we must have

Since we have

which is all that we can say about the determinant of this class of transformations by considering just invariance. If we restrict the transformations of coordinates to those of the same determinant sign as the identity matrix, we rule out reflections in time or space. This seems to be the essence of the labeling.

Why dwell on this? Well, I wanted to be clear on the conventions I’d chosen, since parts of the course notes used , and , and gave that matrix unit determinant. That looks like it is equivalent to my , except that the one in the course notes is loose when it comes to lower and upper indexes since it gives .

I’ll write

and require this (not ) to be the matrix with unit determinant. Having cleared the index upper and lower confusion I had trying to reconcile the class notes with the rules for index manipulation, let’s now consider the Lorentz transformation of a lower index rank 2 tensor (not necessarily antisymmetric or symmetric)

We have, transforming in the same fashion as a lower index coordinate four vector (but twice, once for each index)

The determinant of the transformation tensor is

We see that the determinant of a lower index rank 2 tensor is invariant under Lorentz transformation. This would include our characteristic polynomial .

Expanding the determinant.

Utilizing 2.39 we can now calculate the characteristic polynomial. This is

However, , or . This means we have

and our determinant is reduced to

If we expand this out we have our powers of 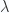coefficients are

By 2.39 the coefficient is just .

The terms can be seen to be zero. For example, the first one is

where the final equality to zero comes from summing a symmetric and antisymmetric product.

Similarly the 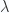coefficients can be shown to be zero. Again the first as a sample is

Disregarding the factor, let’s just expand this antisymmetric sum

Of the two terms above that were retained, they are the only ones without a zero factor. Consider the first part of this remaining part of the sum. Employing the metric tensor, to raise indexes so that the antisymmetry of can be utilized, and then finally relabeling all the dummy indexes we have

This is just the negative of the second term in the sum, leaving us with zero.

Finally, we have for the coefficient ()

Therefore, our characteristic polynomial is

Observe that in matrix form our strength tensors are

From these we can compute easily by inspection

Computing the determinant is not so easy. The dumb and simple way of expanding by cofactors takes two pages, and yields eventually

That supplies us with a relation for the characteristic polynomial in and

Observe that we found this for the special case where and were perpendicular in homework 2. Observe that when we have that perpendicularity, we can solve for the eigenvalues by inspection

and were able to diagonalize the matrix to solve the Lorentz force equation in parametric form. When we had real eigenvalues and an orthogonal diagonalization when . For the , we had a two purely imaginary eigenvalues, and when this was a Hermitian diagonalization. For the general case, when one of , or was zero, things didn’t have the same nice closed form solution.

In general our eigenvalues are

For the purposes of this problem we really only wish to show that and are Lorentz invariants. When we have , a Lorentz invariant. This must mean that is itself a Lorentz invariant. Since that is invariant, and we require to be invariant for any other possible values of 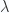, the difference must also be Lorentz invariant.

7. Statement. Show that the pseudoscalar invariant has only boundary effects.

Use integration by parts to show that only depends on the values of at the “boundary” of spacetime (e.g. the “surface” depicted on page 105 of the notes) and hence does not affect the equations of motion for the electromagnetic field.

7. Solution

This proceeds in a fairly straightforward fashion

Now, observe that by the Bianchi identity, this second term is zero

Now we have a set of perfect differentials, and can integrate

We are left with a only contributions to the integral from the boundary terms on the spacetime hypervolume, three-volume normals bounding the four-volume integration in the original integral.

8. Statement. Electromagnetic duality transformations.

Show that the Maxwell equations in vacuum are invariant under the transformation: , where is the dual electromagnetic stress tensor. Replacing 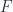with is known as “electric-magnetic duality”. Explain this name by considering the transformation in terms of and . Are the Maxwell equations with sources invariant under electric-magnetic duality transformations?

8. Solution

Let’s first consider the explanation of the name. First recall what the expansions are of and in terms of and . These are

with , and .

The magnetic field components are

with and .

Now let’s expand the dual tensors. These are

and

Summarizing we have

Is there a sign error in the result? Other than that we have the same sort of structure for the tensor with 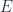and 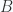switched around.

Let’s write these in matrix form, to compare

From these we can see by inspection that we have

This is consistent with the stated result in [1] (except for a factor of due to units differences), so it appears the signs above are all kosher.

Now, let’s see if the if the dual tensor satisfies the vacuum equations.

So the first checks out, provided we have no sources. If we have sources, then we see here that Maxwell’s equations do not hold since this would imply that the four current density must be zero.

How about the Bianchi identity? That gives us

The factor of two is slightly curious. Is there a mistake above? If there is a mistake, it doesn’t change the fact that Maxwell’s equation

Gives us zero for the Bianchi identity under source free conditions of .

Problem 2. Transformation properties of and , again.

1. Statement

Use the form of from page 82 in the class notes, the transformation law for given further down that same page, and the explicit form of the matrix (say, corresponding to motion in the positive direction with speed ) to derive the transformation law of the fields and . Use the transformation law to find the electromagnetic field of a charged particle moving with constant speed in the positive direction and check that the result agrees with the one that you obtained in Homework 2.

1. Solution

Given a transformation of coordinates

our rank 2 tensor transforms as

Introducing matrices

and noting that , we can express the electromagnetic strength tensor transformation as

The class notes use , which violates our conventions on mixed upper and lower indexes, but the end result 3.80 is the same.

Writing

we can compute the transformed field strength tensor

As a check we have the antisymmetry that is expected. There is also a regularity to the end result that is aesthetically pleasing, hinting that things are hopefully error free. In coordinates for and this is

Writing , we have

which puts us enroute to a tidier vector form

For a vector , write , , allowing a compact description of the field transformation

Now, we want to consider the field of a moving particle. In the particle’s (unprimed) rest frame the field due to its potential is

Coordinates for a “stationary” observer, who sees this particle moving along the x-axis at speed are related by a boost in the 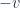direction

Therefore the fields in the observer frame will be

More explicitly with this is

Comparing to Problem 3 in Problem set 2, I see that this matches the result obtained by separately transforming the gradient, the time partial, and the scalar potential. Actually, if I am being honest, I see that I made a sign error in all the coordinates of when I initially did (this ungraded problem) in problem set 2. That sign error should have been obvious by considering the case which would have mysteriously resulted in inversion of all the coordinates of the observed electric field.

2. Statement

A particle is moving with velocity in perpendicular and fields, all given in some particular “stationary” frame of reference.

\begin{enumerate}
\item Show that there exists a frame where the problem of finding the particle trajectory can be reduced to having either only an electric or only a magnetic field.
\item Explain what determines which case takes place.
\item Find the velocity of that frame relative to the “stationary” frame.
\end{enumerate}

2. Solution

\paragraph{Part 1 and 2:} Existence of the transformation.

In the single particle Lorentz trajectory problem we wish to solve

which in matrix form we can write as

where we write our column vector proper velocity as . Under transformation of coordinates , with , this becomes

Suppose we can find eigenvectors for the matrix . That is for some eigenvalue 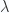, we can find an eigenvector

Rearranging we have

and conclude that lies in the null space of the matrix and that this difference of matrices must have a zero determinant

Since for any Lorentz transformation in , and we have

In problem 1.6, we called this our characteristic equation . Observe that the characteristic equation is Lorentz invariant for any 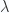, which requires that the eigenvalues 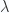are also Lorentz invariants.

In problem 1.6 of this problem set we computed that this characteristic equation expands to

The eigenvalues for the system, also each necessarily Lorentz invariants, are

Observe that in the specific case where , as in this problem, we must have in all frames, and the two non-zero eigenvalues of our characteristic polynomial are simply

These and are the invariants for this system. If we have in one frame, we must also have in another frame, still maintaining perpendicular fields. In particular if we maintain real eigenvalues. Similarly if in some frame, we must always have imaginary eigenvalues, and this is also true in the case.

While the problem can be posed as a pure diagonalization problem (and even solved numerically this way for the general constant fields case), we can also work symbolically, thinking of the trajectories problem as simply seeking a transformation of frames that reduce the scope of the problem to one that is more tractable. That does not have to be the linear transformation that diagonalizes the system. Instead we are free to transform to a frame where one of the two fields or is zero, provided the invariants discussed are maintained.

\paragraph{Part 3:} Finding the boost velocity that wipes out one of the fields.

Let’s now consider a Lorentz boost , and seek to solve for the boost velocity that wipes out one of the fields, given the invariants that must be maintained for the system

To make things concrete, suppose that our perpendicular fields are given by and .

Let also assume that we can find the velocity for which one or more of the transformed fields is zero. Suppose that velocity is

where are the direction cosines of so that . We will want to compute the components of and parallel and perpendicular to this velocity.

Those are

For the magnetic field we have

and

Now, observe that , but this is just zero. So we have . So our cross products terms are just

We can now express how the fields transform, given this arbitrary boost velocity. From 3.97, this is

Zero Electric field case.

Let’s tackle the two cases separately. First when , we can transform to a frame where . In coordinates from 3.117 this supplies us three sets of equations. These are

With an assumed solution the 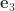coordinate equation implies that one of 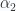or is zero. Perhaps there are solutions with too, but inspection shows that nicely kills off the first equation. Since , that also implies that we are left with

Or

Our velocity was solving the problem for the case up to an adjustable constant . That constant comes with constraints however, since we must also have our cosine . Expressed another way, the magnitude of the boost velocity is constrained by the relation

It appears we may also pick the equality case, so one velocity (not unique) that should transform away the electric field is

This particular boost direction is perpendicular to both fields. Observe that this highlights the invariance condition since we see this is required for a physically realizable velocity. Boosting in this direction will reduce our problem to one that has only the magnetic field component.

Zero Magnetic field case.

Now, let’s consider the case where we transform the magnetic field away, the case when our characteristic polynomial has strictly real eigenvalues . In this case, if we write out our equations for the transformed magnetic field and require these to separately equal zero, we have

Similar to before we see that kills off the first and second equations, leaving just

We now have a solution for the family of direction vectors that kill the magnetic field off

In addition to the initial constraint that , we have as before, constraints on the allowable values of

Like before we can pick the equality , yielding a boost direction of

Again, we see that the invariance condition is required for a physically realizable velocity if that velocity is entirely perpendicular to the fields.

Problem 3. Continuity equation for delta function current distributions.

Statement

Show explicitly that the electromagnetic 4-current for a particle moving with constant velocity (considered in class, p. 100-101 of notes) is conserved . Give a physical interpretation of this conservation law, for example by integrating over some spacetime region and giving an integral form to the conservation law ( is known as the “continuity equation”).

Solution

First lets review. Our four current was defined as

If each of the trajectories represents constant motion we have

The spacetime split of this four vector is

with differentials

Writing out the delta functions explicitly we have

So our time and space components of the current can be written

Each of these integrals can be evaluated with respect to the time coordinate delta function leaving the distribution

With this more general expression (multi-particle case) it should be possible to show that the four divergence is zero, however, the problem only asks for one particle. For the one particle case, we can make things really easy by taking the initial point in space and time as the origin, and aligning our velocity with one of the coordinates (say ).

Doing so we have the result derived in class

Our divergence then has only two portions

and these cancel out when summed. Note that this requires us to be loose with our delta functions, treating them like regular functions that are differentiable.

For the more general multiparticle case, we can treat the sum one particle at a time, and in each case, rotate coordinates so that the four divergence only picks up one term.

As for physical interpretation via integral, we have using the four dimensional divergence theorem

where is the three-volume element perpendicular to a plane. These volume elements are detailed generally in the text [2], however, they do note that one special case specifically , the element of the three-dimensional (spatial) volume “normal” to hyperplanes .

Without actually computing the determinants, we have something that is roughly of the form

This is cheating a bit to just write . Are there specific orientations required by the metric. To be precise we’d have to calculate the determinants detailed in the text, and then do the duality transformations.

Per unit time, we can write instead

Rather loosely this appears to roughly describe that the rate of change of charge in a volume must be matched with the “flow” of current through the surface within that amount of time.

References

[1] Wikipedia. Electromagnetic tensor — wikipedia, the free encyclopedia [online]. 2011. [Online; accessed 27-February-2011]. http://en.wikipedia.org/w/index.php?title=Electromagnetic_tensor&oldid=414989505.

[2] L.D. Landau and E.M. Lifshitz. The classical theory of fields. Butterworth-Heinemann, 1980.

A problem on spherical harmonics.

[Click here for a PDF of this post with nicer formatting]

Motivation.

One of the PHY356 exam questions from the final I recall screwing up on, and figuring it out after the fact on the drive home. The question actually clarified a difficulty I’d had, but unfortunately I hadn’t had the good luck to perform such a question, to help figure this out before the exam.

From what I recall the question provided an initial state, with some degeneracy in , perhaps of the following form

and a Hamiltonian of the form

From what I recall of the problem, I am going to reattempt it here now.

Evolved state.

One part of the question was to calculate the evolved state. Application of the time evolution operator gives us

Now we note that , and , so the exponentials reduce this nicely to just

Probabilities for measurement outcomes.

I believe we were also asked what the probabilities for the outcomes of a measurement of at this time would be. Here is one place that I think that I messed up, and it is really a translation error, attempting to get from the english description of the problem to the math description of the same. I’d had trouble with this process a few times in the problems, and managed to blunder through use of language like “measure”, and “outcome”, but don’t think I really understood how these were used properly.

What are the outcomes that we measure? We measure operators, but the result of a measurement is the eigenvalue associated with the operator. What are the eigenvalues of the operator? These are the values, from the operation . So, given this initial state, there are really two outcomes that are possible, since we have two distinct eigenvalues. These are and for , and respectively.

A measurement of the “outcome” , will be the probability associated with the amplitude (ie: the absolute square of this value). That is

Now, the only other outcome for a measurement of for this state is a measurement of , and the probability of this is then just . On the exam, I think I listed probabilities for three outcomes, with values respectively, but in retrospect that seems blatently wrong.

Probabilities for measurement outcomes.

What are the probabilities for the outcomes for a measurement of after this? The first question is really what are the outcomes. That’s really a question of what are the possible eigenvalues of that can be measured at this point. Recall that we have

So for a state that has only contributions before the measurement, the eigenvalues that can be observed for the operator are respectively and respectively.

For the case, our probability is , leaving as the probability for measurement of the () eigenvalue. We can compute this two ways, and it seems worthwhile to consider both. This first method makes use of the fact that the operator leaves the state vector intact, but it also seems like a bit of a cheat. Consider instead two possible results of measurement after the observation. When an measurement of is performed our state will be left with only the kets. That is

whereas, when a measurement of is performed our state would then only have the contribution, and would be

We have two possible ways of measuring the eigenvalue for . One is when our state was (, and the resulting state has a component, and the other is after the measurement, where our state is left with a component.

The resulting probability is then a conditional probability result

The result is the same, as expected, but this is likely a more convicing argument.

Some worked problems from old PHY356 exams.

[Click here for a PDF of this post with nicer formatting]

Motivation.

Some of the old exam questions that I did for preparation for the exam I liked, and thought I’d write up some of them for potential future reference.

Questions from the Dec 2007 PHY355H1F exam.

1b. Parity operator.

\paragraph{Q:} If is the parity operator, defined by , where is the eigenket of the position operator with eigenvalue ), and is the momentum operator conjugate to , show (carefully) that .

\paragraph{A:}

Consider the matrix element . This is

We’ve taken advantage of the Hermitian property of and here, and can rearrange for

Since this is true for all and we have

Right multiplication by and rearranging we have

1f. Free particle propagator.

\paragraph{Q:} For a free particle moving in one-dimension, the propagator (i.e. the coordinate representation of the evolution operator),

is given by

\paragraph{A:}

This problem is actually fairly straightforward, but it is nice to work it having had a similar problem set question where we were asked about this time evolution operator matrix element (ie: what it’s physical meaning is). Here we have a concrete example of the form of this matrix operator.

Proceeding directly, we have

which is the desired result. Now, let’s look at how this would be used. We can express our time evolved state using this matrix element by introducing an identity

This gives us

However, note that our free particle wave function at time zero is

So the convolution integral 2.6 does not exist. We likely have to require that the solution be not a pure state, but instead a superposition of a set of continuous states (a wave packet in position or momentum space related by Fourier transforms). That is

The time evolution of this wave packet is then determined by the propagator, and is

or in terms of the position space wave packet evaluated at time zero

We see that the propagator also ends up with a Fourier transform structure, and we have

Does that Fourier transform exist? I’d not be surprised if it ended up with a delta function representation. I’ll hold off attempting to evaluate and reduce it until another day.

4. Hydrogen atom.

This problem deals with the hydrogen atom, with an initial ket

where

etc.

\paragraph{Q: (a)}

If no measurement is made until time ,

what is the ket just before the measurement is made?

\paragraph{A:}

Our time evolved state is

Also observe that this initial time was picked to make the exponential values come out nicely, and we have

so our time evolved state is just

\paragraph{Q: (b)}

Suppose that at time an measurement is made, and the outcome 0 is recorded. What is the appropriate ket right after the measurement?

\paragraph{A:}

A measurement with outcome 0, means that the operator measurement found the state at that point to be the eigenstate for eigenvalue 0. Recall that if is an eigenstate of we have

so a measurement of with outcome zero means that we have . Our measurement of at time therefore filters out all but the states and our new state is proportional to the projection over all states as follows

A final normalization yields

\paragraph{Q: (c)}

Right after this measurement, what is ?

\paragraph{A:}

Our amplitude is

so the probability density is

\paragraph{Q: (d)}

If then a position measurement is made immediately, which if any components of the expectation value of will be nonvanishing? Justify your answer.

\paragraph{A:}

The expectation value of this vector valued operator with respect to a radial state can be expressed as

where .

Consider one of the matrix elements, and expand this by introducing an identity twice

Because our state has only contributions, the only dependence for the and components of come from those components themselves. For , we therefore integrate , and for we integrate , and these terms vanish. Our expectation value for for this state, therefore lies completely on the axis.

Questions from the Dec 2008 PHY355H1F exam.

1b. Trace invariance for unitary transformation.

\paragraph{Q:} Show that the trace of an operator is invariant under unitary transforms, i.e. if , where is a unitary operator, prove .

\paragraph{A:}

The bulk of this question is really to show that commutation of operators leaves the trace invariant (unless this is assumed). To show that we start with the definition of the trace

Thus we have

For the unitarily transformed operator we have

1d. Determinant of an exponential operator in terms of trace.

\paragraph{Q:} If is an Hermitian operator, show that

where the Determinant () of an operator is the product of all its eigenvectors.

\paragraph{A:}

The eigenvalues clue in the question provides the starting point. We write the exponential in its series form

Now, suppose that we have the following eigenvalue relationships for

From this the exponential is

We see that the eigenstates of are those of , with eigenvalues .

By the definition of the determinant given we have

1e. Eigenvectors of the Harmonic oscillator creation operator.

\paragraph{Q:} Prove that the only eigenvector of the Harmonic oscillator creation operator is .

\paragraph{A:}

Recall that the creation (raising) operator was given by

where . Now assume that so that

Write , and expand the LHS using 3.27 for

As usual write , and rearrange. This gives us

Observe that this can be viewed as a homogeneous LDE of the form

augmented by a forcing term . The homogeneous equation has the solution , so for the complete equation we assume a solution

Since , we produce a LDE of

or

This has solution , so our solution for 3.29 is

This wave function is an imaginary Gaussian with minimum at . It is also unnormalizable since we require for any if . Since , we must also have , completing the exercise.

2. Two level quantum system.

Consider a two-level quantum system, with basis states . Suppose that the Hamiltonian for this system is given by

where and are real positive constants.

\paragraph{Q: (a)} Find the energy eigenvalues and the normalized energy eigenvectors (expressed in terms of the basis). Write the time evolution operator using these eigenvectors.

\paragraph{A:}

The eigenvalue part of this problem is probably easier to do in matrix form. Let

Our Hamiltonian is then

Computing , we get

Let . Our normalized eigenvectors are found to be

In terms of and , we then have

Note that our Hamiltonian has a simple form in this basis. That is

Observe that once we do the diagonalization, we have a Hamiltonian that appears to have the form of a scaled projector for an open Stern-Gerlach aparatus.

Observe that the diagonalized Hamiltonian operator makes the time evolution operator’s form also simple, which is, by inspection

Since we are asked for this in terms of , and , the projectors are required. These are

Substitution into 3.42 and a fair amount of algebra leads to

Note that while a big cumbersome, we can also verify that we can recover the original Hamiltonian from 3.41 and 3.43.

\paragraph{Q: (b)}

Suppose that the initial state of the system at time is . Find an expression for the state at some later time , .

\paragraph{A:}

Most of the work is already done. Computation of follows from 3.44

\paragraph{Q: (c)}

Suppose that an observable, specified by the operator , is measured for this system. What is the probabilbity that, at time , the result is obtained? Plot this probability as a function of time, showing the maximum and minimum values of the function, and the corresponding values of .

\paragraph{A:}

The language of questions like these attempt to bring some physics into the mathematics. The phrase “the result is obtained”, is really a statement that the operator , after measurement is found to have the eigenstate with numeric value 1.

We can calcuate the eigenvectors for this operator easily enough and find them to be . For the positive eigenvalue we can also compute the eigenstate to be

The question of what the probability for this measurement is then really a question asking for the computation of the amplitude

From 3.45 we find this probability to be

We have a simple superposition of two sinusuiods out of phase, periodic with period . I’d attempted a rough sketch of this on paper, but won’t bother scanning it here or describing it further.

\paragraph{Q: (d)}

Suppose an experimenter has control over the values of the parameters and . Explain how she might prepare the state .

\paragraph{A:}

For this part of the question I wasn’t sure what approach to take. I thought perhaps this linear combination of states could be made to equal one of the energy eigenstates, and if one could prepare the system in that state, then for certain values of and one would then have this desired state.

To get there I note that we can express the states , and in terms of the eigenstates by inverting

Skipping all the algebra one finds

Unfortunately, this doesn’t seem helpful. I find

There’s no obvious way to pick and to leave just or . When I did this on paper originally I got a different answer for this sum, but looking at it now, I can’t see how I managed to get that answer (it had no factors of in the result as the one above does).

3. One dimensional harmonic oscillator.

Consider a one-dimensional harmonic oscillator with the Hamiltonian

Denote the ground state of the system by , the first excited state by and so on.

\paragraph{Q: (a)}
Evaluate and for arbitrary .

\paragraph{A:}

Writing in terms of the raising and lowering operators we have

so is proportional to

For we have

We are left with just

\paragraph{Q: (b)}

Suppose that at the system is prepared in the state

If a measurement of position were performaed immediately, sketch the propability distribution that a particle would be found within of . Justify how you construct the sketch.

\paragraph{A:}

The probability that we started in state and ended up in position is governed by the amplitude , and the probability of being within an interval , surrounding the point is given by

In the limit as , this is just the squared amplitude itself evaluated at the point , so we are interested in the quantity

We are given these wave functions in the supplemental formulas. Namely,

Substituting these into 3.57 we have

This \href{http://www.wolframalpha.com/input/?i=graph+e^(-x^2)+(1+

\paragraph{Q: (c)}

Now suppose the state given in (b) above were allowed to evolve for a time , determine the expecation value of and at that time.

\paragraph{A:}

Our time evolved state is

The position expectation is therefore

We have already demonstrated that , so we must only expand the cross terms, but those are just . This leaves

For the squared position expectation

Noting that , and , so we see the last two terms are zero. The first two we can evaluate using our previous result 3.54 which was . This leaves

Since , we have

\paragraph{Q: (d)}

Now suppose that initially the system were prepared in the ground state , and then the resonance frequency is changed abrubtly from to so that the Hamiltonian becomes

Immediately, an energy measurement is performed ; what is the probability of obtaining the result ?

\paragraph{A:}

This energy measurement , corresponds to an observation of state , after an initial observation of . The probability of such a measurement is

Note that

The wave functions above are

Putting the pieces together we have

Since this is an odd integral kernel over an even range, this evaluates to zero, and we conclude that the probability of measuring the specified energy is zero when the system is initially prepared in the ground state associated with the original Hamiltonian. Intuitively this makes some sense, if one thinks of the Fourier coefficient problem: one cannot construct an even function from linear combinations of purely odd functions.

Notes and problems for Desai Chapter V.

[Click here for a PDF of this post with nicer formatting]

Motivation.

Chapter V notes for [1].

Notes

Problems

Problem 1.

Statement.

Obtain for spin 1 in the representation in which and are diagonal.

Solution.

For spin 1, we have

and are interested in the states . If, like angular momentum, we assume that we have for

and introduce a column matrix representations for the kets as follows

then we have, by inspection

Note that, like the Pauli matrices, and unlike angular momentum, the spin states have not been considered. Do those have any physical interpretation?

That question aside, we can proceed as in the text, utilizing the ladder operator commutators

to determine the values of and indirectly. We find

Let

Looking for equality between , we find

so we must have

Furthermore, from , we find

We must have . We could probably pick any
, and , but assuming we have no reason for a non-zero phase we try

Putting all the pieces back together, with , and , we finally have

A quick calculation verifies that we have , as expected.

Problem 2.

Statement.

Obtain eigensolution for operator . Call the eigenstates and , and determine the probabilities that they will correspond to .

Solution.

The first part is straight forward, and we have

Taking we get

with eigenvectors proportional to

The normalization constant is . Now we can call these , and but what does the last part of the question mean? What’s meant by ?

Asking the prof about this, he says:

“I think it means that the result of a measurement of the x component of spin is . This corresponds to the eigenvalue of being . The spin operator has eigenvalue ”.

Aside: Question to consider later. Is is significant that ?

So, how do we translate this into a mathematical statement?

First let’s recall a couple of details. Recall that the x spin operator has the matrix representation

This has eigenvalues , with eigenstates . At the point when the x component spin is observed to be , the state of the system was then

Let’s look at the ways that this state can be formed as linear combinations of our states , and . That is

or

Letting , this is

We can solve the and with Cramer’s rule, yielding

or

It is and that are probabilities, and after a bit of algebra we find that those are

so if the x spin of the system is measured as , we have a $50\

Is that what the question was asking? I think that I’ve actually got it backwards. I think that the question was asking for the probability of finding state (measuring a spin 1 value for ) given the state or .

So, suppose that we have

or (considering both cases simultaneously),

or

Unsurprisingly, this mirrors the previous scenario and we find that we have a probability of measuring a spin 1 value for when the state of the operator has been measured as (ie: in the states , or respectively).

No measurement of the operator gives a biased prediction of the state of the state . Loosely, this seems to justify calling these operators orthogonal. This is consistent with the geometrical antisymmetric nature of the spin components where we have , just like two orthogonal vectors under the Clifford product.

Problem 3.

Statement.

Obtain the expectation values of for the case of a spin particle with the spin pointed in the direction of a vector with azimuthal angle and polar angle .

Solution.

Let’s work with instead of to eliminate the factors. Before considering the expectation values in the arbitrary spin orientation, let’s consider just the expectation values for . Introducing a matrix representation (assumed normalized) for a reference state

we find

Each of these expectation values are real as expected due to the Hermitian nature of . We also find that

So a vector formed with the expectation values as components is a unit vector. This doesn’t seem too unexpected from the section on the projection operators in the text where it was stated that , where was a unit vector, and this seems similar. Let’s now consider the arbitrarily oriented spin vector , and look at its expectation value.

With as the the rotated image of by an azimuthal angle , and polar angle , we have

that is

The projections of this operator

are just the Pauli matrices scaled by the components of

so our expectation values are by inspection

Is this correct? While is a unit norm operator, we find that the expectation values of the coordinates of cannot be viewed as the coordinates of a unit vector. Let’s consider a specific case, with , where the spin is oriented in the plane. That gives us

so the expectation values of are

Given this is seems reasonable that from 3.43 we find

(since we don’t have any reason to believe that in general is true).

The most general statement we can make about these expectation values (an average observed value for the measurement of the operator) is that

with equality for specific states and orientations only.

Problem 4.

Statement.

Take the azimuthal angle, , so that the spin is in the
x-z plane at an angle with respect to the z-axis, and the unit vector is . Write

for this case. Show that the probability that it is in the spin-up state in the direction with respect to the z-axis is

Also obtain the expectation value of with respect to the state .

Solution.

For this orientation we have

Confirmation that our eigenvalues are is simple, and our eigenstates for the eigenvalue is found to be

This last has unit norm, so we can write

If the state has been measured to be

then the probability of a second measurement obtaining is

Expanding just the inner product first we have

So our probability of measuring spin up state given the state was known to have been in spin up state is

Finally, the expectation value for with respect to is

Sanity checking this we observe that we have as desired for the case.

Problem 5.

Statement.

Consider an arbitrary density matrix, , for a spin system. Express each matrix element in terms of the ensemble averages where .

Solution.

Let’s omit the spin direction temporarily and write for the density matrix

For the ensemble average (no sum over repeated indexes) we have

This gives us

and our density matrix becomes

Utilizing

We can easily find

So we can write the density matrix in terms of any of the ensemble averages as

Alternatively, defining , for any of the directions we can write

In equation (5.109) we had a similar result in terms of the polarization vector , and the individual weights , and , but we see here that this factor can be written exclusively in terms of the ensemble average. Actually, this is also a result in the text, down in (5.113), but we see it here in a more concrete form having picked specific spin directions.

Problem 6.

Statement.

If a Hamiltonian is given by where , determine the time evolution operator as a 2 x 2 matrix. If a state at is given by

then obtain .

Solution.

Before diving into the meat of the problem, observe that a tidy factorization of the Hamiltonian is possible as a composition of rotations. That is

So we have for the time evolution operator

Does this really help? I guess not, but it is nice and tidy.

Returning to the specifics of the problem, we note that squaring the Hamiltonian produces the identity matrix

This allows us to exponentiate by inspection utilizing

Writing , and , we have

and thus

Note that as a sanity check we can calculate that as expected.

Now for , we have

It doesn’t seem terribly illuminating to multiply this all out, but we can factor the results slightly to tidy it up. That gives us

Problem 7.

Statement.

Consider a system of spin particles in a mixed ensemble containing a mixture of 25\

Solution.

We have

Giving us

Note that we can also factor the identity out of this for

which is just:

Recall that the ensemble average is related to the trace of the density and operator product

But this, by definition of the ensemble average, is just

We can use this to compute the ensemble averages of the Pauli matrices

We can also find without the explicit matrix multiplication from 3.70

(where to do so we observe that for and , and .)

We see that the traces of the density operator and Pauli matrix products act very much like dot products extracting out the ensemble averages, which end up very much like the magnitudes of the projections in each of the directions.

Problem 8.

Statement.

Show that the quantity , when simplified, has a term proportional to .

Solution.

Consider the operation

With , we have

which gives us the commutator

Insertion into the operator in question we have

With decomposition of the into symmetric and antisymmetric components, we should have in the second term our

where we expect . Alternately in components

Problem 9.

Statement.

Solution.

TODO.

References

[1] BR Desai. Quantum mechanics with basic field theory. Cambridge University Press, 2009.