May 2024
M	T	W	T	F	S	S
	1	2	3	4	5
6	7	8	9	10	11	12
13	14	15	16	17	18	19
20	21	22	23	24	25	26
27	28	29	30	31

Posts Tagged ‘statistical mechanics’

Final version of my phy452.pdf notes posted

Posted by peeterjoot on September 5, 2013

I’d intended to rework the exam problems over the summer and make that the last update to my stat mech notes. However, I ended up studying world events and some other non-mainstream ideas intensively over the summer, and never got around to that final update.

Since I’m starting a new course (condensed matter) soon, I’ll end up having to focus on that, and have now posted a final version of my notes as is.

Since the last update the following additions were made

September 05, 2013 Large volume fermi gas density

May 30, 2013 Bernoulli polynomials and numbers and Euler-MacLauren summation

May 09, 2013 Bose gas specific heat above condensation temperature

May 09, 2013 A dumb expansion of the Fermi-Dirac grand partition function

April 30, 2013 Ultra relativistic spin zero condensation temperature

April 30, 2013 Summary of statistical mechanics relations and helpful formulas

April 24, 2013 Low temperature Fermi gas chemical potential

Posted in Math and Physics Learning. | Tagged: average, Bernoulli number, Bernoulli polynomial, binomial distribution, Bose condensate, Bose gas, Bosons, canonical ensemble, Central limit theorem, cheat sheet, chemical potential, classical limit, density of states, ergodic, Euler-MacLauren summation, Fermi energy, Fermi gas, Fermi-Dirac, Fermions, fugacity, Generating function, grand canonical ensemble, grand canonical partition function, ground state, Hamilton's equations, Handy mathematics, ideal gas, large volume, Liouville's theorem, low temperature, Maxwell distribution, Microstates, number density, PHY452H1S, Quantum free particle in a box, Radius of gyration of a 3D polymer, random walk, specific heat, spin, statistical mechanics, statistics, Statistics mechanics, surface with binding sites, thermodynamics, ultra relativistic gas, Velocity, zeta function | Leave a Comment »

Large volume Fermi gas density

Posted by peeterjoot on September 5, 2013

[Click here for a PDF of this post with nicer formatting]

Here’s part of a problem from our final exam. I’d intended to redo the whole exam over the summer, but focused my summer study on world events instead. Perhaps I’ll end up eventually doing this, but for now I’ll just post this first part.

Question: Large volume Fermi gas density (2013 final exam pr 1)

Write down the expression for the grand canonical partition function $Z_{\mathrm{G}}$ of an ideal three-dimensional Fermi gas with atoms having mass $m$ at a temperature $T$ and a chemical potential $\mu$ (or equivalently a fugacity $z = e^{\beta \mu}$ ). Consider the high temperature “classical limit” of this ideal gas, where $z \ll 1$ and one gets an effective Boltzmann distribution, and obtain the equation for the density of the particles

$\begin{aligned}n = \frac{1}{{V \beta}} \frac{\partial {\ln Z_{\mathrm{G}}}}{\partial {\mu}}\end{aligned} \hspace{\stretch{1}}(1.1)$

by converting momentum sums into integrals. Invert this relationship to find the chemical potential $\mu$ as a function of the density $n$ .

Hint: In the limit of a large volume $V$ :

$\begin{aligned}\sum_\mathbf{k} \rightarrow V \int \frac{d^3 \mathbf{k}}{(2 \pi)^3}.\end{aligned} \hspace{\stretch{1}}(1.2)$

Answer

Since it was specified incorrectly in the original problem, let’s start off by verifing the expression for the number of particles (and hence the number density)

$\begin{aligned}\frac{1}{{\beta}} \frac{\partial {}}{\partial {\mu}} \ln Z_{\mathrm{G}} &= \frac{1}{{\beta}} \frac{\partial {}}{\partial {\mu}} \ln \sum_N z^N e^{-\beta E_N} \\ &= \frac{1}{{\beta}} \frac{1}{{\Omega}}\frac{\partial {}}{\partial {\mu}} \sum_N z^N e^{-\beta E_N} \\ &= \frac{1}{{\beta}} \frac{1}{{\Omega}}\sum_N e^{-\beta E_N} \frac{\partial {}}{\partial {\mu}} e^{\mu \beta N} \\ &= \frac{1}{{\Omega}}\sum_N N z^N e^{-\beta E_N} \\ &= \left\langle{{N}}\right\rangle.\end{aligned} \hspace{\stretch{1}}(1.3)$

Moving on to the problem, we’ve seen that the Fermion grand canonical partition function can be written

$\begin{aligned}Z_{\mathrm{G}} = \prod_\epsilon \left( { 1 + z e^{-\beta \epsilon}} \right),\end{aligned} \hspace{\stretch{1}}(1.4)$

so that our density is

$\begin{aligned}n &= \frac{N}{V} \\ &= \frac{1}{{ V \beta }}\frac{\partial {}}{\partial {\mu}} \ln \prod_\epsilon \left( { 1 + z e^{-\beta \epsilon}} \right) \\ &= \frac{1}{{ V \beta }}\sum_\epsilon \frac{\partial {}}{\partial {\mu}} \ln \left( { 1 + z e^{-\beta \epsilon}} \right) \\ &= \frac{1}{{ V \beta }}\sum_\epsilon \frac{\partial {z}}{\partial {\mu}}\frac{e^{-\beta \epsilon}}{1 + z e^{-\beta \epsilon}} \\ &= \frac{1}{{ V }}\sum_\epsilon z\frac{e^{-\beta \epsilon}}{1 + z e^{-\beta \epsilon}}.\end{aligned} \hspace{\stretch{1}}(1.5)$

In the high temperature classical limit, where $z \ll 1$ we have

$\begin{aligned}n \\ &\approx \frac{1}{ V } \sum_\epsilon z e^{-\beta \epsilon} \\ &\approx z \int \frac{d^3 \mathbf{k}}{(2 \pi)^3}e^{-\beta \epsilon} \\ &= \frac{2 z}{(2 \pi)^2} \int_0^\infty k^2 dk e^{-\beta \frac{\hbar^2 k^2}{2m} } \\ &= \frac{z}{2 \pi^2} \left( { \frac{\beta \hbar^2}{2m} } \right)^{-3/2} \int_0^\infty x^2 e^{-x^2} dx \\ &= \frac{z}{2 \pi^2} \left( { \frac{2m}{\beta \hbar^2} } \right)^{3/2} \frac{\sqrt{\pi}}{4} \\ &= \frac{z}{8 \pi^{3/2}} \frac{\left( {8 \pi^2 m k_{\mathrm{B}} T } \right)^{3/2}}{h^3} \\ &= z \frac{\left( { 2 \pi m k_{\mathrm{B}} T } \right)^{3/2}}{h^3}.\end{aligned} \hspace{\stretch{1}}(1.6)$

This is

$\begin{aligned}\boxed{n = \frac{z}{\lambda^3},}\end{aligned} \hspace{\stretch{1}}(1.7)$

where

$\begin{aligned}\lambda = \frac{h}{\sqrt{2 \pi m k_{\mathrm{B}} T}}.\end{aligned} \hspace{\stretch{1}}(1.8)$

Inverting for $\mu$ we have

$\begin{aligned}\mu = \frac{1}{\beta} \ln z\end{aligned} \hspace{\stretch{1}}(1.10)$

$\begin{aligned}\boxed{\mu = k_{\mathrm{B}} T \ln \left( { n \lambda^3 } \right).}\end{aligned} \hspace{\stretch{1}}(1.10)$

Posted in Math and Physics Learning. | Tagged: chemical potential, classical limit, Fermi gas, large volume, number density, PHY452H1S, statistical mechanics, surface with binding sites | Leave a Comment »

A dumb expansion of the Fermi-Dirac grand partition function

Posted by peeterjoot on May 9, 2013

[Click here for a PDF of this post with nicer formatting (especially if my latex to wordpress script has left FORMULA DOES NOT PARSE errors.)]

In section 6.2 [1] we have the following notation for the sums in the grand partition function $\Omega$ . Note that I’ve switched notations from $Z_G$ as used in class to $\Omega$ as used on our final exam. The text uses a script Q like $\mathcal{Q}$ but with the loop much more disconnected and hard to interpret.

$\begin{aligned}\Omega = \sum_{N = 0}^\infty z^N Q_N(V, T)\end{aligned} \hspace{\stretch{1}}(1.0.1a)$

$\begin{aligned}Q_N(V, T) = {\sum_{\{n_\epsilon\}}}' e^{-\beta \sum_\epsilon n_\epsilon \epsilon}.\end{aligned} \hspace{\stretch{1}}(1.0.1b)$

This was shorthand notation for the canonical ensemble, subject to constraints on $N$ and $E$

$\begin{aligned}Q_N(V, T) = \sum_E e^{-\beta E}\end{aligned} \hspace{\stretch{1}}(1.0.2a)$

$\begin{aligned}E = \sum_\epsilon n_\epsilon \epsilon\end{aligned} \hspace{\stretch{1}}(1.0.2b)$

$\begin{aligned}N = \sum_\epsilon n_\epsilon.\end{aligned} \hspace{\stretch{1}}(1.0.2c)$

I found this notation pretty confusing, since the normal conventions about what is a dummy index in the various summations do not hold.

The claim of the text (and in class) is that we could write out the grand canonical partition function as

$\begin{aligned}\Omega = \left(\sum_{n_0}\left( z e^{-\beta \epsilon_0} \right)^{n_0} \right)\left(\sum_{n_1}\left( z e^{-\beta \epsilon_1} \right)^{n_1} \right)\cdots\end{aligned} \hspace{\stretch{1}}(1.0.5)$

Let’s verify this for a Fermi-Dirac distribution by dispensing with the notational tricks and writing out the original specification of the grand canonical partition function in long form, and compare that to the first few terms of the expansion of eq. 1.0.5.

Let’s consider a specific value of $E$ , namely all those values of $E$ that apply to $N = 3$ . Note that we have $n_\epsilon \in \{0, 1\}$ only for a Fermi-Dirac sysstem, so this means we can have values of $E$ like

$\begin{aligned}E \in \{ \epsilon_0 + \epsilon_1 + \epsilon_2, \epsilon_0 + \epsilon_3 + \epsilon_7, \epsilon_2 + \epsilon_6 + \epsilon_{11}, \cdots\}\end{aligned} \hspace{\stretch{1}}(1.0.4)$

Our grand canonical partition function, when written out explicitly, will have the form

$\begin{aligned}\Omega = z^0 e^{-0}+ z^1 \sum_{\epsilon_k} e^{-\beta \epsilon_k}+ z^2 \sum_{\epsilon_k, \epsilon_m} e^{-\beta (\epsilon_k + \epsilon_m) }+ z^3 \sum_{\epsilon_r, \epsilon_s, \epsilon_t} e^{-\beta (\epsilon_r + \epsilon_s + \epsilon_t) }+ \cdots\end{aligned} \hspace{\stretch{1}}(1.0.5)$

Okay, that’s simple enough and really what the primed notation is getting at. Now let’s verify that after simplification this matches up with eq. 1.0.5. Expanding this out a bit we have

$\begin{aligned}\Omega &= \left(\sum_{n_0 = 0}^1\left( z e^{-\beta \epsilon_0} \right)^{n_0} \right)\left(\sum_{n_1 = 0}^1\left( z e^{-\beta \epsilon_1} \right)^{n_1} \right)\cdots \\ &= \left(1 + z e^{-\beta \epsilon_0} \right)\left(1 + z e^{-\beta \epsilon_1} \right)\left(1 + z e^{-\beta \epsilon_2} \right)\cdots \\ &= \left(1 + z e^{-\beta \epsilon_0} +z e^{-\beta \epsilon_1} +z e^{-\beta (\epsilon_0 + \epsilon_1)} \right)\left(1 + z e^{-\beta \epsilon_2} +z e^{-\beta \epsilon_3} +z^2 e^{-\beta (\epsilon_2 + \epsilon_3)} \right)\left(1 + z e^{-\beta \epsilon_4} \right)\cdots \\ &= \Bigl(1 + z \left(e^{-\beta \epsilon_0} +e^{-\beta \epsilon_1} +e^{-\beta \epsilon_2} +e^{-\beta \epsilon_3} \right) \\ &+\qquad z^2 \left(e^{-\beta (\epsilon_0 + \epsilon_1)} +e^{-\beta (\epsilon_0 + \epsilon_2)} +e^{-\beta (\epsilon_0 + \epsilon_3)} +e^{-\beta (\epsilon_1 + \epsilon_2)} +e^{-\beta (\epsilon_1 + \epsilon_3)} +e^{-\beta (\epsilon_2 + \epsilon_3)} \right) \\ &+ \qquad z^3\left(e^{-\beta (\epsilon_0 + \epsilon_1 + \epsilon_2)} + e^{-\beta (\epsilon_0 + \epsilon_1 + \epsilon_3)} + e^{-\beta (\epsilon_0 + \epsilon_2 + \epsilon_3)} + e^{-\beta (\epsilon_1 + \epsilon_2 + \epsilon_3)} \right)\Bigr)\left(1 + z e^{-\beta \epsilon_4} \right)\cdots\end{aligned} \hspace{\stretch{1}}(1.0.5)$

This completes the verification of the result as expected. It is definitely a brute force way of doing so, but easy to understand and I found for myself that it removed some of the notation that obfuscated what is really a simple statement.

Once we are comfortable with this Fermi-Dirac expression of the grand canonical partition function, we can then write it in the product form that leads to the sum that we want after taking logs

$\begin{aligned}\Omega &= \left(1 + z e^{-\beta \epsilon_0} \right)\left(1 + z e^{-\beta \epsilon_1} \right)\left(1 + z e^{-\beta \epsilon_2} \right)\cdots \\ &=\prod_\epsilon\left(1 + z e^{-\beta \epsilon} \right).\end{aligned} \hspace{\stretch{1}}(1.0.7)$

References

[1] RK Pathria. Statistical mechanics. Butterworth Heinemann, Oxford, UK, 1996.

Posted in Math and Physics Learning. | Tagged: Fermi-Dirac statistics, grand canonical partition function, PHY452H1S, statistical mechanics | Leave a Comment »

Ultra relativisitic spin zero condensation temperature

Posted by peeterjoot on April 30, 2013

[Click here for a PDF of this post with nicer formatting (especially if my latex to wordpress script has left FORMULA DOES NOT PARSE errors.)]

Here’s a bash at one of the exam questions, where I get the time to think things through properly. I think I did something like this on the exam itself, but may have also made some arithmetic errors.

Question: Ultra relativisitic spin zero condensation temperature (2013 final exam pr 2)

Consider a Bose gas with particles having no spin and obeying an ultra relativisitic dispersion $E_\mathbf{k} = c \left\lvert {\mathbf{k}} \right\rvert$ . Unlike photons or phonons, these particles are {\bf conserved}, and hence we must determine the chemical potential $\mu$ which fixes their density. Working in three dimensions, show whether or not these particles will exhibit Bose condensation, and find $T_c$ if it is nonzero.

Answer

For the number of particles in the gas, as with photons, we still have

$\begin{aligned}\left\langle{{N}}\right\rangle = \sum_\mathbf{k} \frac{1}{{z^{-1} e^{\beta \epsilon_\mathbf{k}} - 1}}= \frac{1}{{z^{-1} - 1}}+ \sum_{\mathbf{k} \ne 0} \frac{1}{{z^{-1} e^{\beta \epsilon_\mathbf{k}} - 1}}.\end{aligned} \hspace{\stretch{1}}(1.1)$

As in the discussion of low velocity particles in [1] section 7.1, the ground state term has been split out, before making any continuum approximation of the sum over the energetic states.

Writing

$\begin{aligned}\left\langle{{N}}\right\rangle = N_0 + N_e,\end{aligned} \hspace{\stretch{1}}(1.0.2)$

where the number of particles in the ground state is chemical potential and temperature dependent

$\begin{aligned}N_0 = \frac{z}{1 - z}.\end{aligned} \hspace{\stretch{1}}(1.0.3)$

We proceed with the continuum approximation for the number of particles in the energetic states

$\begin{aligned}N_e &= \sum_{\mathbf{k} \ne 0} \frac{1}{{z^{-1} e^{\beta \epsilon_\mathbf{k}} - 1}} \\ &\sim V \int \frac{d^3 \mathbf{k}}{(2 \pi)^3}\frac{1}{{z^{-1} e^{\beta \epsilon_\mathbf{k}} - 1}} \\ &= \frac{4 \pi V}{(2 \pi)^3} \int_0^\infty k^2 dk\frac{1}{{z^{-1} e^{\beta c k} - 1}} \\ &= \frac{V}{2 \pi^2} \left( { \frac{1}{{\beta c}} } \right)^3\int_0^\infty x^2 dx\frac{1}{{z^{-1} e^{x} - 1}} \\ &= \frac{V}{2 \pi^2} \left( { \frac{1}{{\beta c}} } \right)^3\Gamma(3) g_3(z).\end{aligned} \hspace{\stretch{1}}(1.0.3)$

So we have

$\begin{aligned}N_e=\frac{V}{\pi^2} \left( { \frac{k_{\mathrm{B}} T}{c} } \right)^3g_3(z)\le \frac{V}{\pi^2} \left( { \frac{k_{\mathrm{B}} T}{c} } \right)^3\zeta(3).\end{aligned} \hspace{\stretch{1}}(1.0.5)$

Note that $\zeta(3) \approx 1.20206$ , a fixed number. The key feature of Bose condensation remains. There is a finite limit to the number of particles that can be in the energetic state at a given temperature and volume. Any remaining particles are forced into the ground state.

In general the number of particles in the ground state is

$\begin{aligned}N_0 = N - \frac{V}{\pi^2} \left( { \frac{k_{\mathrm{B}} T}{c} } \right)^3g_3(z),\end{aligned} \hspace{\stretch{1}}(1.0.6)$

and we will necessarily have particles in this state if

$\begin{aligned}N - \frac{V}{\pi^2} \left( { \frac{k_{\mathrm{B}} T}{c} } \right)^3\zeta(3) > 0.\end{aligned} \hspace{\stretch{1}}(1.0.7)$

That temperature threshold $T \le T_c$ is the Bose condensation temperature

$\begin{aligned}\boxed{k_{\mathrm{B}} T_c = c \left( { \frac{n \pi^2}{\zeta(3)} } \right)^{1/3}.}\end{aligned} \hspace{\stretch{1}}(1.0.8)$

With $n = N/V$ , $n_0 = N_0/V$ , we have for the ground state average number density

$\begin{aligned}n_0 = n\left( 1 - \frac{g_3(z)}{\zeta(3)} \left( { \frac{T}{T_c} } \right)^3 \right)\end{aligned} \hspace{\stretch{1}}(1.0.9)$

This is plotted in fig. 1.1.

Fig 1.1: Ratio of ground state number density to total number density

From the figure it appears that the notion of any sort of absolute condensation temperature is an approximation. We can start having particles go into the ground state at higher temperatures than $T_c$ , but once the chemical potential starts approaching zero, that temperature for which we start having particles in the ground state approaches $T_c$ . The key takeout idea appears to be, once the temperature does drop below $T_c$ , we necessarily start having a non-zero ground state population, and as the temperature drops more and more, the ratio of the number of particles in the ground state relative to the total approaches unity (all particles are forced into the ground state).

References

[1] RK Pathria. Statistical mechanics. Butterworth Heinemann, Oxford, UK, 1996.

Posted in Math and Physics Learning. | Tagged: average number density, Bose condensate, ground state number density, PHY452H1S, statistical mechanics, ultra relativisitic gas, zeta function | Leave a Comment »

Summary of statistical mechanics relations and helpful formulas (cheat sheet fodder)

Posted by peeterjoot on April 29, 2013

[Click here for a PDF of this post with nicer formatting (especially if my latex to wordpress script has left FORMULA DOES NOT PARSE errors.)]

Central limit theorem

If $\left\langle{{x}}\right\rangle = \mu$ and $\sigma^2 = \left\langle{{x^2}}\right\rangle - \left\langle{{x}}\right\rangle^2$ , and $X = \sum x$ , then in the limit

$\begin{aligned}\lim_{N \rightarrow \infty} P(X)= \frac{1}{{\sigma \sqrt{2 \pi N}}} \exp\left( - \frac{ (x - N \mu)^2}{2 N \sigma^2} \right)\end{aligned} \hspace{\stretch{1}}(1.0.1a)$

$\begin{aligned}\left\langle{{X}}\right\rangle = N \mu\end{aligned} \hspace{\stretch{1}}(1.0.1b)$

$\begin{aligned}\left\langle{{X^2}}\right\rangle - \left\langle{{X}}\right\rangle^2 = N \sigma^2\end{aligned} \hspace{\stretch{1}}(1.0.1c)$

Binomial distribution

$\begin{aligned}P_N(X) = \left\{\begin{array}{l l}\left(\frac{1}{{2}}\right)^N \frac{N!}{\left(\frac{N-X}{2}\right)!\left(\frac{N+X}{2}\right)!}& \quad \mbox{if X and N have same parity} \\ 0 & \quad \mbox{otherwise} \end{array},\right.\end{aligned} \hspace{\stretch{1}}(1.0.2)$

where $X$ was something like number of Heads minus number of Tails.

Generating function

Given the Fourier transform of a probability distribution $\tilde{P}(k)$ we have

$\begin{aligned}{\left.{{ \frac{\partial^n}{\partial k^n} \tilde{P}(k) }}\right\vert}_{{k = 0}}= (-i)^n \left\langle{{x^n}}\right\rangle\end{aligned} \hspace{\stretch{1}}(1.0.2)$

Handy mathematics

$\begin{aligned}\ln( 1 + x ) = x - \frac{x^2}{2} + \frac{x^3}{3} - \frac{x^4}{4}\end{aligned} \hspace{\stretch{1}}(1.0.2)$

$\begin{aligned}N! \approx \sqrt{ 2 \pi N} N^N e^{-N}\end{aligned} \hspace{\stretch{1}}(1.0.5)$

$\begin{aligned}\ln N! \approx \frac{1}{{2}} \ln 2 \pi -N + \left( N + \frac{1}{{2}} \right)\ln N \approx N \ln N - N\end{aligned} \hspace{\stretch{1}}(1.0.6)$

$\begin{aligned}\text{erf}(z) = \frac{2}{\sqrt{\pi}} \int_0^z e^{-t^2} dt\end{aligned} \hspace{\stretch{1}}(1.0.7)$

$\begin{aligned}\Gamma(\alpha) = \int_0^\infty dy e^{-y} y^{\alpha - 1}\end{aligned} \hspace{\stretch{1}}(1.0.8)$

$\begin{aligned}\Gamma(\alpha + 1) = \alpha \Gamma(\alpha)\end{aligned} \hspace{\stretch{1}}(1.0.9)$

$\begin{aligned}\Gamma\left( 1/2 \right) = \sqrt{\pi}\end{aligned} \hspace{\stretch{1}}(1.0.10)$

$\begin{aligned}\zeta(s) = \sum_{k=1}^{\infty} k^{-s}\end{aligned} \hspace{\stretch{1}}(1.0.10)$

$\begin{aligned}\begin{aligned}\zeta(3/2) &\approx 2.61238 \\ \zeta(2) &\approx 1.64493 \\ \zeta(5/2) &\approx 1.34149 \\ \zeta(3) &\approx 1.20206\end{aligned}\end{aligned} \hspace{\stretch{1}}(1.0.12)$

$\begin{aligned}\Gamma(z) \Gamma(1-z) = \frac{\pi}{\sin(\pi z)}\end{aligned} \hspace{\stretch{1}}(1.0.12)$

$\begin{aligned}P(x, t) = \int_{-\infty}^\infty \frac{dk}{2 \pi} \tilde{P}(k, t) \exp\left( i k x \right)\end{aligned} \hspace{\stretch{1}}(1.0.14a)$

$\begin{aligned}\tilde{P}(k, t) = \int_{-\infty}^\infty dx P(x, t) \exp\left( -i k x \right)\end{aligned} \hspace{\stretch{1}}(1.0.14b)$

Heavyside theta

$\begin{aligned}\Theta(x) = \left\{\begin{array}{l l}1 & \quad x \ge 0 \\ 0 & \quad x < 0\end{array}\right.\end{aligned} \hspace{\stretch{1}}(1.0.15a)$

$\begin{aligned}\frac{d\Theta}{dx} = \delta(x)\end{aligned} \hspace{\stretch{1}}(1.0.15b)$

$\begin{aligned}\sum_{m = -l}^l a^m=\frac{a^{l + 1/2} - a^{-(l+1/2)}}{a^{1/2} - a^{-1/2}}\end{aligned} \hspace{\stretch{1}}(1.0.16.16)$

$\begin{aligned}\sum_{m = -l}^l e^{b m}=\frac{\sinh(b(l + 1/2))}{\sinh(b/2)}\end{aligned} \hspace{\stretch{1}}(1.0.16b)$

$\begin{aligned}\int_{-\infty}^\infty q^{2 N} e^{-a q^2} dq=\frac{(2 N - 1)!!}{(2a)^N} \sqrt{\frac{\pi}{a}}\end{aligned} \hspace{\stretch{1}}(1.0.17.17)$

$\begin{aligned}\int_{-\infty}^\infty e^{-a q^2} dq=\sqrt{\frac{\pi}{a}}\end{aligned} \hspace{\stretch{1}}(1.0.17.17)$

$\begin{aligned}\binom{-\left\lvert {m} \right\rvert}{k} = (-1)^k \frac{\left\lvert {m} \right\rvert}{\left\lvert {m} \right\rvert + k} \binom{\left\lvert {m} \right\rvert+k}{\left\lvert {m} \right\rvert}\end{aligned} \hspace{\stretch{1}}(1.0.18)$

$\begin{aligned}\int_0^\infty d\epsilon \frac{\epsilon^3}{e^{\beta \epsilon} - 1} =\frac{\pi ^4}{15 \beta ^4},\end{aligned} \hspace{\stretch{1}}(1.0.18)$

volume in mD

$\begin{aligned}V_m= \frac{ \pi^{m/2} R^{m} }{ \Gamma\left( m/2 + 1 \right)}\end{aligned} \hspace{\stretch{1}}(1.0.20)$

area of ellipse

$\begin{aligned}A = \pi a b\end{aligned} \hspace{\stretch{1}}(1.0.21)$

Radius of gyration of a 3D polymer

With radius $a$ , we have

$\begin{aligned}r_N \approx a \sqrt{N}\end{aligned} \hspace{\stretch{1}}(1.0.21)$

Velocity random walk

Find

$\begin{aligned}\mathcal{P}_{N_{\mathrm{c}}}(\mathbf{v}) \propto e^{-\frac{(\mathbf{v} - \mathbf{v}_0)^2}{2 N_{\mathrm{c}}}}\end{aligned} \hspace{\stretch{1}}(1.0.23)$

Random walk

1D Random walk

$\begin{aligned}\mathcal{P}( x, t ) = \frac{1}{{2}} \mathcal{P}(x + \delta x, t - \delta t)+\frac{1}{{2}} \mathcal{P}(x - \delta x, t - \delta t)\end{aligned} \hspace{\stretch{1}}(1.0.23)$

leads to

$\begin{aligned}\frac{\partial {\mathcal{P}}}{\partial {t}}(x, t) =\frac{1}{{2}} \frac{(\delta x)^2}{\delta t}\frac{\partial^2 {{\mathcal{P}}}}{\partial {{x}}^2}(x, t) = D \frac{\partial^2 {{\mathcal{P}}}}{\partial {{x}}^2}(x, t) = -\frac{\partial {J}}{\partial {x}},\end{aligned} \hspace{\stretch{1}}(1.0.25)$

The diffusion constant relation to the probability current is referred to as Fick’s law

$\begin{aligned}D = -\frac{\partial {J}}{\partial {x}}\end{aligned} \hspace{\stretch{1}}(1.0.25)$

with which we can cast the probability diffusion identity into a continuity equation form

$\begin{aligned}\frac{\partial {\mathcal{P}}}{\partial {t}} + \frac{\partial {J}}{\partial {x}} = 0 \end{aligned} \hspace{\stretch{1}}(1.0.25)$

In 3D (with the Maxwell distribution frictional term), this takes the form

$\begin{aligned}\mathbf{j} = -D \boldsymbol{\nabla}_\mathbf{v} c(\mathbf{v}, t) - \eta \mathbf{v} c(\mathbf{v}, t)\end{aligned} \hspace{\stretch{1}}(1.0.28a)$

$\begin{aligned}\frac{\partial {}}{\partial {t}} c(\mathbf{v}, t) + \boldsymbol{\nabla}_\mathbf{v} \cdot \mathbf{j}(\mathbf{v}, t) = 0\end{aligned} \hspace{\stretch{1}}(1.0.28b)$

Maxwell distribution

Add a frictional term to the velocity space diffusion current

$\begin{aligned}j_v = -D \frac{\partial {c}}{\partial {v}}(v, t) - \eta v c(v).\end{aligned} \hspace{\stretch{1}}(1.0.29)$

For steady state the continity equation $0 = \frac{dc}{dt} = -\frac{\partial {j_v}}{\partial {v}}$ leads to

$\begin{aligned}c(v) \propto \exp\left(- \frac{\eta v^2}{2 D}\right).\end{aligned} \hspace{\stretch{1}}(1.0.30)$

We also find

$\begin{aligned}\left\langle{{v^2}}\right\rangle = \frac{D}{\eta},\end{aligned} \hspace{\stretch{1}}(1.0.30)$

and identify

$\begin{aligned}\frac{1}{{2}} m \left\langle{{\mathbf{v}^2}}\right\rangle = \frac{1}{{2}} m \left( \frac{D}{\eta} \right) = \frac{1}{{2}} k_{\mathrm{B}} T\end{aligned} \hspace{\stretch{1}}(1.0.32)$

Hamilton’s equations

$\begin{aligned}\frac{\partial {H}}{\partial {p}} = \dot{x}\end{aligned} \hspace{\stretch{1}}(1.0.33a)$

$\begin{aligned}\frac{\partial {H}}{\partial {x}} = -\dot{p}\end{aligned} \hspace{\stretch{1}}(1.0.33b)$

SHO

$\begin{aligned}H = \frac{p^2}{2m} + \frac{1}{{2}} k x^2\end{aligned} \hspace{\stretch{1}}(1.0.34a)$

$\begin{aligned}\omega^2 = \frac{k}{m}\end{aligned} \hspace{\stretch{1}}(1.0.34b)$

Quantum energy eigenvalues

$\begin{aligned}E_n = \left( n + \frac{1}{{2}} \right) \hbar \omega\end{aligned} \hspace{\stretch{1}}(1.0.35)$

Liouville’s theorem

$\begin{aligned}\frac{d{{\rho}}}{dt} = \frac{\partial {\rho}}{\partial {t}} + \dot{x} \frac{\partial {\rho}}{\partial {x}} + \dot{p} \frac{\partial {\rho}}{\partial {p}}= \cdots = \frac{\partial {\rho}}{\partial {t}} + \frac{\partial {\left( \dot{x} \rho \right)}}{\partial {x}} + \frac{\partial {\left( \dot{x} \rho \right)}}{\partial {p}} = \frac{\partial {\rho}}{\partial {t}} + \boldsymbol{\nabla}_{x,p} \cdot (\rho \dot{x}, \rho \dot{p})= \frac{\partial {\rho}}{\partial {t}} + \boldsymbol{\nabla} \cdot \mathbf{J}= 0,\end{aligned} \hspace{\stretch{1}}(1.0.35)$

Regardless of whether we have a steady state system, if we sit on a region of phase space volume, the probability density in that neighbourhood will be constant.

Ergodic

A system for which all accessible phase space is swept out by the trajectories. This and Liouville’s threorm allows us to assume that we can treat any given small phase space volume as if it is equally probable to the same time evolved phase space region, and switch to ensemble averaging instead of time averaging.

Thermodynamics

$\begin{aligned}dE = T dS - P dV + \mu dN\end{aligned} \hspace{\stretch{1}}(1.0.37.37)$

$\begin{aligned}\frac{1}{{T}} = \left({\partial {S}}/{\partial {E}}\right)_{{N,V}}\end{aligned} \hspace{\stretch{1}}(1.0.37.37)$

$\begin{aligned}\frac{P}{T} = \left({\partial {S}}/{\partial {V}}\right)_{{N,E}}\end{aligned} \hspace{\stretch{1}}(1.0.37.37)$

$\begin{aligned}-\frac{\mu}{T} = \left({\partial {S}}/{\partial {N}}\right)_{{V,E}}\end{aligned} \hspace{\stretch{1}}(1.0.37.37)$

$\begin{aligned}P = - \left({\partial {E}}/{\partial {V}}\right)_{{N,S}}= - \left({\partial {F}}/{\partial {V}}\right)_{{N,T}}\end{aligned} \hspace{\stretch{1}}(1.0.37e)$

$\begin{aligned}\mu = \left({\partial {E}}/{\partial {N}}\right)_{{V,S}} = \left({\partial {F}}/{\partial {N}}\right)_{{V,T}}\end{aligned} \hspace{\stretch{1}}(1.0.37e)$

$\begin{aligned}T = \left({\partial {E}}/{\partial {S}}\right)_{{N,V}}\end{aligned} \hspace{\stretch{1}}(1.0.37e)$

$\begin{aligned}F = E - TS\end{aligned} \hspace{\stretch{1}}(1.0.37e)$

$\begin{aligned}G = F + P V = E - T S + P V = \mu N\end{aligned} \hspace{\stretch{1}}(1.0.37i)$

$\begin{aligned}H = E + P V = G + T S\end{aligned} \hspace{\stretch{1}}(1.0.37j)$

$\begin{aligned}C_{\mathrm{V}} = T \left({\partial {S}}/{\partial {T}}\right)_{{N,V}} = \left({\partial {E}}/{\partial {T}}\right)_{{N,V}} = - T \left( \frac{\partial^2 {{F}}}{\partial {{T}}^2} \right)_{N,V}\end{aligned} \hspace{\stretch{1}}(1.0.37k)$

$\begin{aligned}C_{\mathrm{P}} = T \left({\partial {S}}/{\partial {T}}\right)_{{N,P}} = \left({\partial {H}}/{\partial {T}}\right)_{{N,P}}\end{aligned} \hspace{\stretch{1}}(1.0.37l)$

$\begin{aligned}\underbrace{dE}_{\text{Change in energy}}=\underbrace{d W}_{\text{work done on the system}}+\underbrace{d Q}_{\text{Heat supplied to the system}}\end{aligned} \hspace{\stretch{1}}(1.0.38)$

Example (work on gas): $d W = -P dV$ . Adiabatic: $d Q = 0$ . Cyclic: $dE = 0$ .

Microstates

$\begin{aligned}\beta = \frac{1}{k_{\mathrm{B}} T}\end{aligned} \hspace{\stretch{1}}(1.0.38)$

$\begin{aligned}S = k_{\mathrm{B}} \ln \Omega \end{aligned} \hspace{\stretch{1}}(1.0.40)$

$\begin{aligned}\Omega(N, V, E) = \frac{1}{h^{3N} N!} \int_V d\mathbf{x}_1 \cdots d\mathbf{x}_N \int d\mathbf{p}_1 \cdots d\mathbf{p}_N \delta \left(E - \frac{\mathbf{p}_1^2}{2 m} \cdots - \frac{\mathbf{p}_N^2}{2 m}\right)=\frac{V^N}{h^{3N} N!}\int d\mathbf{p}_1 \cdots d\mathbf{p}_N \delta \left(E - \frac{\mathbf{p}_1^2}{2m} \cdots - \frac{\mathbf{p}_N^2}{2m}\right)\end{aligned} \hspace{\stretch{1}}(1.0.40)$

$\begin{aligned}\Omega = \frac{d\gamma}{dE}\end{aligned} \hspace{\stretch{1}}(1.0.42)$

$\begin{aligned}\gamma=\frac{V^N}{h^{3N} N!}\int d\mathbf{p}_1 \cdots d\mathbf{p}_N \Theta \left(E - \frac{\mathbf{p}_1^2}{2m} \cdots - \frac{\mathbf{p}_N^2}{2m}\right)\end{aligned} \hspace{\stretch{1}}(1.0.43)$

quantum

$\begin{aligned}\gamma = \sum_i \Theta(E - \epsilon_i)\end{aligned} \hspace{\stretch{1}}(1.0.44)$

Ideal gas

$\begin{aligned}\Omega = \frac{V^N}{N!} \frac{1}{{h^{3N}}} \frac{( 2 \pi m E)^{3 N/2 }}{E} \frac{1}{\Gamma( 3N/2 ) }\end{aligned} \hspace{\stretch{1}}(1.0.45)$

$\begin{aligned}S_{\mathrm{ideal}} = k_{\mathrm{B}} \left(N \ln \frac{V}{N} + \frac{3 N}{2} \ln \left( \frac{4 \pi m E }{3 N h^2} \right) + \frac{5 N}{2} \right)\end{aligned} \hspace{\stretch{1}}(1.0.46)$

Quantum free particle in a box

$\begin{aligned}\Psi_{n_1, n_2, n_3}(x, y, z) = \left( \frac{2}{L} \right)^{3/2} \sin\left( \frac{ n_1 \pi x}{L} \right)\sin\left( \frac{ n_2 \pi x}{L} \right)\sin\left( \frac{ n_3 \pi x}{L} \right)\end{aligned} \hspace{\stretch{1}}(1.0.47a)$

$\begin{aligned}\epsilon_{n_1, n_2, n_3} = \frac{h^2}{8 m L^2} \left( n_1^2 + n_2^2 + n_3^2 \right)\end{aligned} \hspace{\stretch{1}}(1.0.47b)$

$\begin{aligned}\epsilon_k = \frac{\hbar^2 k^2}{2m},\end{aligned} \hspace{\stretch{1}}(1.0.47b)$

Spin

magnetization

$\begin{aligned}\mu = \frac{\partial {F}}{\partial {B}}\end{aligned} \hspace{\stretch{1}}(1.0.48)$

moment per particle

$\begin{aligned}m = \mu/N\end{aligned} \hspace{\stretch{1}}(1.0.49)$

spin matrices

$\begin{aligned}\sigma_x = \begin{bmatrix} 0 & 1 \\ 1 & 0 \\ \end{bmatrix}\end{aligned} \hspace{\stretch{1}}(1.0.50a)$

$\begin{aligned}\sigma_y = \begin{bmatrix} 0 & -i \\ i & 0 \\ \end{bmatrix}\end{aligned} \hspace{\stretch{1}}(1.0.50b)$

$\begin{aligned}\sigma_z = \begin{bmatrix} 1 & 0 \\ 0 & -1 \\ \end{bmatrix}\end{aligned} \hspace{\stretch{1}}(1.0.50c)$

$l \ge 0, -l \le m \le l$

$\begin{aligned}\mathbf{L}^2 {\left\lvert {lm} \right\rangle} = l(l+1)\hbar^2 {\left\lvert {lm} \right\rangle}\end{aligned} \hspace{\stretch{1}}(1.0.51a)$

$\begin{aligned}L_z {\left\lvert {l m} \right\rangle} = \hbar m {\left\lvert {l m} \right\rangle}\end{aligned} \hspace{\stretch{1}}(1.0.51b)$

spin addition

$\begin{aligned}S(S + 1) \hbar^2\end{aligned} \hspace{\stretch{1}}(1.0.51b)$

Canonical ensemble

classical

$\begin{aligned}\Omega(N, E) = \frac{ V }{ h^3 N} \int d\mathbf{p}_1 e^{\frac{S}{k_{\mathrm{B}}}(N, E)}e^{-\frac{1}{{k_{\mathrm{B}}}} \left( \frac{\partial {S}}{\partial {N}} \right)_{E, V} }e^{-\frac{\mathbf{p}_1^2}{2m k_{\mathrm{B}}}\left( \frac{\partial {S}}{\partial {E}} \right)_{N, V}}\end{aligned} \hspace{\stretch{1}}(1.0.53)$

quantum

$\begin{aligned}\Omega(E) \approx\sum_{m \in \text{subsystem}} e^{\frac{1}{{k_{\mathrm{B}}}} S(E)}e^{-\beta \mathcal{E}_m}\end{aligned} \hspace{\stretch{1}}(1.0.54.54)$

$\begin{aligned}Z = \sum_m e^{-\beta \mathcal{E}_m} = \text{Tr} \left( e^{-\beta \hat{H}_{\text{subsystem}}} \right)\end{aligned} \hspace{\stretch{1}}(1.0.54b)$

$\begin{aligned}\left\langle{{E}}\right\rangle = \frac{\int He^{- \beta H }}{\int e^{- \beta H }}\end{aligned} \hspace{\stretch{1}}(1.0.55a)$

$\begin{aligned}\left\langle{{E^2}}\right\rangle = \frac{\int H^2e^{- \beta H }}{\int e^{- \beta H }}\end{aligned} \hspace{\stretch{1}}(1.0.55b)$

$\begin{aligned}Z \equiv \frac{1}{{h^{3N} N!}}\int e^{- \beta H }\end{aligned} \hspace{\stretch{1}}(1.0.55c)$

$\begin{aligned}\left\langle{{E}}\right\rangle = -\frac{1}{{Z}} \frac{\partial {Z}}{\partial {\beta}} = - \frac{\partial {\ln Z}}{\partial {\beta}} =\frac{\partial {(\beta F)}}{\partial {\beta}}\end{aligned} \hspace{\stretch{1}}(1.0.55d)$

$\begin{aligned}\sigma_{\mathrm{E}}^2= \left\langle{{E^2}}\right\rangle - \left\langle{{E}}\right\rangle^2 =\frac{\partial^2 {{\ln Z}}}{\partial {{\beta}}^2} = k_{\mathrm{B}} T^2 \frac{\partial {\left\langle{{E}}\right\rangle}}{\partial {T}}= k_{\mathrm{B}} T^2 C_{\mathrm{V}} \propto N\end{aligned} \hspace{\stretch{1}}(1.0.55e)$

$\begin{aligned}Z = e^{-\beta (\left\langle{{E}}\right\rangle - T S) } = e^{-\beta F}\end{aligned} \hspace{\stretch{1}}(1.0.55f)$

$\begin{aligned}F = \left\langle{{E}}\right\rangle - T S = -k_{\mathrm{B}} T \ln Z\end{aligned} \hspace{\stretch{1}}(1.0.55g)$

Grand Canonical ensemble

$\begin{aligned}S = - k_{\mathrm{B}} \sum_{r,s} P_{r,s} \ln P_{r,s}\end{aligned} \hspace{\stretch{1}}(1.0.56)$

$\begin{aligned}P_{r, s} = \frac{e^{-\alpha N_r - \beta E_s}}{Z_{\mathrm{G}}}\end{aligned} \hspace{\stretch{1}}(1.0.57a)$

$\begin{aligned}Z_{\mathrm{G}} = \sum_{r,s} e^{-\alpha N_r - \beta E_s} = \sum_{r,s} z^{N_r} e^{-\beta E_s} = \sum_{N_r} z^{N_r} Z_{N_r}\end{aligned} \hspace{\stretch{1}}(1.0.57b)$

$\begin{aligned}z = e^{-\alpha} = e^{\mu \beta}\end{aligned} \hspace{\stretch{1}}(1.0.57c)$

$\begin{aligned}q = \ln Z_{\mathrm{G}} = P V \beta\end{aligned} \hspace{\stretch{1}}(1.0.57d)$

$\begin{aligned}\left\langle{{H}}\right\rangle = -\left({\partial {q}}/{\partial {\beta}}\right)_{{z,V}} = k_{\mathrm{B}} T^2 \left({\partial {q}}/{\partial {\mu}}\right)_{{z,V}} = \sum_\epsilon \frac{\epsilon}{z^{-1} e^{\beta \epsilon} \pm 1}\end{aligned} \hspace{\stretch{1}}(1.0.57e)$

$\begin{aligned}\left\langle{{N}}\right\rangle = z \left({\partial {q}}/{\partial {z}}\right)_{{V,T}} = \sum_\epsilon \frac{1}{{z^{-1} e^{\beta\epsilon} \pm 1}}\end{aligned} \hspace{\stretch{1}}(1.0.57f)$

$\begin{aligned}F = - k_{\mathrm{B}} T \ln \frac{ Z_{\mathrm{G}} }{z^N}\end{aligned} \hspace{\stretch{1}}(1.0.57g)$

$\begin{aligned}\left\langle{{n_\epsilon}}\right\rangle = -\frac{1}{{\beta}} \left({\partial {q}}/{\partial {\epsilon}}\right)_{{z, T, \text{other} \epsilon}} = \frac{1}{{z^{-1} e^{\beta \epsilon} \pm 1}}\end{aligned} \hspace{\stretch{1}}(1.0.57h)$

$\begin{aligned}\text{var}(N) = \frac{1}{{\beta}} \left({\partial {\left\langle{{N}}\right\rangle}}/{\partial {\mu}}\right)_{{V, T}} = - \frac{1}{{\beta}} \left({\partial {\left\langle{{n_\epsilon}}\right\rangle}}/{\partial {\epsilon}}\right)_{{z,T}} = z^{-1} e^{\beta \epsilon}\end{aligned} \hspace{\stretch{1}}(1.0.57h)$

$\begin{aligned}\mathcal{P} \propto e^{\frac{\mu}{k_{\mathrm{B}} T} N_S}e^{-\frac{E_S}{k_{\mathrm{B}} T} }\end{aligned} \hspace{\stretch{1}}(1.0.59.59)$

$\begin{aligned}Z_{\mathrm{G}}= \sum_{N=0}^\infty e^{\beta \mu N}\sum_{n_k, \sum n_m = N} e^{-\beta \sum_m n_m \epsilon_m}=\prod_{k} \left( \sum_{n_k} e^{-\beta(\epsilon_k - \mu) n_k} \right)\end{aligned} \hspace{\stretch{1}}(1.0.59b)$

$\begin{aligned}Z_{\mathrm{G}}^{\mathrm{QM}} = {\text{Tr}}_{\{\text{energy}, N\}} \left( e^{ -\beta (\hat{H} - \mu \hat{N} ) } \right)\end{aligned} \hspace{\stretch{1}}(1.0.59b)$

$\begin{aligned}P V = \frac{2}{3} U\end{aligned} \hspace{\stretch{1}}(1.0.60a)$

$\begin{aligned}f_\nu^\pm(z) = \frac{1}{{\Gamma(\nu)}} \int_0^\infty dx \frac{x^{\nu - 1}}{z^{-1} e^x \pm 1}\end{aligned} \hspace{\stretch{1}}(1.0.60a)$

$\begin{aligned}f_\nu^\pm(z \approx 0) =z\mp\frac{z^{2}}{2^\nu}+\frac{z^{3}}{3^\nu}\mp\frac{z^{4}}{4^\nu}+ \cdots \end{aligned} \hspace{\stretch{1}}(1.0.60a)$

$\begin{aligned}z \frac{d f_\nu^{\pm}(z) }{dz} = f_{\nu-1}^{\pm}(z)\end{aligned} \hspace{\stretch{1}}(1.0.61)$

$\begin{aligned}\frac{d f_{3/2}^{\pm}(z) }{dT} = -\frac{3}{2T} f_{3/2}^{\pm}(z)f_{\nu-1}^{\pm}(z)\end{aligned} \hspace{\stretch{1}}(1.0.62)$

Fermions

$\begin{aligned}\sum_{n_k = 0}^1 e^{-\beta(\epsilon_k - \mu) n_k}=1 + e^{-\beta(\epsilon_k - \mu)}\end{aligned} \hspace{\stretch{1}}(1.0.62)$

$\begin{aligned}N = (2 S + 1) V \int_0^{k_{\mathrm{F}}} \frac{4 \pi k^2 dk}{(2 \pi)^3}\end{aligned} \hspace{\stretch{1}}(1.0.64)$

$\begin{aligned}k_{\mathrm{F}} = \left( \frac{ 6 \pi^2 \rho }{2 S + 1} \right)^{1/3}\end{aligned} \hspace{\stretch{1}}(1.0.65.65)$

$\begin{aligned}\epsilon_{\mathrm{F}} = \frac{\hbar^2}{2m} \left( \frac{6 \pi \rho}{2 S + 1} \right)^{2/3}\end{aligned} \hspace{\stretch{1}}(1.0.65.65)$

$\begin{aligned}\mu = \epsilon_{\mathrm{F}} - \frac{\pi^2}{12} \frac{(k_{\mathrm{B}} T)^2}{\epsilon_{\mathrm{F}}} + \cdots \end{aligned} \hspace{\stretch{1}}(1.0.65.65)$

$\begin{aligned}\lambda \equiv \frac{h}{\sqrt{2 \pi m k_{\mathrm{B}} T}}\end{aligned} \hspace{\stretch{1}}(1.0.65.65)$

$\begin{aligned}\frac{N}{V}=\frac{g}{\lambda^3} f_{3/2}(z)=\frac{g}{\lambda^3} \left( e^{\beta \mu} - \frac{e^{2 \beta \mu}}{2^{3/2}} + \cdots \right) \end{aligned} \hspace{\stretch{1}}(1.0.68)$

(so $n = \frac{g}{\lambda^3} e^{\beta \mu}$ for large temperatures)

$\begin{aligned}P \beta = \frac{g}{\lambda^3} f_{5/2}(z)\end{aligned} \hspace{\stretch{1}}(1.0.69a)$

$\begin{aligned}U= \frac{3}{2} N k_{\mathrm{B}} T \frac{f_{5/2}(z)}{f_{3/2}(z) }.\end{aligned} \hspace{\stretch{1}}(1.0.69a)$

$\begin{aligned}f_\nu^+(e^y) \approx\frac{y^\nu}{\Gamma(\nu + 1)}\left( 1 + 2 \nu \sum_{j = 1, 3, 5, \cdots } (\nu-1) \cdots (\nu - j) \left( 1 - 2^{-j} \right) \frac{\zeta(j+1)}{ y^{j + 1} } \right)\end{aligned} \hspace{\stretch{1}}(1.0.69a)$

$\begin{aligned}\frac{C}{N} = \frac{\pi^2}{2} k_{\mathrm{B}} \frac{ k_{\mathrm{B}} T}{\epsilon_{\mathrm{F}}}\end{aligned} \hspace{\stretch{1}}(1.0.71.71)$

$\begin{aligned}A = N k_{\mathrm{B}} T \left( \ln z - \frac{f_{5/2}(z)}{f_{3/2}(z)} \right)\end{aligned} \hspace{\stretch{1}}(1.0.71.71)$

Bosons

$\begin{aligned}Z_{\mathrm{G}} = \prod_\epsilon \frac{1}{{ 1 - z e^{-\beta \epsilon} }}\end{aligned} \hspace{\stretch{1}}(1.0.72)$

$\begin{aligned}P \beta = \frac{1}{{\lambda^3}} g_{5/2}(z)\end{aligned} \hspace{\stretch{1}}(1.0.73)$

$\begin{aligned}U = \frac{3}{2} k_{\mathrm{B}} T \frac{V}{\lambda^3} g_{5/2}(z)\end{aligned} \hspace{\stretch{1}}(1.0.74)$

$\begin{aligned}N_e = N - N_0 = N \left( \frac{T}{T_c} \right)^{3/2}\end{aligned} \hspace{\stretch{1}}(1.0.75)$

For $T < T_c$ , $z = 1$ .

$\begin{aligned}g_\nu(1) = \zeta(\nu).\end{aligned} \hspace{\stretch{1}}(1.0.76)$

$\begin{aligned}\sum_{n_k = 0}^\infty e^{-\beta(\epsilon_k - \mu) n_k} =\frac{1}{{1 - e^{-\beta(\epsilon_k - \mu)}}}\end{aligned} \hspace{\stretch{1}}(1.0.76)$

$\begin{aligned}f_\nu^-( e^{-\alpha} ) = \frac{ \Gamma(1 - \nu)}{ \alpha^{1 - \nu} } + \cdots \end{aligned} \hspace{\stretch{1}}(1.0.76)$

$\begin{aligned}\rho \lambda^3 = g_{3/2}(z) \le \zeta(3/2) \approx 2.612\end{aligned} \hspace{\stretch{1}}(1.0.79.79)$

$\begin{aligned}k_{\mathrm{B}} T_{\mathrm{c}} = \left( \frac{\rho}{\zeta(3/2)} \right)^{2/3} \frac{ 2 \pi \hbar^2}{m}\end{aligned} \hspace{\stretch{1}}(1.0.79.79)$

BEC

$\begin{aligned}\rho= \rho_{\mathbf{k} = 0}+ \frac{1}{{\lambda^3}} g_{3/2}(z)\end{aligned} \hspace{\stretch{1}}(1.0.80.80)$

$\begin{aligned}\rho_0 = \rho \left(1 - \left( \frac{T}{T_{\mathrm{c}}} \right)^{3/2}\right)\end{aligned} \hspace{\stretch{1}}(1.0.80b)$

$\begin{aligned}\frac{E}{V} \propto \left( k_{\mathrm{B}} T \right)^{5/2}\end{aligned} \hspace{\stretch{1}}(1.0.81.81)$

$\begin{aligned}\frac{C}{V} \propto \left( k_{\mathrm{B}} T \right)^{3/2}\end{aligned} \hspace{\stretch{1}}(1.0.81.81)$

$\begin{aligned}\frac{S}{N k_{\mathrm{B}}} = \frac{5}{2} \frac{g_{5/2}}{g_{3/2}} - \ln z \Theta(T - T_c)\end{aligned} \hspace{\stretch{1}}(1.0.81.81)$

Density of states

Low velocities

$\begin{aligned}N_1(\epsilon)=V \frac{m \hbar}{\hbar^2 \sqrt{ 2 m \epsilon}}\end{aligned} \hspace{\stretch{1}}(1.0.82a)$

$\begin{aligned}N_2(\epsilon)=V \frac{m}{\hbar^2}\end{aligned} \hspace{\stretch{1}}(1.0.82b)$

$\begin{aligned}N_3(\epsilon)=V \left( \frac{2 m}{\hbar^2} \right)^{3/2} \frac{1}{{4 \pi^2}} \sqrt{\epsilon}\end{aligned} \hspace{\stretch{1}}(1.0.82c)$

relativistic

$\begin{aligned}\mathcal{D}_1(\epsilon)=\frac{2 L}{ c h } \frac{ \sqrt{ \epsilon^2 - \left( m c^2 \right)^2} }{\epsilon}\end{aligned} \hspace{\stretch{1}}(1.0.83.83)$

$\begin{aligned}\mathcal{D}_2(\epsilon)=\frac{2 \pi A}{ (c h)^2 } \frac{ \epsilon^2 - \left( m c^2 \right)^2 }{ \epsilon }\end{aligned} \hspace{\stretch{1}}(1.0.83.83)$

$\begin{aligned}\mathcal{D}_3(\epsilon)=\frac{4 \pi V}{ (c h)^3 } \frac{\left( \epsilon^2 - \left( m c^2 \right)^2 \right)^{3/2}}{\epsilon}\end{aligned} \hspace{\stretch{1}}(1.0.83.83)$

Posted in Math and Physics Learning. | Tagged: binomial distribution, Bosons, canonical ensemble, Central limit theorem, cheat sheet, density of states, ergodic, Fermions, Generating function, grand canonical ensemble, Hamilton's equations, Handy mathematics, ideal gas, Liouville's theorem, Maxwell distribution, Microstates, PHY452H1S, Quantum free particle in a box, Radius of gyration of a 3D polymer, random walk, spin, statistical mechanics, thermodynamics, Velocity random walk | Leave a Comment »

Low temperature Fermi gas chemical potential

Posted by peeterjoot on April 24, 2013

[Click here for a PDF of this post with nicer formatting (especially if my latex to wordpress script has left FORMULA DOES NOT PARSE errors.)]

Question: Low temperature Fermi gas chemical potential

[1] section 8.1 equation (33) provides an implicit function for $\mu \equiv k_{\mathrm{B}} T \ln z$

$\begin{aligned}n = \frac{4 \pi g}{3} \left( \frac{2m}{h^2} \right)^{3/2}\mu^{3/2}\left( 1 + \frac{\pi^2}{8} \frac{ (k_{\mathrm{B}} T)^2 }{ \mu^2 } + \cdots \right),\end{aligned} \hspace{\stretch{1}}(1.0.1)$

$\begin{aligned}E_{\mathrm{F}}^{3/2} = \mu^{3/2} \left( 1 + \frac{\pi^2}{8} \frac{ (k_{\mathrm{B}} T)^2 }{ \mu^2 } + \cdots \right).\end{aligned} \hspace{\stretch{1}}(1.0.2)$

In class, we assumed that $\mu$ was quadratic in $k_{\mathrm{B}} T$ as a mechanism to invert this non-linear equation. Without making this quadratic assumption find the lowest order, non-constant approximation for $\mu(T)$ .

Answer

To determine an approximate inversion, let’s start by multiplying eq. 1.0.2 by $\mu^{1/2}/E_{\mathrm{F}}^2$ to non-dimensionalize things

$\begin{aligned}\left( \frac{\mu}{E_{\mathrm{F}}} \right)^{1/2} = \left( \frac{\mu}{E_{\mathrm{F}}} \right)^2 + \frac{\pi^2}{8} \left( \frac{k_{\mathrm{B}} T}{E_{\mathrm{F}}} \right)^2,\end{aligned} \hspace{\stretch{1}}(1.0.3)$

$\begin{aligned}\left( \frac{\mu}{E_{\mathrm{F}}} \right)^{1/2} =\frac{1}{{ 1 - \left( \frac{\mu}{E_{\mathrm{F}}} \right)^{3/2} }}\frac{\pi^2}{8} \left( \frac{k_{\mathrm{B}} T}{E_{\mathrm{F}}} \right)^2.\end{aligned} \hspace{\stretch{1}}(1.0.4)$

If we are looking for an approximation in the neighborhood of $\mu = E_{\mathrm{F}}$ , then the LHS factor is approximately one, whereas the fractional difference term is large (with a corresponding requirement for $k_{\mathrm{B}} T/E_{\mathrm{F}}$ to be small. We must then have

$\begin{aligned}\left( \frac{\mu}{E_{\mathrm{F}}} \right)^{3/2} \approx 1 - \frac{\pi^2}{8} \left( \frac{k_{\mathrm{B}} T}{E_{\mathrm{F}}} \right)^2,\end{aligned} \hspace{\stretch{1}}(1.0.4)$

$\begin{aligned}\mu\approx E_{\mathrm{F}}\left(1 - \frac{\pi^2}{8} \left( \frac{k_{\mathrm{B}} T}{E_{\mathrm{F}}} \right)^2\right)^{2/3}\approx E_{\mathrm{F}}\left(1 - \frac{2}{3} \frac{\pi^2}{8} \left( \frac{k_{\mathrm{B}} T}{E_{\mathrm{F}}} \right)^2\right).\end{aligned} \hspace{\stretch{1}}(1.0.4)$

This gives us the desired result

$\begin{aligned}\boxed{\mu \approx E_{\mathrm{F}}\left(1 - \frac{\pi^2}{12} \left( \frac{k_{\mathrm{B}} T}{E_{\mathrm{F}}} \right)^2\right).}\end{aligned} \hspace{\stretch{1}}(1.0.7)$

References

[1] RK Pathria. Statistical mechanics. Butterworth Heinemann, Oxford, UK, 1996.

Posted in Math and Physics Learning. | Tagged: chemical potential, Fermi energy, Fermi gas, low temperature, PHY452H1S, statistical mechanics | Leave a Comment »

A final pre-exam update of my notes compilation for ‘PHY452H1S Basic Statistical Mechanics’, Taught by Prof. Arun Paramekanti

Posted by peeterjoot on April 22, 2013

Here’s my third update of my notes compilation for this course, including all of the following:

April 21, 2013 Fermi function expansion for thermodynamic quantities

April 20, 2013 Relativistic Fermi Gas

April 10, 2013 Non integral binomial coefficient

April 10, 2013 energy distribution around mean energy

April 09, 2013 Velocity volume element to momentum volume element

April 04, 2013 Phonon modes

April 03, 2013 BEC and phonons

April 03, 2013 Max entropy, fugacity, and Fermi gas

April 02, 2013 Bosons

April 02, 2013 Relativisitic density of states

March 28, 2013 Bosons

plus everything detailed in the description of my previous update and before.

Posted in Math and Physics Learning. | Tagged: average energy, average energy density, average number of particles, average occupancy, BEC temperature, binomial coefficient, binomial series, Boltzmann factor, Bose condensate, Bose condensation, Bose-Einstein condensate, Boson, canonical ensemble, chemical potential, configurations, constraint, delta function, density, density of states, distribution function, energy, energy density, ensemble, entropy, extreme relativistic gas, factorial, Fermi energy, Fermi gas, Fermi-Dirac function, Fermion, fugacity, Gamma function, Gibbs entropy, grand canonical ensemble, harmonic oscillator, Helium-4, jacobian, Lagrange multiplier, mean energy, microstate, momentum, momentum space volume element, neutrino gas, neutron star, nucleon, number density, occupation number, phonon, phonon modes, photon, photon gas, PHY452H1S, Polarization, pressure, probability, relativistic, relativistic gas, special relativity, specific heat, spherical coordinates, statistical mechanics, Taylor expansion, temperature, velocity space volume element, volume, zeta function | 1 Comment »

Relativisitic Fermi gas

Posted by peeterjoot on April 20, 2013

[Click here for a PDF of this post with nicer formatting (especially if my latex to wordpress script has left FORMULA DOES NOT PARSE errors.)]

Question: Relativisitic Fermi gas ([1], pr 9.3)

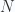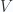Consider a relativisitic gas of $N$ particles of spin $1/2$ obeying Fermi statistics, enclosed in volume $V$ , at absolute zero. The energy-momentum relation is

$\begin{aligned}\epsilon = \sqrt{(p c)^2 + \epsilon_0^2},\end{aligned} \hspace{\stretch{1}}(1.1)$

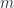where $\epsilon_0 = m c^2$ , and $m$ is the rest mass.

Find the Fermi energy at density $n$ .

With the pressure $P$ defined as the average force per unit area exerted on a perfectly-reflecting wall of the container.

Set up expressions for this in the form of an integral.

Define the internal energy $U$ as the average $\epsilon - \epsilon_0$ .
Set up expressions for this in the form of an integral.

Show that $P V = 2 U/3$ at low densities, and $P V = U/3$ at high densities. State the criteria for low and high densities.

There may exist a gas of neutrinos (and/or antineutrinos) in the cosmos. (Neutrinos are massless Fermions of spin $1/2$ .) Calculate the Fermi energy (in eV) of such a gas, assuming a density of one particle per $\text{cm}^3$ .

Attempt exact evaluation of the various integrals.

Answer

We’ve found [3] that the density of states associated with a 3D relativisitic system is

$\begin{aligned}\mathcal{D}(\epsilon) = \frac{4 \pi V}{(c h)^3} \epsilon \sqrt{\epsilon^2 -\epsilon_0^2},\end{aligned} \hspace{\stretch{1}}(1.0.2)$

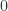For a given density $n$ , we can find the Fermi energy in the same way as we did for the non-relativisitic energies, with the exception that we have to integrate from a lowest energy of $\epsilon_0$ instead of $0$ (the energy at $\mathbf{p} = 0$ ). That is

$\begin{aligned}n &= \frac{N}{V} \\ &= \left( 2 \frac{1}{{2}} + 1 \right)\frac{4 \pi}{(c h)^3} \int_{\epsilon_0}^{\epsilon_{\mathrm{F}}}d\epsilon \epsilon \sqrt{ \epsilon^2 -\epsilon_0^2} \\ &= \frac{8 \pi}{(c h)^3}\frac{1}{{3}} {\left.{{\left( x^2 - \epsilon_0^2 \right)^{3/2}}}\right\vert}_{{\epsilon_0}}^{{\epsilon_{\mathrm{F}}}} \\ &= \frac{8 \pi}{3 (c h)^3}\left( \epsilon_{\mathrm{F}}^2 - \epsilon_0^2 \right)^{3/2}.\end{aligned} \hspace{\stretch{1}}(1.0.2)$

Solving for $\epsilon_{\mathrm{F}}/\epsilon_0$ we have

$\begin{aligned}\frac{\epsilon_{\mathrm{F}}}{\epsilon_0} =\sqrt{\left( \frac{3 (c h)^3 n}{8 \pi \epsilon_0^3} \right)^{2/3}+ 1}.\end{aligned} \hspace{\stretch{1}}(1.0.2)$

We’ll see the constant factor above a number of times below and designate it

$\begin{aligned}n_0 = \frac{8 \pi}{3} \left( \frac{\epsilon_0}{c h} \right)^3,\end{aligned} \hspace{\stretch{1}}(1.0.2)$

so that the Fermi energy is

$\begin{aligned}\frac{\epsilon_{\mathrm{F}}}{\epsilon_0} =\sqrt{\left( \frac{n}{n_0} \right)^{2/3}+ 1}.\end{aligned} \hspace{\stretch{1}}(1.0.2)$

For the pressure calculation, let’s suppose that we have a configuration with a plane in the 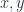$x,y$ orientation as in fig. 1.1.

Fig 1.1: Pressure against x,y oriented plane

It’s argued in [4] section 6.4 that the pressure for such a configuration is

$\begin{aligned}P = n \int p_z u_z f(\mathbf{u}) d^3 \mathbf{u},\end{aligned} \hspace{\stretch{1}}(1.7)$

where $n$ is the number density and $f(\mathbf{u})$ is a normalized distribution function for the velocities. The velocity and momentum components are related by the Hamiltonian equations. From the Hamiltonian eq. 1.1 we find \footnote{ Observe that by squaring and summing one can show that this is equivalent to the standard relativisitic momentum $p_x = \frac{m v_x}{\sqrt{ 1 - \mathbf{u}^2/c^2}}$ .} (for the x-component which is representative)

$\begin{aligned}u_x \\ &= \frac{\partial {\epsilon}}{\partial {p_x}} \\ &= \frac{\partial {}}{\partial {p_x}}\sqrt{(p c)^2 +\epsilon_0^2} \\ &= \frac{ p_x c^2 }{\sqrt{(p c)^2 +\epsilon_0^2}}.\end{aligned} \hspace{\stretch{1}}(1.8)$

For $\alpha \in \{1, 2, 3\}$ we can summarize these velocity-momentum relationships as

$\begin{aligned}\frac{u_\alpha}{c} = \frac{ c p_\alpha }{ \epsilon }.\end{aligned} \hspace{\stretch{1}}(1.9)$

Should we attempt to calculate the pressure with this parameterization of the velocity space we end up with convergence problems, and can’t express the results in terms of $f^+_\nu(z)$ . Let’s try instead with a distribution over momentum space

$\begin{aligned}P=n \int \frac{(c p_z)^2}{\epsilon} f(c \mathbf{p}) d^3 (c \mathbf{p}).\end{aligned} \hspace{\stretch{1}}(1.10)$

Here the momenta have been scaled to have units of energy since we want to express this integral in terms of energy in the end. Our normalized distribution function is

$\begin{aligned}f(c \mathbf{p})\propto \frac{\frac{1}{{ z^{-1} e^{\beta \epsilon} + 1 }}}{\int \frac{1}{{ z^{-1} e^{\beta \epsilon} + 1 }} d^3 (c \mathbf{p})},\end{aligned} \hspace{\stretch{1}}(1.11)$

but before evaluating anything, we first want to change our integration variable from momentum to energy. In spherical coordinates our volume element takes the form

$\begin{aligned}d^3 (c \mathbf{p}) &= 2 \pi (c p)^2 d (c p) \sin\theta d\theta \\ &= 2 \pi (c p)^2 \frac{d (c p)}{d \epsilon} d \epsilon \sin\theta d\theta.\end{aligned} \hspace{\stretch{1}}(1.12)$

Implicit derivatives of

$\begin{aligned}c^2 p^2 = \epsilon^2 - \epsilon_0^2,\end{aligned} \hspace{\stretch{1}}(1.13)$

gives us

$\begin{aligned}\frac{d (c p)}{d\epsilon}= \frac{\epsilon}{c p}=\frac{\epsilon}{\sqrt{\epsilon^2 -\epsilon_0^2}}.\end{aligned} \hspace{\stretch{1}}(1.0.14)$

Our momentum volume element becomes

$\begin{aligned}d^3 (c \mathbf{p}) \\ &= 2 \pi (c p)^2 \frac{\epsilon}{\sqrt{\epsilon^2 - \epsilon_0^2 }}d \epsilon \sin\theta d\theta \\ &= 2 \pi \left( \epsilon^2 - \epsilon_0^2 \right)\frac{\epsilon}{\sqrt{\epsilon^2 - \epsilon_0^2 }}d \epsilon \sin\theta d\theta \\ &= 2 \pi \epsilon \sqrt{ \epsilon^2 - \epsilon_0^2} d \epsilon \sin\theta d\theta.\end{aligned} \hspace{\stretch{1}}(1.0.14)$

For our distribution function, we can now write

$\begin{aligned}f(c \mathbf{p}) d^3 (c \mathbf{p})= C \frac{\epsilon \sqrt{ \epsilon^2 - \epsilon_0^2} d \epsilon }{ z^{-1} e^{\beta \epsilon} + 1 }\frac{ 2 \pi \sin\theta d\theta }{ 4 \pi \epsilon_0^3 },\end{aligned} \hspace{\stretch{1}}(1.0.14)$

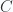where $C$ is determined by the requirement $\int f(c \mathbf{p}) d^3 (c \mathbf{p}) = 1$

$\begin{aligned}C^{-1} = \int_{0}^\infty \frac{(y + 1)\sqrt{ (y + 1)^2 - 1} dy }{ z^{-1} e^{\beta \epsilon_0 (y + 1)} + 1 }.\end{aligned} \hspace{\stretch{1}}(1.0.14)$

The z component of our momentum can be written in spherical coordinates as

$\begin{aligned}(c p_z)^2= (c p)^2 \cos^2\theta= \left( \epsilon^2 - \epsilon_0^2 \right)\cos^2\theta,\end{aligned} \hspace{\stretch{1}}(1.0.18)$

Noting that

$\begin{aligned}\int_0^\pi \cos^2\theta \sin\theta d\theta =-\int_0^\pi \cos^2\theta d(\cos\theta)= \frac{2}{3},\end{aligned} \hspace{\stretch{1}}(1.0.19)$

all the bits come together as

$\begin{aligned}P &= \frac{C n}{3 \epsilon_0^3 } \int_{\epsilon_0}^\infty\left( \epsilon^2 - \epsilon_0^2 \right)^{3/2} \frac{1}{{ z^{-1} e^{\beta \epsilon} + 1 }} d \epsilon \\ &= \frac{n \epsilon_0}{3} \int_{1}^\infty\left( x^2 - 1 \right)^{3/2} \frac{1}{{ z^{-1} e^{\beta \epsilon_0 x} + 1 }} dx.\end{aligned} \hspace{\stretch{1}}(1.0.19)$

Letting $y = x - 1$ , this is

$\begin{aligned}P= \frac{C n \epsilon_0}{3} \int_{0}^\infty \frac{ \left( (y + 1)^2 - 1 \right)^{3/2} } { z^{-1} e^{\beta \epsilon_0 (y + 1)} + 1 } dy.\end{aligned} \hspace{\stretch{1}}(1.0.19)$

We could conceivable expand the numerators of each of these integrals in power series, which could then be evaluated as a sum of $f^+_\nu(z e^{-\beta \epsilon_0})$ terms.

Note that above the Fermi energy $n$ also has an integral representation

$\begin{aligned}n &= \left(2\left( \frac{1}{{2}} \right) + 1\right)\int_{\epsilon_0}^\infty d\epsilon \mathcal{D}(\epsilon) \frac{1}{{ z^{-1} e^{\beta \epsilon} + 1}} \\ &= \frac{8 \pi}{(c h)^3} \int_{\epsilon_0}^\infty d\epsilon\frac{\epsilon \sqrt{\epsilon^2 - \epsilon_0^2} }{ z^{-1} e^{\beta \epsilon} + 1} \\ &= \frac{8 \pi \epsilon_0^3}{(c h)^3} \int_{0}^\infty dy\frac{(y + 1)\sqrt{(y + 1)^2 - 1} }{ z^{-1} e^{\beta \epsilon_0 (y + 1)} + 1},\end{aligned} \hspace{\stretch{1}}(1.0.19)$

$\begin{aligned}\boxed{n = \frac{3 n_0}{C}.}\end{aligned} \hspace{\stretch{1}}(1.0.23)$

Observe that we can use this result to remove the dependence of pressure on this constant 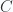$C$

$\begin{aligned}\boxed{\frac{P}{n_0 \epsilon_0}= \int_{0}^\infty dy \frac{ \left( (y + 1)^2 - 1 \right)^{3/2} } { z^{-1} e^{\beta \epsilon_0 (y + 1)} + 1 }.}\end{aligned} \hspace{\stretch{1}}(1.0.24)$

Now for the average energy difference from the rest energy $\epsilon_0$

$\begin{aligned}U &= \left\langle{{\epsilon - \epsilon_0}}\right\rangle \\ &= \int_{\epsilon_0}^\infty d\epsilon \mathcal{D}(\epsilon) f(\epsilon) (\epsilon - \epsilon_0) \\ &= \frac{8 \pi V}{(c h)^3}\int_{\epsilon_0}^\infty d\epsilon \frac{ \epsilon(\epsilon - \epsilon_0) \sqrt{ \epsilon^2 - \epsilon_0 } }{ z^{-1} e^{\beta \epsilon} + 1} \\ &= \frac{8 \pi V \epsilon_0^4}{(c h)^3}\int_{0}^\infty dy\frac{ y ( y - 1 ) \sqrt{ (y + 1)^2 - 1 }}{ z^{-1} e^{\beta \epsilon} + 1}.\end{aligned} \hspace{\stretch{1}}(1.0.24)$

So the average energy density difference from the rest energy, relative to the rest energy, is

$\begin{aligned}\boxed{\frac{\left\langle{{\epsilon - \epsilon_0}}\right\rangle}{V \epsilon_0} =3 n_0 \int_{0}^\infty dy \frac { y (y + 1)\sqrt{(y + 1)^2 - 1} } { z^{-1} e^{\beta \epsilon_0 (y + 1)} + 1 }.}\end{aligned} \hspace{\stretch{1}}(1.0.26)$

From eq. 1.0.24 and eq. 1.0.26 we have

$\begin{aligned}\frac{1}{{n_0}} &= 3 \frac{V \epsilon_0} {\left\langle{{\epsilon - \epsilon_0}}\right\rangle} \int_{0}^\infty \frac { y (y + 1)\sqrt{(y + 1)^2 - 1} dy } { z^{-1} e^{\beta \epsilon_0 (y + 1)} + 1 } \\ &= \frac{\epsilon_0}{P} \int_{0}^\infty \frac{ \left( (y + 1)^2 - 1 \right)^{3/2} } { z^{-1} e^{\beta \epsilon_0 (y + 1)} + 1 } dy,\end{aligned} \hspace{\stretch{1}}(1.0.26)$

$\begin{aligned}P V =\frac{U}{3}\frac{ \int_{0}^\infty \frac{ \left( (y + 1)^2 - 1 \right)^{3/2} } { z^{-1} e^{\beta \epsilon_0 (y + 1)} + 1 } dy}{ \int_{0}^\infty \frac { y (y + 1)\sqrt{(y + 1)^2 - 1} dy } { z^{-1} e^{\beta \epsilon_0 (y + 1)} + 1 }}.\end{aligned} \hspace{\stretch{1}}(1.0.26)$

This ratio of integrals is supposed to resolve to 1 and 2 in the low and high density limits. To consider this let’s perform one final non-dimensionalization, writing

$\begin{aligned}\begin{aligned} \\ x &= \beta \epsilon_0 y \\ \theta &= \frac{1}{{\beta \epsilon_0}} = \frac{k_{\mathrm{B}} T}{\epsilon_0} \\ \bar{\mu} &= \mu - \epsilon_0 \\ \bar{z} &= e^{\beta \bar{\mu}}.\end{aligned}\end{aligned} \hspace{\stretch{1}}(1.0.29)$

The density, pressure, and energy take the form

$\begin{aligned}\frac{n}{n_0}= 3 \theta\int_{0}^\infty dx\frac{(\theta x + 1)\sqrt{(\theta x + 1)^2 - 1} }{ \bar{z}^{-1} e^{x} + 1}\end{aligned} \hspace{\stretch{1}}(1.0.30a)$

$\begin{aligned}\frac{P}{n_0 \epsilon_0}= \theta \int_{0}^\infty dx \frac{ \left( (\theta x + 1)^2 - 1 \right)^{3/2} } { \bar{z}^{-1} e^{x} + 1 }\end{aligned} \hspace{\stretch{1}}(1.0.30b)$

$\begin{aligned}\frac{\left\langle{{\epsilon - \epsilon_0}}\right\rangle}{V \epsilon_0 n_0} =3 \theta^2 \int_{0}^\infty dx \frac { x (\theta x + 1)\sqrt{(\theta x + 1)^2 - 1} } { \bar{z}^{-1} e^{x} + 1 }.\end{aligned} \hspace{\stretch{1}}(1.0.30c)$

We can rewrite the square roots in the number density and energy density expressions by expanding out the completion of the square

$\begin{aligned}(1 + \theta x) \sqrt{ (1 + \theta x)^2 - 1}=(1 + \theta x) \sqrt{ 1 + \theta x + 1 }\sqrt{ 1 + \theta x - 1 }= \sqrt{2 \theta} x^{1/2} (1 + \theta x) \sqrt{ 1 + \frac{\theta x}{2}},\end{aligned} \hspace{\stretch{1}}(1.0.30c)$

Expanding the distribution about $\bar{z} e^{-x} = 0$ , we have

$\begin{aligned}\frac{1}{ \bar{z}^{-1} e^{x} + 1}=\frac{\bar{z} e^{-x}}{ 1 + \bar{z} e^{-x}}=z e^{-x} \sum_{s = 0}^\infty (-1)^s \left( \bar{z} e^{-x} \right)^s,\end{aligned} \hspace{\stretch{1}}(1.0.32)$

allowing us to write, in the low density limit with respect to $\bar{z}$

$\begin{aligned}\frac{n}{n_0}= 3 \sqrt{2}\theta^{3/2} \sum_{s=0}^\infty(-1)^s\bar{z}^{s + 1}\int_{0}^\infty dx x^{1/2}(1 + \theta x) \sqrt{ 1 + \frac{\theta x}{2}} e^{-x(1 + s)} \end{aligned} \hspace{\stretch{1}}(1.0.33a)$

$\begin{aligned}\frac{P}{n_0 \epsilon_0}= \theta\sum_{s=0}^\infty(-1)^s\bar{z}^{s + 1} \int_{0}^\infty dx\left( (\theta x + 1)^2 - 1 \right)^{3/2} e^{-x(1 + s)} \end{aligned} \hspace{\stretch{1}}(1.0.33b)$

$\begin{aligned}\frac{\left\langle{{\epsilon - \epsilon_0}}\right\rangle}{V \epsilon_0 n_0} =3 \sqrt{2} \theta^{5/2} \sum_{s=0}^\infty(-1)^s\bar{z}^{s + 1} \int_{0}^\infty dx x^{3/2} (1 + \theta x) \sqrt{ 1 + \frac{\theta x}{2}} e^{-x(1 + s)} .\end{aligned} \hspace{\stretch{1}}(1.0.33c)$

Low density result

An exact integration of the various integrals above is possible in terms of special functions. However, that attempt (included below) introduced an erroneous extra factor of 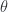$\theta$ . Given that this end result was obtained by tossing all but the lowest order terms in 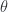$\theta$ and $\bar{z}$ , let’s try that right from the get go.

For the pressure we have an integrand containing a factor

$\begin{aligned}\left( (\theta x + 1)^2 -1 \right)^{3/2}&= \left( \theta x + 1 - 1 \right)^{3/2}\left( \theta x + 1 + 1 \right)^{3/2} \\ &= \theta^{3/2} x^{3/2} 2^{3/2} \left( 1 + \frac{\theta x}{2} \right)^{3/2} \\ &= 2 \sqrt{2} \theta^{3/2} x^{3/2} \left( 1 + \frac{\theta x}{2} \right)^{3/2}\approx2 \sqrt{2} \theta^{3/2} x^{3/2} \end{aligned} \hspace{\stretch{1}}(1.0.33c)$

Our pressure, to lowest order in 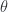$\theta$ and $\bar{z}$ is then

$\begin{aligned}\frac{P}{\epsilon_0 n_0} = 2 \sqrt{2} \theta^{5/2} \bar{z} \int_0^\infty x^{3/2} e^{-x} dx= 2 \sqrt{2} \theta^{5/2} \bar{z} \Gamma(5/2).\end{aligned} \hspace{\stretch{1}}(1.0.33c)$

Our energy density to lowest order in 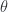$\theta$ and $\bar{z}$ from eq. 1.0.33c is

$\begin{aligned}\frac{U}{V \epsilon_0 n_0} &= 3 \sqrt{2} \theta^{5/2} \bar{z} \int_{0}^\infty dx x^{3/2} e^{-x} \\ &= 3 \sqrt{2} \theta^{5/2} \bar{z} \Gamma(5/2).\end{aligned} \hspace{\stretch{1}}(1.0.33c)$

Comparing these, we have

$\begin{aligned}\frac{1}{{\epsilon_0 n_0\sqrt{2} \theta^{5/2} \bar{z} \Gamma(5/2)}} &= 3 \frac{V}{U} \\ &= \frac{2}{P},\end{aligned} \hspace{\stretch{1}}(1.0.37)$

or in this low density limit

$\begin{aligned}\boxed{P V = \frac{2}{3} U.}\end{aligned} \hspace{\stretch{1}}(1.0.38)$

High density limit

For the high density limit write $\bar{z} = e^y$ , so that the distribution takes the form

$\begin{aligned}f(\bar{z}) &= \frac{1}{ \bar{z}^{-1} e^{x} + 1} \\ &= \frac{1}{ e^{x - y} + 1}.\end{aligned} \hspace{\stretch{1}}(1.0.39)$

This can be approximated by a step function, so that

$\begin{aligned}\frac{P}{n_0 \epsilon_0}\approx \int_{0}^y \theta dx\left( (\theta x + 1)^2 - 1 \right)^{3/2} \end{aligned} \hspace{\stretch{1}}(1.0.40a)$

$\begin{aligned}\frac{U}{V \epsilon_0 n_0} \approx3 \int_{0}^\infty \theta dx \theta x (\theta x + 1)\sqrt{(\theta x + 1)^2 - 1} \end{aligned} \hspace{\stretch{1}}(1.0.40b)$

With a change of variables $u = \theta x + 1$ , we have

$\begin{aligned}\begin{aligned}\frac{P}{n_0 \epsilon_0} &\approx \int_{1}^{\theta y + 1x} du\left( u^2 - 1 \right)^{3/2} \\ &=\frac{1}{8} \left((2 \theta y (\theta y+2)-3) \sqrt{\theta y (\theta y+2)} (\theta y+1)+3 \ln \left(\theta y+\sqrt{\theta y (\theta y+2)}+1\right)\right) \\ &\approx\frac{1}{4} \left( \theta \ln \bar{z} \right)^4\end{aligned}\end{aligned} \hspace{\stretch{1}}(1.0.41a)$

$\begin{aligned}\begin{aligned}\frac{U}{V \epsilon_0 n_0} &\approx3 \int_{1}^{\theta y + 1x} (u^2 - u)\sqrt{u^2 - 1} \\ &=\frac{3}{24} \left(\sqrt{\theta y (\theta y+2)} (\theta y (2 \theta y (3 \theta y+5)-1)+3)-3 \left(\ln \left(\theta y+\sqrt{\theta y (\theta y+2)}+1\right)\right)\right) \\ &\approx\frac{3}{4} \left( \theta \ln \bar{z} \right)^4\end{aligned}\end{aligned} \hspace{\stretch{1}}(1.0.41b)$

Comparing both we have

$\begin{aligned}\frac{4}{\epsilon_0 n_0 \left( \theta \ln \bar{z} \right) } = \frac{1}{{P}} = \frac{3 V}{U},\end{aligned} \hspace{\stretch{1}}(1.0.42)$

$\begin{aligned}\boxed{P V = \frac{1}{{3}} U.}\end{aligned} \hspace{\stretch{1}}(1.0.43)$

$\begin{aligned}{\left.{{\epsilon_{\mathrm{F}}}}\right\vert}_{{n = 1/(0.01)^3}} = 6.12402 \times 10^{-35} \text{J} \times 6.24150934 \times 10^{18} \frac{\text{eV}}{\text{J}} = 3.82231 \times 10^{-16} \text{eV}\end{aligned} \hspace{\stretch{1}}(1.0.43)$

Wow. That’s pretty low!

Pressure integral

Of these the pressure integral is yields directly to Mathematica

$\begin{aligned}\begin{aligned} \int_{0}^\infty & dx\left( (\theta x + 1)^2 - 1 \right)^{3/2} e^{-x(1 + s)} \\ &=\frac{3 \theta e^{(s+1)/\theta}}{(s + 1)^2} K_2\left( \frac{s+1}{\theta } \right) \\ &=\frac{3 \sqrt{\frac{\pi }{2}} \theta ^{3/2}}{(s+1)^{5/2}}+\frac{45 \sqrt{\frac{\pi }{2}} \theta ^{5/2}}{8 (s+1)^{7/2}}+\frac{315 \sqrt{\frac{\pi }{2}} \theta ^{7/2}}{128 (s+1)^{9/2}}-\frac{945 \sqrt{\frac{\pi }{2}} \theta ^{9/2}}{1024 (s+1)^{11/2}}+\frac{31185 \sqrt{\frac{\pi }{2}} \theta ^{11/2}}{32768 (s+1)^{13/2}} + \cdots\end{aligned}\end{aligned} \hspace{\stretch{1}}(1.0.45)$

where $K_2(z)$ is a modified Bessel function [5] of the second kind as plotted in fig. 1.2.

Fig 1.2: Modified Bessel function of the second kind

Plugging this into the series for the pressure, we have

$\begin{aligned}\frac{P}{n_0 \epsilon_0}= 3 \left( \frac{k_{\mathrm{B}} T}{\epsilon_0} \right)^2\sum_{s=0}^\infty(-1)^s\frac{\left( \bar{z} e^{\epsilon_0/k_{\mathrm{B}} T} \right)^{s + 1}}{(s + 1)^2}K_2\left( (s+1) \epsilon_0/k_{\mathrm{B}} T \right).\end{aligned} \hspace{\stretch{1}}(1.0.46)$

Plotting the summands $3 (-1)^s \frac{\theta^2}{(s + 1)^2} \left( \bar{z} e^{ 1/\theta} \right)^{s + 1} K_2\left((s+1)/\theta\right)$ for $\bar{z} = 1$ in fig. 1.4 shows that this mix of exponential Bessel and quadratic terms decreases with $s$ .

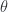Plotting this sum in fig. 1.3 numerically to 10 terms, shows that we have a function that appears roughly polynomial in $\bar{z}$ and $\theta$ .

Fig 1.3: Pressure to ten terms in z and theta

Fig 1.4: Pressure summands

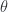For small $\bar{z}$ it can be seen graphically that there is very little contribution from anything but the $s = 0$ term of this sum. An expansion in series for a few terms in $\bar{z}$ and $\theta$ gives us

$\begin{aligned}\begin{aligned}\frac{P}{\epsilon_0 n_0}&=\sqrt{\pi} \theta^{5/2} \left(\frac{3 \bar{z}}{\sqrt{2}}-\frac{3 \bar{z}^2}{8}+\frac{\bar{z}^3}{3 \sqrt{6}}-\frac{3 \bar{z}^4}{32 \sqrt{2}}+\frac{3 \bar{z}^5}{25 \sqrt{10}}\right) \\ &+\sqrt{\pi} \theta^{7/2} \left(\frac{45 \bar{z}}{8 \sqrt{2}}\right) -\frac{45 \bar{z}^2}{128}+\frac{5 \bar{z}^3}{24 \sqrt{6}}-\frac{45 \bar{z}^4}{1024 \sqrt{2}}+\frac{9 \bar{z}^5}{200 \sqrt{10}}\\ &+\sqrt{\pi} \theta^{9/2} \left(\frac{315 \bar{z}}{128 \sqrt{2}}-\frac{315 \bar{z}^2}{4096}+\frac{35 \bar{z}^3}{1152 \sqrt{6}}-\frac{315 \bar{z}^4}{65536 \sqrt{2}}+\frac{63 \bar{z}^5}{16000 \sqrt{10}}\right).\end{aligned}\end{aligned} \hspace{\stretch{1}}(1.0.47)$

This allows a $k_{\mathrm{B}} T \ll m c^2$ and $\bar{z} \ll 1$ approximation of the pressure

$\begin{aligned}\frac{P}{\epsilon_0 n_0} = \frac{3}{2} \sqrt{2 \pi} \bar{z} \theta^{5/2}.\end{aligned} \hspace{\stretch{1}}(1.0.48)$

Number density integral

For the number density, it appears that we can evaluate the integral using integration from parts applied to eq. 1.0.30.30

$\begin{aligned}\frac{n}{n_0}= \theta\int_{0}^\infty dx\frac{3 (\theta x + 1)\sqrt{(\theta x + 1)^2 - 1} }{ \bar{z}^{-1} e^{x} + 1}=\theta\int_{0}^\infty dx\left( \frac{d}{dx} \left( (\theta x + 1)^2 - 1 \right) ^{3/2} \right)\frac{1}{ \bar{z}^{-1} e^{x} + 1}={\left.{{\theta\left( (\theta x + 1)^2 - 1 \right)^{3/2}\frac{1}{ \bar{z}^{-1} e^{x} + 1}}}\right\vert}_{{0}}^{{\infty}}-\theta\int_{0}^\infty dx\left( (\theta x + 1)^2 - 1 \right)^{3/2}\frac{ -\bar{z}^{-1} e^{x} }{ \left( \bar{z}^{-1} e^{x} + 1 \right)^2}=\theta\int_{0}^\infty dx\left( (\theta x + 1)^2 - 1 \right)^{3/2}\frac{ \bar{z} e^{-x} }{ \left( 1 + \bar{z} e^{-x} \right)^2}.\end{aligned} \hspace{\stretch{1}}(1.0.48)$

Expanding in series, gives us

$\begin{aligned}\frac{n}{n_0}=\theta\sum_{s = 0}^\infty\binom{-2}{s}\bar{z}^{s + 1} \int_{0}^\infty dx\left( (\theta x + 1)^2 - 1 \right)^{3/2} e^{-x(s + 1)}=3 \theta^2\sum_{s = 0}^\infty\binom{-2}{s}\frac{\left( \bar{z} e^{1/\theta} \right)^{s + 1}}{(s + 1)^2}K_2\left( \frac{s+1}{\theta } \right).\end{aligned} \hspace{\stretch{1}}(1.0.48)$

Here the binomial coefficient has the meaning given in the definitions of \statmechchapcite{nonIntegralBinomialSeries}, where for negative integral values of 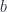$b$ we have

$\begin{aligned}\binom{b}{s}\equiv(-1)^s \frac{-b}{-b + s} \binom{-b+s}{-b}.\end{aligned} \hspace{\stretch{1}}(1.0.51)$

Expanding in series to a couple of orders in 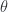$\theta$ and $\bar{z}$ we have

$\begin{aligned}\frac{n}{n_0} = \frac{\sqrt{2 \pi}}{36} \theta^{1/2} \left(\left(2 \sqrt{3} \bar{z} - 9/\sqrt{2} \right) \bar{z} +18 \right) \bar{z}+\frac{5 \sqrt{ 2 \pi}}{576} \theta^{3/2} \left(\left(4 \sqrt{3} \bar{z} - 27/\sqrt{2}\right) \bar{z} +108 \right) \bar{z}+ \cdots\end{aligned} \hspace{\stretch{1}}(1.0.52)$

To first order in 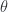$\theta$ and $\bar{z}$ this is

$\begin{aligned}\frac{n}{n_0} = \frac{1}{{2}} \sqrt{ 2 \pi } \bar{z} \theta^{1/2},\end{aligned} \hspace{\stretch{1}}(1.0.53)$

which allows a relation to pressure

$\begin{aligned}P V = 3 N (k_{\mathrm{B}} T)^2 /\epsilon_0.\end{aligned} \hspace{\stretch{1}}(1.0.54)$

It’s kind of odd seeming that this is quadratic in temperature. Is there an error?

Energy integral

Starting from eq. 1.0.30c and integrating by parts we have

$\begin{aligned}\frac{\left\langle{{\epsilon - \epsilon_0}}\right\rangle}{V \epsilon_0 n_0} &= 3 \theta^2 \int_{0}^\infty dx \frac { x (\theta x + 1)\sqrt{(\theta x + 1)^2 - 1} } { \bar{z}^{-1} e^{x} + 1 } \\ &= -\theta^2 \int_{0}^\infty dx\left( (\theta x + 1)^2 - 1 \right)^{3/2}\frac{d}{dx} \left( \frac{x} { \bar{z}^{-1} e^{x} + 1 } \right) \\ &= -\theta^2 \int_{0}^\infty dx\left( (\theta x + 1)^2 - 1 \right)^{3/2}\left( \frac{1} { \bar{z}^{-1} e^{x} + 1 } - \frac{x \bar{z}^{-1} e^{x} } { \left( \bar{z}^{-1} e^{x} + 1 \right)^2 } \right) \\ &= \theta^2 \int_{0}^\infty dx \left( (\theta x + 1)^2 - 1 \right)^{3/2} \frac{ (x - 1)\bar{z}^{-1} e^{x} - 1} { \left( \bar{z}^{-1} e^{x} + 1 \right)^2 } \\ &= \theta^2 \int_{0}^\infty dx \left( (\theta x + 1)^2 - 1 \right)^{3/2} \frac{ (x - 1)\bar{z} e^{-x} - \bar{z}^2 e^{-2 x}} { \left( 1 + \bar{z} e^{-x} \right)^2 } \\ &= \theta^2\sum_{s=0}^\infty \binom{-2}{s} \int_{0}^\infty dx \left( (\theta x + 1)^2 - 1 \right)^{3/2} \left( (x - 1)\bar{z} e^{-x} - \bar{z}^2 e^{-2 x} \right) (\bar{z} e^{-x})^s \\ &= \theta^2\sum_{s=0}^\infty \binom{-2}{s} \bar{z}^{s + 1} \int_{0}^\infty dx \left( (\theta x + 1)^2 - 1 \right)^{3/2} \left( (x - 1) e^{-x(s + 1)} - \bar{z} e^{-x(s + 2)} \right).\end{aligned} \hspace{\stretch{1}}(1.0.54)$

The integral with the factor of $x$ doesn’t have a nice closed form as before (if you consider the $K_2$ a nice closed form), but instead evaluates to a confluent hypergeometric function [6]. That integral is

$\begin{aligned}\int_0^{\infty } x \left((\theta x+1)^2-1\right)^{3/2} e^{-x (1+s)} dx = \frac{15 \sqrt{\pi } \theta^3 U\left(-\frac{3}{2},-4,\frac{2 (s+1)}{\theta }\right)}{8 (s+1)^5},\end{aligned} \hspace{\stretch{1}}(1.0.54)$

and looks like fig. 1.5. Series expansion shows that this hypergeometricU function has a $\theta^{3/2}$ singularity at the origin

Fig 1.5: Plot of HypergeometricU, and with theta^5 scaling

$\begin{aligned}U\left(-\frac{3}{2},-4,\frac{2 (s+1)}{\theta }\right)=\frac{2 \sqrt{2} \sqrt{s+1} s+2 \sqrt{2} \sqrt{s+1}}{\theta^{3/2}}+\frac{21 \sqrt{s+1}}{2 \sqrt{2} \sqrt{\theta }}+ \cdots\end{aligned} \hspace{\stretch{1}}(1.57)$

so our multiplication by $\theta^5$ brings us to zero as seen in the plot. Evaluating the complete integral yields the unholy mess

$\begin{aligned}\frac{\left\langle{{\epsilon - \epsilon_0}}\right\rangle}{V \epsilon_0 n_0} &= \sum_{s=0}^\infty \theta^2 (-1)^s (s+1) \bar{z}^{s+1} \Bigl( \\ &\frac{105 \sqrt{\pi } \theta^3 U\left(-\frac{1}{2},-4,\frac{2 (s+1)}{\theta }\right)}{16 (s+1)^5} \\ &- \frac{3 \sqrt{\pi } \theta^2 U\left(-\frac{1}{2},-2,\frac{2 (s+1)}{\theta }\right)}{2 (s+1)^3} \\ &- \frac{3 \sqrt{\pi } \theta^2 \bar{z} U\left(-\frac{1}{2},-2,\frac{2 (s+2)}{\theta }\right)}{2 (s+2)^3} \\ &+\frac{(\theta -2) (-3 \theta +2 s+2) e^{\frac{s+1}{\theta }} K_2\left(\frac{s+1}{\theta }\right)}{\theta (s+1)^2} \\ &-\frac{2 (\theta -2) e^{\frac{s+1}{\theta }} K_1\left(\frac{s+1}{\theta }\right)}{\theta (s+1)} \\ &+\frac{\bar{z} (-3 \theta +2 s+4) e^{\frac{s+2}{\theta }} K_2\left(\frac{s+2}{\theta }\right)}{(s+2)^2} \\ &-\frac{2 \bar{z} e^{\frac{s+2}{\theta }} K_1\left(\frac{s+2}{\theta }\right)}{s+2} \Bigr),\end{aligned} \hspace{\stretch{1}}(1.58)$

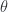to first order in $\bar{z}$ and $\theta$ this is

$\begin{aligned}\frac{\left\langle{{\epsilon - \epsilon_0}}\right\rangle}{V \epsilon_0 n_0} =\frac{9}{4} \sqrt{2 \pi} \bar{z} \theta^{7/2}.\end{aligned} \hspace{\stretch{1}}(1.59)$

Comparing pressure and energy we have for low densities (where $\bar{z} \approx 0$ )

$\begin{aligned}\frac{1}{{\epsilon_0 n_0 \sqrt{2 \pi} \bar{z} \theta^{5/2}}} = \frac{3}{2} \frac{1}{{P}} = \frac{9}{4} \theta \frac{V}{U},\end{aligned} \hspace{\stretch{1}}(1.0.60)$

$\begin{aligned}\theta P V = \frac{2}{3} U.\end{aligned} \hspace{\stretch{1}}(1.0.61)$

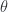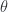It appears that I’ve picked up an extra factor of $\theta$ somewhere, but at least I’ve got the $2/3$ low density expression. Given that I’ve Taylor expanded everything anyways around $\bar{z}$ and $\theta$ this could likely have been done right from the get go, instead of dragging along the messy geometric integrals. Reworking this part of this problem like that was done above.

References

[1] Kerson Huang. Introduction to statistical physics. CRC Press, 2001.

[2] Peeter Joot. Basic statistical mechanics., chapter {Non integral binomial coefficient}. \natexlab{a}. URL http://sites.google.com/site/peeterjoot2/math2013/phy452.pdf.

[3] Peeter Joot. Basic statistical mechanics., chapter {Relativisitic density of states}. \natexlab{b}. URL http://sites.google.com/site/peeterjoot2/math2013/phy452.pdf.

[4] RK Pathria. Statistical mechanics. Butterworth Heinemann, Oxford, UK, 1996.

[5] Wolfram. BesselK, \natexlab{a}. URL http://reference.wolfram.com/mathematica/ref/BesselK.html. [Online; accessed 11-April-2013].

[6] Wolfram. HyperGeometricU, \natexlab{b}. URL http://reference.wolfram.com/mathematica/ref/HypergeometricU.html. [Online; accessed 17-April-2013].

Posted in Math and Physics Learning. | Tagged: average energy, density, distribution function, Fermi energy, Fermi gas, momentum, neutrino gas, PHY452H1S, pressure, relativistic gas, spherical coordinates, statistical mechanics | Leave a Comment »

PHY452H1S Basic Statistical Mechanics. Lecture 21: Phonon modes. Taught by Prof. Arun Paramekanti

Posted by peeterjoot on April 4, 2013

[Click here for a PDF of this post with nicer formatting (especially if my latex to wordpress script has left FORMULA DOES NOT PARSE errors.)]

Disclaimer

Peeter’s lecture notes from class. May not be entirely coherent.

These are notes for the last class, which included a lot of discussion not captured by this short set of notes (as well as slides which were not transcribed).

Phonon modes

If we model a solid as a set of interconnected springs, as in fig. 1.1, then the potentials are of the form

Fig 1.1: Solid oscillator model

$\begin{aligned}V = \frac{1}{{2}} C \sum_n \left( {u_n - u_{n+1}} \right)^2,\end{aligned} \hspace{\stretch{1}}(1.2.1)$

with kinetic energies

$\begin{aligned}K = \sum_n \frac{p_n^2}{2m}.\end{aligned} \hspace{\stretch{1}}(1.2.2)$

It’s possible to introduce generalized forces

$\begin{aligned}F = -\frac{\partial {V}}{\partial {u_n}}\end{aligned} \hspace{\stretch{1}}(1.2.3)$

Can differentiate

$\begin{aligned}m \frac{d^2 u_n}{dt^2} = - C \left( { u_n - u_{n+1}} \right)- C \left( { u_n - u_{n-1}} \right)\end{aligned} \hspace{\stretch{1}}(1.2.4)$

Assuming a Fourier representation

$\begin{aligned}u_n = \sum_k \tilde{u}(k) e^{i k n a},\end{aligned} \hspace{\stretch{1}}(1.2.5)$

we find

$\begin{aligned}m \frac{d^2 \tilde{u}(k)}{dt^2} = - 2 C \left( { 1 - \cos k a} \right)\tilde{u}(k)\end{aligned} \hspace{\stretch{1}}(1.2.6)$

This looks like a harmonic oscillator with

$\begin{aligned}\omega(k) = \sqrt{ \frac{2 C}{m} ( 1 - \cos k a)}.\end{aligned} \hspace{\stretch{1}}(1.2.7)$

This is plotted in fig. 1.2. In particular note that for for $k a \ll 1$ we can use a linear approximation

Fig 1.2: Angular frequency of solid oscillator model

$\begin{aligned}\omega(k) \approx \sqrt{ \frac{C}{m} a^2 } \left\lvert {k} \right\rvert.\end{aligned} \hspace{\stretch{1}}(1.2.8)$

Experimentally, looking at specific for a complex atomic structure like Gold, we find for example good fit for a model such as

$\begin{aligned}C \sim \underbrace{A T}_{\text{Contribution due to electrons.}}+ \underbrace{B T^3}_{\text{Contribution due to phonon like modes where there are linear energy momenum relations.}}.\end{aligned} \hspace{\stretch{1}}(1.2.9)$

Posted in Math and Physics Learning. | Tagged: harmonic oscillator, phonon modes, PHY452H1S, statistical mechanics | Leave a Comment »

PHY452H1S Basic Statistical Mechanics. Lecture 20: Bosons. Taught by Prof. Arun Paramekanti

Posted by peeterjoot on April 2, 2013

[Click here for a PDF of this post with nicer formatting (especially if my latex to wordpress script has left FORMULA DOES NOT PARSE errors.)]

Disclaimer

Peeter’s lecture notes from class. May not be entirely coherent.

Bosons

In order to maintain a conservation of particles in a Bose condensate as we decrease temperature, we are forced to change the chemical potential to compensate. This is illustrated in fig. 1.1.

Fig 1.1: Chemical potential in Bose condensation region

Bose condensatation occurs for $T < T_{\mathrm{BEC}}$ . At this point our number density becomes (except at $\mathbf{k} = 0$ )

$\begin{aligned}n(\mathbf{k}) = \frac{1}{{e^{\beta \epsilon_\mathbf{k}} - 1}}.\end{aligned} \hspace{\stretch{1}}(1.2.1)$

Except for $\mathbf{k} = 0$ , $n(\mathbf{k})$ is well defined, and not described by this distribution. We are forced to say that

$\begin{aligned}N = N_0 + \sum_{\mathbf{k} \ne 0} n(\mathbf{k}) = N_0 + V\int \frac{d^3 \mathbf{k}}{(2 \pi)^3} \frac{1}{{ e^{\beta \epsilon_\mathbf{k}} - 1 }}.\end{aligned} \hspace{\stretch{1}}(1.2.1)$

Introducing the density of states, our density is

$\begin{aligned}\rho = \rho_0 + \int_0^\infty d\epsilon \frac{N(\epsilon)}{e^{\beta \epsilon} - 1 },\end{aligned} \hspace{\stretch{1}}(1.2.3)$

where

$\begin{aligned}N(\epsilon) = \frac{1}{{4 \pi^2}} \left( \frac{2m}{\hbar} \right)^{3/2} \epsilon^{1/2}.\end{aligned} \hspace{\stretch{1}}(1.2.4)$

We worked out last time that

$\begin{aligned}\rho = \rho_0 + \rho \left( \frac{T}{T_{\mathrm{BEC}}} \right)^{3/2},\end{aligned} \hspace{\stretch{1}}(1.2.4)$

$\begin{aligned}\rho_0 = \rho \left( 1 - \left( \frac{T}{T_{\mathrm{BEC}}} \right) ^{3/2} \right).\end{aligned} \hspace{\stretch{1}}(1.2.6)$

This is plotted in fig. 1.2.

Fig 1.2: Density variation with temperature for Bosons

$\begin{aligned}\rho_0 = \frac{N_{\mathbf{k} = 0}}{V}.\end{aligned} \hspace{\stretch{1}}(1.7)$

For $T \ge T_{\mathrm{BEC}}$ , we have $\rho_0 = 0$ . This condensation temperature is

$\begin{aligned}T_{\mathrm{BEC}} \propto \rho^{2/3}.\end{aligned} \hspace{\stretch{1}}(1.8)$

This is plotted in fig. 1.3.

Fig 1.3: Temperature vs pressure demarkation by T_BEC curve

There is a line for each density that marks the boundary temperature for which we have or do not have this condensation phenomina where $\mathbf{k} = 0$ states start filling up.

Specific heat: $T < T_{\mathrm{BEC}}$

$\begin{aligned}\frac{E}{V} &= \int \frac{d^3 \mathbf{k}}{(2 \pi)^3} \frac{1}{{ e^{\beta \hbar^2 k^2/2m} - 1}}\frac{\hbar^2 k^2}{2m} \\ &= \int_0^\infty d\epsilon N(\epsilon) \frac{1}{{ e^{\beta \epsilon} - 1 }} \epsilon \\ &\propto \int_0^\infty d\epsilon \frac{\epsilon^{3/2}}{ e^{\beta \epsilon} - 1 } \\ &\propto \left( k_{\mathrm{B}} T \right)^{5/2},\end{aligned} \hspace{\stretch{1}}(1.9)$

so that

$\begin{aligned}\frac{C}{V} \propto \left( k_{\mathrm{B}} T \right)^{3/2}.\end{aligned} \hspace{\stretch{1}}(1.10)$

Compare this to the classical and Fermionic specific heat as plotted in fig. 1.4.

Fig 1.4: Specific heat for Bosons, Fermions, and classical ideal gases

One can measure the specific heat in this Bose condensation phenomina for materials such as Helium-4 (spin 0). However, it turns out that Helium-4 is actually quite far from an ideal Bose gas.

Photon gas

A system that is much closer to an ideal Bose gas is that of a gas of photons. To a large extent, photons do not interact with each other. This allows us to calculate black body phenomina and the low temperature (cosmic) background radiation in the universe.

An important distinction between a photon sea and some of these other systems is that the photon number is actually not fixed.

Photon numbers are not “conserved”.

If a photon interacts with an atom, it can impart energy and disappear. An excited atom can emit a photon and change its energy level. In a thermodynamic system we can generally expect that introducing heat will generate more photons, whereas a cold sink will tend to generate fewer photons.

We have a few special details that distinguish photons that we’ll have to consider.

spin 1.
massless, moving at the speed of light.
have two polarization states.

Because we do not have a constraint on the number of particles, we essentially have no chemical potential, even in the grand canonical scheme.

Writing

$\begin{aligned}\lambda = \left\{\begin{array}{l l}+1 & \quad \mbox{Right circular polarization} \\ -1 & \quad \mbox{Left circular polarization}\end{array}\right.\end{aligned} \hspace{\stretch{1}}(1.11)$

Our number density, since we have no chemical potential, is of the form

$\begin{aligned}n_{\mathbf{k}, \lambda}= \frac{1}{{e^{\beta \epsilon_{\mathbf{k}, \lambda}} - 1 }},\end{aligned} \hspace{\stretch{1}}(1.12)$

Observe that the average number of photons in this system is temperature dependent. Because this chemical potential is not there, it can be quite easy to work out a number of the thermodynamic results.

Photon average energy density

We’ll now calculate the average energy density of the photons. The energy of a single photon is

$\begin{aligned}\epsilon_{\mathbf{k}, \lambda} = \hbar c k = \hbar \omega,\end{aligned} \hspace{\stretch{1}}(1.2.13)$

so that the average energy density is

$\begin{aligned}\frac{E}{V} &= \sum_{\mathbf{k}, \lambda} \frac{1}{{ e^{ \beta \epsilon_\mathbf{k}} - 1}} \epsilon_\mathbf{k}\rightarrow\underbrace{2}_{\text{number of polarizations}}\int \frac{d^3 \mathbf{k}}{(2 \pi)^3}\frac{ \hbar c k}{ e^{ \beta \epsilon_\mathbf{k}} - 1} \\ &= 2 \int_0^\infty d\epsilon \underbrace{\frac{1}{{(2 \pi)^3}} 4 \pi \frac{\epsilon^2}{(\hbar c)^3} }_{\text{Photon density of states}}\frac{\epsilon}{e^{\beta \epsilon} - 1} \\ &= \frac{1}{{\pi^2}} \frac{1}{{ (\hbar c)^3 }} \int_0^\infty d\epsilon \frac{\epsilon^3}{e^{\beta \epsilon} - 1}\end{aligned} \hspace{\stretch{1}}(1.2.13)$

Mathematica tells us that this integral is

$\begin{aligned}\int_0^\infty d\epsilon \frac{\epsilon^3}{e^{\beta \epsilon} - 1} =\frac{\pi ^4}{15 \beta ^4},\end{aligned} \hspace{\stretch{1}}(1.2.13)$

for an end result of

$\begin{aligned}\frac{E}{V} =\frac{\pi^2}{15} \frac{1}{{(\hbar c)^3}} \left( k_{\mathrm{B}} T \right)^4.\end{aligned} \hspace{\stretch{1}}(1.2.13)$

Phonons and other systems

There is a very similar phenomina in matter. We can discuss lattice vibrations in a solid. These are called phonon modes, and will have the same distribution function where the only difference is that the speed of light is replaced by the speed of the sound wave in the solid. Once we understand the photon system, we are able to look at other Bose distributions such as these phonon systems. We’ll touch on this very briefly next time.

Posted in Math and Physics Learning. | Tagged: average energy density, Bose condensation, chemical potential, density of states, energy density, Helium-4, phonon, photon gas, PHY452H1S, Polarization, specific heat, statistical mechanics | Leave a Comment »

« Previous Entries

	Determining the alig… on C structure alignment pad…
	Manas shetty on Cartesian to spherical change…
	peeterjoot on Derivative recurrence relation…
	Daniel Pires on Derivative recurrence relation…
	peeterjoot on Curious problem using the vari…

Peeter Joot's (OLD) Blog.

Math, physics, perl, and programming obscurity.

Categories

Archives

Recent Posts

Meta

Recent Comments

People not reading this blog: 7,179,979,522 minus:

Subscribe

Posts Tagged ‘statistical mechanics’

Final version of my phy452.pdf notes posted

Large volume Fermi gas density

Question: Large volume Fermi gas density (2013 final exam pr 1)

Answer

A dumb expansion of the Fermi-Dirac grand partition function

References

Ultra relativisitic spin zero condensation temperature

Question: Ultra relativisitic spin zero condensation temperature (2013 final exam pr 2)

Answer

References

Summary of statistical mechanics relations and helpful formulas (cheat sheet fodder)

Low temperature Fermi gas chemical potential

Question: Low temperature Fermi gas chemical potential

Answer

References

A final pre-exam update of my notes compilation for ‘PHY452H1S Basic Statistical Mechanics’, Taught by Prof. Arun Paramekanti

Relativisitic Fermi gas

Question: Relativisitic Fermi gas ([1], pr 9.3)

Answer

References

PHY452H1S Basic Statistical Mechanics. Lecture 21: Phonon modes. Taught by Prof. Arun Paramekanti

Disclaimer

Phonon modes

PHY452H1S Basic Statistical Mechanics. Lecture 20: Bosons. Taught by Prof. Arun Paramekanti

Disclaimer

Bosons