April 2024
M	T	W	T	F	S	S
1	2	3	4	5	6	7
8	9	10	11	12	13	14
15	16	17	18	19	20	21
22	23	24	25	26	27	28
29	30

Posts Tagged ‘Bose condensate’

Final version of my phy452.pdf notes posted

Posted by peeterjoot on September 5, 2013

I’d intended to rework the exam problems over the summer and make that the last update to my stat mech notes. However, I ended up studying world events and some other non-mainstream ideas intensively over the summer, and never got around to that final update.

Since I’m starting a new course (condensed matter) soon, I’ll end up having to focus on that, and have now posted a final version of my notes as is.

Since the last update the following additions were made

September 05, 2013 Large volume fermi gas density

May 30, 2013 Bernoulli polynomials and numbers and Euler-MacLauren summation

May 09, 2013 Bose gas specific heat above condensation temperature

May 09, 2013 A dumb expansion of the Fermi-Dirac grand partition function

April 30, 2013 Ultra relativistic spin zero condensation temperature

April 30, 2013 Summary of statistical mechanics relations and helpful formulas

April 24, 2013 Low temperature Fermi gas chemical potential

Posted in Math and Physics Learning. | Tagged: average, Bernoulli number, Bernoulli polynomial, binomial distribution, Bose condensate, Bose gas, Bosons, canonical ensemble, Central limit theorem, cheat sheet, chemical potential, classical limit, density of states, ergodic, Euler-MacLauren summation, Fermi energy, Fermi gas, Fermi-Dirac, Fermions, fugacity, Generating function, grand canonical ensemble, grand canonical partition function, ground state, Hamilton's equations, Handy mathematics, ideal gas, large volume, Liouville's theorem, low temperature, Maxwell distribution, Microstates, number density, PHY452H1S, Quantum free particle in a box, Radius of gyration of a 3D polymer, random walk, specific heat, spin, statistical mechanics, statistics, Statistics mechanics, surface with binding sites, thermodynamics, ultra relativistic gas, Velocity, zeta function | Leave a Comment »

Ultra relativisitic spin zero condensation temperature

Posted by peeterjoot on April 30, 2013

[Click here for a PDF of this post with nicer formatting (especially if my latex to wordpress script has left FORMULA DOES NOT PARSE errors.)]

Here’s a bash at one of the exam questions, where I get the time to think things through properly. I think I did something like this on the exam itself, but may have also made some arithmetic errors.

Question: Ultra relativisitic spin zero condensation temperature (2013 final exam pr 2)

Consider a Bose gas with particles having no spin and obeying an ultra relativisitic dispersion $E_\mathbf{k} = c \left\lvert {\mathbf{k}} \right\rvert$ . Unlike photons or phonons, these particles are {\bf conserved}, and hence we must determine the chemical potential $\mu$ which fixes their density. Working in three dimensions, show whether or not these particles will exhibit Bose condensation, and find $T_c$ if it is nonzero.

Answer

For the number of particles in the gas, as with photons, we still have

$\begin{aligned}\left\langle{{N}}\right\rangle = \sum_\mathbf{k} \frac{1}{{z^{-1} e^{\beta \epsilon_\mathbf{k}} - 1}}= \frac{1}{{z^{-1} - 1}}+ \sum_{\mathbf{k} \ne 0} \frac{1}{{z^{-1} e^{\beta \epsilon_\mathbf{k}} - 1}}.\end{aligned} \hspace{\stretch{1}}(1.1)$

As in the discussion of low velocity particles in [1] section 7.1, the ground state term has been split out, before making any continuum approximation of the sum over the energetic states.

Writing

$\begin{aligned}\left\langle{{N}}\right\rangle = N_0 + N_e,\end{aligned} \hspace{\stretch{1}}(1.0.2)$

where the number of particles in the ground state is chemical potential and temperature dependent

$\begin{aligned}N_0 = \frac{z}{1 - z}.\end{aligned} \hspace{\stretch{1}}(1.0.3)$

We proceed with the continuum approximation for the number of particles in the energetic states

$\begin{aligned}N_e &= \sum_{\mathbf{k} \ne 0} \frac{1}{{z^{-1} e^{\beta \epsilon_\mathbf{k}} - 1}} \\ &\sim V \int \frac{d^3 \mathbf{k}}{(2 \pi)^3}\frac{1}{{z^{-1} e^{\beta \epsilon_\mathbf{k}} - 1}} \\ &= \frac{4 \pi V}{(2 \pi)^3} \int_0^\infty k^2 dk\frac{1}{{z^{-1} e^{\beta c k} - 1}} \\ &= \frac{V}{2 \pi^2} \left( { \frac{1}{{\beta c}} } \right)^3\int_0^\infty x^2 dx\frac{1}{{z^{-1} e^{x} - 1}} \\ &= \frac{V}{2 \pi^2} \left( { \frac{1}{{\beta c}} } \right)^3\Gamma(3) g_3(z).\end{aligned} \hspace{\stretch{1}}(1.0.3)$

So we have

$\begin{aligned}N_e=\frac{V}{\pi^2} \left( { \frac{k_{\mathrm{B}} T}{c} } \right)^3g_3(z)\le \frac{V}{\pi^2} \left( { \frac{k_{\mathrm{B}} T}{c} } \right)^3\zeta(3).\end{aligned} \hspace{\stretch{1}}(1.0.5)$

Note that $\zeta(3) \approx 1.20206$ , a fixed number. The key feature of Bose condensation remains. There is a finite limit to the number of particles that can be in the energetic state at a given temperature and volume. Any remaining particles are forced into the ground state.

In general the number of particles in the ground state is

$\begin{aligned}N_0 = N - \frac{V}{\pi^2} \left( { \frac{k_{\mathrm{B}} T}{c} } \right)^3g_3(z),\end{aligned} \hspace{\stretch{1}}(1.0.6)$

and we will necessarily have particles in this state if

$\begin{aligned}N - \frac{V}{\pi^2} \left( { \frac{k_{\mathrm{B}} T}{c} } \right)^3\zeta(3) > 0.\end{aligned} \hspace{\stretch{1}}(1.0.7)$

That temperature threshold $T \le T_c$ is the Bose condensation temperature

$\begin{aligned}\boxed{k_{\mathrm{B}} T_c = c \left( { \frac{n \pi^2}{\zeta(3)} } \right)^{1/3}.}\end{aligned} \hspace{\stretch{1}}(1.0.8)$

With $n = N/V$ , $n_0 = N_0/V$ , we have for the ground state average number density

$\begin{aligned}n_0 = n\left( 1 - \frac{g_3(z)}{\zeta(3)} \left( { \frac{T}{T_c} } \right)^3 \right)\end{aligned} \hspace{\stretch{1}}(1.0.9)$

This is plotted in fig. 1.1.

Fig 1.1: Ratio of ground state number density to total number density

From the figure it appears that the notion of any sort of absolute condensation temperature is an approximation. We can start having particles go into the ground state at higher temperatures than $T_c$ , but once the chemical potential starts approaching zero, that temperature for which we start having particles in the ground state approaches $T_c$ . The key takeout idea appears to be, once the temperature does drop below $T_c$ , we necessarily start having a non-zero ground state population, and as the temperature drops more and more, the ratio of the number of particles in the ground state relative to the total approaches unity (all particles are forced into the ground state).

References

[1] RK Pathria. Statistical mechanics. Butterworth Heinemann, Oxford, UK, 1996.

Posted in Math and Physics Learning. | Tagged: average number density, Bose condensate, ground state number density, PHY452H1S, statistical mechanics, ultra relativisitic gas, zeta function | Leave a Comment »

A final pre-exam update of my notes compilation for ‘PHY452H1S Basic Statistical Mechanics’, Taught by Prof. Arun Paramekanti

Posted by peeterjoot on April 22, 2013

Here’s my third update of my notes compilation for this course, including all of the following:

April 21, 2013 Fermi function expansion for thermodynamic quantities

April 20, 2013 Relativistic Fermi Gas

April 10, 2013 Non integral binomial coefficient

April 10, 2013 energy distribution around mean energy

April 09, 2013 Velocity volume element to momentum volume element

April 04, 2013 Phonon modes

April 03, 2013 BEC and phonons

April 03, 2013 Max entropy, fugacity, and Fermi gas

April 02, 2013 Bosons

April 02, 2013 Relativisitic density of states

March 28, 2013 Bosons

plus everything detailed in the description of my previous update and before.

Posted in Math and Physics Learning. | Tagged: average energy, average energy density, average number of particles, average occupancy, BEC temperature, binomial coefficient, binomial series, Boltzmann factor, Bose condensate, Bose condensation, Bose-Einstein condensate, Boson, canonical ensemble, chemical potential, configurations, constraint, delta function, density, density of states, distribution function, energy, energy density, ensemble, entropy, extreme relativistic gas, factorial, Fermi energy, Fermi gas, Fermi-Dirac function, Fermion, fugacity, Gamma function, Gibbs entropy, grand canonical ensemble, harmonic oscillator, Helium-4, jacobian, Lagrange multiplier, mean energy, microstate, momentum, momentum space volume element, neutrino gas, neutron star, nucleon, number density, occupation number, phonon, phonon modes, photon, photon gas, PHY452H1S, Polarization, pressure, probability, relativistic, relativistic gas, special relativity, specific heat, spherical coordinates, statistical mechanics, Taylor expansion, temperature, velocity space volume element, volume, zeta function | 1 Comment »

PHY452H1S Basic Statistical Mechanics. Lecture 19: Bosons. Taught by Prof. Arun Paramekanti

Posted by peeterjoot on March 28, 2013

[Click here for a PDF of this post with nicer formatting (especially if my latex to wordpress script has left FORMULA DOES NOT PARSE errors.)]

Disclaimer

Peeter’s lecture notes from class. May not be entirely coherent.

Fermions summary

We’ve considered a momentum sphere as in fig. 1.1, and performed various appromations of the occupation sums fig. 1.2.

Fig 1.1: Summation over momentum sphere

Fig 1.2: Fermion occupation

$\begin{aligned}\epsilon \sim T^2\end{aligned} \hspace{\stretch{1}}(1.0.1.1)$

$\begin{aligned}C \sim T\end{aligned} \hspace{\stretch{1}}(1.0.1.1)$

$\begin{aligned}P \sim \text{constant}\end{aligned} \hspace{\stretch{1}}(1.0.1.1)$

The physics of Fermi gases has an extremely wide range of applicability. Illustrating some of this range, here are some examples of Fermi temperatures (from 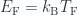$E_{\mathrm{F}} = k_{\mathrm{B}} T_{\mathrm{F}}$ )

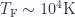
Electrons in copper: $T_{\mathrm{F}} \sim 10^4 \mbox{K}$
Neutrons in neutron star: $T_{\mathrm{F}} \sim 10^7 - 10^8 \mbox{K}$
Ultracold atomic gases: $T_{\mathrm{F}} \sim (10 - 100) \mbox{n K}$

Bosons

We’d like to work with a fixed number of particles, but the calculations are hard, so we move to the grand canonical ensemble

$\begin{aligned}n_{\mathrm{B}}(\mathbf{k}) = \frac{1}{{ e^{\beta(\epsilon_\mathbf{k} - \mu)} - 1 }}\end{aligned} \hspace{\stretch{1}}(1.2)$

Again, we’ll consider free particles with energy as in fig. 1.3, or

$\begin{aligned}\epsilon_\mathbf{k} = \frac{\hbar^2 k^2}{2 m}.\end{aligned} \hspace{\stretch{1}}(1.3)$

Fig 1.3: Free particle energy momentum distribution

Again introducing fugacity 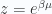$z = e^{\beta \mu}$ , we have

$\begin{aligned}n_{\mathrm{B}}(\mathbf{k}) = \frac{1}{{ z^{-1} e^{\beta \epsilon_\mathbf{k}} - 1 }}\end{aligned} \hspace{\stretch{1}}(1.4)$

We’ll consider systems for which

$\begin{aligned}N = \sum_\mathbf{k} n_{\mathrm{B}}(\mathbf{k}) = \text{fixed}\end{aligned} \hspace{\stretch{1}}(1.5)$

Observe that at large energies we have

$\begin{aligned}n_{\mathrm{B}}(\text{large} \, \mathbf{k}) \sim z e^{-\beta \epsilon_\mathbf{k}}\end{aligned} \hspace{\stretch{1}}(1.6)$

For small energies

$\begin{aligned}n_{\mathrm{B}}(\mathbf{k} \rightarrow 0) \sim \frac{1}{{z^{-1} - 1}} = \frac{z}{1 - z}\end{aligned} \hspace{\stretch{1}}(1.7)$

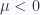Observe that we require $z < 1$ (or $\mu < 0$ ) so that the number distribution is strictly positive for all energies. This tells us that the fugacity is a function of temperature, but there will be a point at which it must saturate. This is illustrated in fig. 1.4.

Fig 1.4: Density times cubed thermal de Broglie wavelength

Let’s calculate this density (assumed fixed for all temperatures)

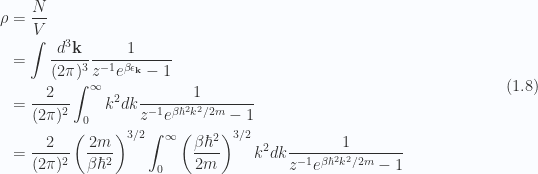
$\begin{aligned}\rho &= \frac{N}{V} \\ &= \int \frac{d^3 \mathbf{k}}{(2 \pi)^3} \frac{1}{{z^{-1} e^{\beta \epsilon_\mathbf{k}} -1 }} \\ &= \frac{2}{(2 \pi)^2} \int_0^\infty k^2 dk \frac{1}{{z^{-1} e^{\beta \hbar^2 k^2/2m} -1 }} \\ &= \frac{2}{(2 \pi)^2} \left( \frac {2 m} {\beta \hbar^2} \right)^{3/2}\int_0^\infty \left( \frac {\beta \hbar^2} {2 m} \right)^{3/2}k^2 dk \frac{1}{{z^{-1} e^{\beta \hbar^2 k^2/2m} -1 }}\end{aligned} \hspace{\stretch{1}}(1.8)$

With the substitution

$\begin{aligned}x^2 = \beta \frac{\hbar^2 k^2}{2m},\end{aligned} \hspace{\stretch{1}}(1.9)$

we find

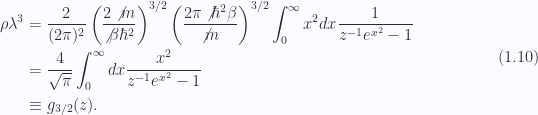
$\begin{aligned}\rho \lambda^3 &= \frac{2}{(2 \pi)^2} \left( \frac {2 \not{{m}}} {\not{{\beta \hbar^2}}} \right)^{3/2}\left( \frac{ 2 \pi \not{{\hbar^2 \beta}}}{\not{{m}}} \right)^{3/2}\int_0^\infty x^2 dx \frac{1}{{z^{-1} e^{x^2} -1 }} \\ &= \frac{4}{\sqrt{\pi}} \int_0^\infty dx \frac{x^2}{z^{-1} e^{x^2} - 1 } \\ &\equiv g_{3/2}(z).\end{aligned} \hspace{\stretch{1}}(1.10)$

This implicitly defines a relationship for the fugacity as a function of temperature 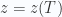$z = z(T)$ .

It can be shown that

$\begin{aligned}g_{3/2}(z) = z + \frac{z^2}{2^{3/2}}+ \frac{z^3}{3^{3/2}}+ \cdots\end{aligned} \hspace{\stretch{1}}(1.11)$

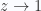As $z \rightarrow 1$ we end up with a zeta function, for which we can look up the value

$\begin{aligned}g_{3/2}(z \rightarrow 1) = \sum_{n = 1}^\infty \frac{1}{{n^{3/2}}} = \zeta(3/2) \approx 2.612\end{aligned} \hspace{\stretch{1}}(1.12)$

where the Riemann zeta function is defined as

$\begin{aligned}\zeta(s) = \sum_{ n = 1 } \frac{1}{{n^s}}.\end{aligned} \hspace{\stretch{1}}(1.13)$

$\begin{aligned}g_{3/2}(z) = \rho \lambda^3\end{aligned} \hspace{\stretch{1}}(1.14)$

At high temperatures we have

$\begin{aligned}\rho \lambda^3 \rightarrow 0\end{aligned} \hspace{\stretch{1}}(1.15)$

(as $T$ does down, $\rho \lambda^3$ goes up)

Looking at 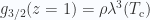$g_{3/2}(z = 1) = \rho \lambda^3(T_{\mathrm{c}})$ leads to

$\begin{aligned}\boxed{k_{\mathrm{B}} T_{\mathrm{c}} = \left( \frac{\rho}{\zeta(3/2)} \right)^{2/3} \frac{ 2 \pi \hbar^2}{m}.}\end{aligned} \hspace{\stretch{1}}(1.16)$

How do I satisfy number conservation?

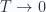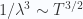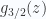We have a problem here since as $T \rightarrow 0$ the $1/\lambda^3 \sim T^{3/2}$ term in $\rho$ above drops to zero, yet $g_{3/2}(z)$ cannot keep increasing without bounds to compensate and keep the density fixed. The way to deal with this was worked out by

Bose (1924) for photons (examining statistics for symmetric wave functions).
Einstein (1925) for conserved particles.

To deal with this issue, we (somewhat arbitrarily, because we need to) introduce a non-zero density for 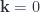$\mathbf{k} = 0$ . This is an adjustment of the approximation so that we have

$\begin{aligned}\sum_{\mathbf{k}} \rightarrow \int \frac{d^3 \mathbf{k}}{(2 \pi)^3} \qquad \mbox{Except around k = 0},\end{aligned} \hspace{\stretch{1}}(1.17)$

as in fig. 1.5, so that

Fig 1.5: Momentum sphere with origin omitted

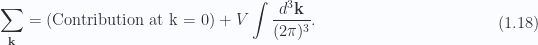
$\begin{aligned}\sum_\mathbf{k} = \left( \mbox{Contribution at k = 0} \right)+ V \int \frac{d^3 \mathbf{k}}{(2 \pi)^3}.\end{aligned} \hspace{\stretch{1}}(1.18)$

Given this, we have

$\begin{aligned}N= N_{\mathbf{k} = 0}+ V \int \frac{d^3 \mathbf{k}}{(2 \pi)^3} n_{\mathrm{B}}(\mathbf{k})\end{aligned} \hspace{\stretch{1}}(1.19)$

We can illustrate this as in fig. 1.6.

Fig 1.6: Boson occupation vs momentum

$\begin{aligned}\rho= \rho_{\mathbf{k} = 0}+ \frac{1}{{\lambda^3}} g_{3/2}(z)= \rho_{\mathbf{k} = 0}+ \frac{ \lambda(T_{\mathrm{c}}) }{ \lambda(T)}\frac{1}{{ \lambda^3(T_{\mathrm{c}})}}g_{3/2}(z)\end{aligned} \hspace{\stretch{1}}(1.20)$

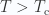At $T > T_{\mathrm{c}}$ we have $\rho_{\mathbf{k} = 0}$ , whereas at $T < T_{\mathrm{c}}$ we must introduce a non-zero density if we want to be able to keep a constant density constraint.

Posted in Math and Physics Learning. | Tagged: Bose condensate, Boson, density, fugacity, occupation number, PHY452H1S, statistical mechanics, zeta function | Leave a Comment »

	Determining the alig… on C structure alignment pad…
	Manas shetty on Cartesian to spherical change…
	peeterjoot on Derivative recurrence relation…
	Daniel Pires on Derivative recurrence relation…
	peeterjoot on Curious problem using the vari…

Peeter Joot's (OLD) Blog.

Math, physics, perl, and programming obscurity.

Categories

Archives

Recent Posts

Meta

Recent Comments

People not reading this blog: 7,179,979,522 minus:

Subscribe