[Click here for a PDF of this post with nicer formatting]
Reading.
Still covering chapter 1 material from the text [1].
Covering Professor Poppitz’s lecture notes: nonrelativistic limit of boosts (33); number of parameters of Lorentz transformations (34-35); introducing four-vectors, the metric tensor, the invariant “dot-product and SO(1,3) (36-40); the Poincare group (41); the convenience of “upper” and “lower” indices (42-43); tensors (44)
The Special Orthogonal group (for Euclidean space).
Lorentz transformations are like “rotations” for  that preserve
that preserve  . There are 6 continuous parameters:
. There are 6 continuous parameters:
\begin{itemize}
\item 3 rotations in  space
space
\item 3 “boosts” in  or
or 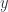 or
or  .
.
\end{itemize}
For rotations of space we talk about a group of transformations of 3D Euclidean space, and call this the  group. Here
group. Here 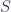 is for Special,
is for Special,  for Orthogonal, and
for Orthogonal, and  for the dimensions.
for the dimensions.
For a transformed vector in 3D space we write

Here  is an orthogonal
is an orthogonal  matrix, and has the property
matrix, and has the property

Taking determinants, we have

and since  , we have
, we have

so our determinant must be

We work with the positive case only, avoiding the transformations that include reflections.
The Unitary condition  is an indication that the inner product is preserved. Observe that in matrix form we can write the inner product
is an indication that the inner product is preserved. Observe that in matrix form we can write the inner product

For a transformed vector  , we have
, we have  , and
, and

The Special Orthogonal group (for spacetime).
This generalizes to Lorentz boosts! There are two differences
\begin{enumerate}
\item Lorentz transforms should be  not
not  and act in
and act in  , and NOT
, and NOT  .
.
\item They should leave invariant NOT  , but
, but  .
.
\end{enumerate}
Don’t get confused that I demanded  rather than
rather than  . Expansion of this (squared) interval, provides just this four vector dot product and its invariance condition
. Expansion of this (squared) interval, provides just this four vector dot product and its invariance condition

Observe that we have the sum of two invariants plus our new cross term, so this cross term, (-2 times our dot product to be defined), must also be an invariant.
Introduce the four vector

Or  .
.
We will also write

Our inner product is

Introduce the  matrix
matrix

This is called the Minkowski spacetime metric.
Then

\paragraph{Einstein summation convention}. Whenever indexes are repeated that are assumed to be summed over.
We also write



Our inner product

Under Lorentz boosts, we have

where

(for x-direction boosts)

But  must be such that
must be such that  is invariant. i.e.
is invariant. i.e.

This implies

Such  ‘s are called “pseudo-orthogonal”.
‘s are called “pseudo-orthogonal”.
Lorentz transformations are represented by the set of all  pseudo-orthogonal matrices.
pseudo-orthogonal matrices.
In symbols

Just as before we can take the determinant of both sides. Doing so we have

The  terms cancel, and since
terms cancel, and since  , this leaves us with
, this leaves us with  , or
, or

We take the  case only, so that the transformations do not change orientation (no reflection in space or time). This set of transformation forms the group
case only, so that the transformations do not change orientation (no reflection in space or time). This set of transformation forms the group

Special orthogonal, one time, 3 space dimensions.
Einstein relativity can be defined as the “laws of physics that leave four vectors invariant in the

symmetry group.
Here  is the group of translations in spacetime with 4 continuous parameters. The complete group of transformations that form the group of relativistic physics has
is the group of translations in spacetime with 4 continuous parameters. The complete group of transformations that form the group of relativistic physics has  continuous parameters.
continuous parameters.
This group is called the Poincare group of symmetry transforms.
More notation
Our inner product is written

but this is very cumbersome. The convenient way to write this is instead

where

Note: A check that we should always be able to make. Indexes that are not summed over should be conserved. So in the above we have a free  on the LHS, and should have a non-summed
on the LHS, and should have a non-summed  index on the RHS too (also lower matching lower, or upper matching upper).
index on the RHS too (also lower matching lower, or upper matching upper).
Non-matched indexes are bad in the same sort of sense that an expression like

isn’t well defined (assuming a vector space  and not a multivector Clifford algebra that is;)
and not a multivector Clifford algebra that is;)
Example explicitly:

We would not have objects of the form

for example. This is not a Lorentz invariant quantity.
\paragraph{Lorentz scalar example:} 
\paragraph{Lorentz vector example:} 
This last is also called a rank-1 tensor.
Lorentz rank-2 tensors: ex: 
or other 2-index objects.
Why in the world would we ever want to consider two index objects. We aren’t just trying to be hard on ourselves. Recall from classical mechanics that we have a two index object, the inertial tensor.
In mechanics, for a rigid body we had the energy

The inertial tensor was this object

or for a continuous body

In electrostatics we have the quadrupole tensor, … and we have other such objects all over physics.
Note that the energy  of the body above cannot depend on the coordinate system in use. This is a general property of tensors. These are object that transform as products of vectors, as
of the body above cannot depend on the coordinate system in use. This is a general property of tensors. These are object that transform as products of vectors, as  does.
does.
We call  a rank-2 3-tensor. rank-2 because there are two indexes, and 3 because the indexes range from
a rank-2 3-tensor. rank-2 because there are two indexes, and 3 because the indexes range from  to
to  .
.
The point is that tensors have the property that the transformed tensors transform as

Another example: the completely antisymmetric rank 3, 3-tensor

Dynamics
In Newtonian dynamics we have

An equation of motion should be expressed in terms of vectors. This equation is written in a way that shows that the law of physics is independent of the choice of coordinates. We can do this in the context of tensor algebra as well. Ironically, this will require us to explicitly work with the coordinate representation, but this work will be augmented by the fact that we require our tensors to transform in specific ways.
In Newtonian mechanics we can look to symmetries and the invariance of the action with respect to those symmetries to express the equations of motion. Our symmetries in Newtonian mechanics leave the action invariant with respect to spatial translation and with respect to rotation.
We want to express relativistic dynamics in a similar way, and will have to express the action as a Lorentz scalar. We are going to impose the symmetries of the Poincare group to determine the relativistic laws of dynamics, and the next task will be to consider the possibilities for our relativistic action, and see what that action implies for dynamics in a relativistic context.
References
[1] L.D. Landau and E.M. Lifshits. The classical theory of fields. Butterworth-Heinemann, 1980.
axis.
as in figure (1). The equation of the ellipse in the rotated coordinates is
and
in the “fixed” frame. Consider figure (2) where our coordinate conventions are illustrated. With
we find
a Jones vector representation of our rotated ellipse
argument, we can write this as
,
, and
. Portions of this problem I tried in Mathematica starting from the elliptic equation derived in section 8.1.3 of [2]. I’d used Mathematica since on paper I found the rotation angle that eliminated the cross terms to always be 45 degrees, but this turns out to have been because I’d first used a change of variables that scaled the equation. Here’s the whole procedure without any such scaling to arrive at the desired result for this problem. Our starting point is the Jones specified field, again as above I’ve using
we have
from
we have
, and 1.2.17 we have
,
and rotating our primed coordinate frame by
degrees



