[Click here for a PDF of this post with nicer formatting (especially if my latex to wordpress script has left FORMULA DOES NOT PARSE errors.)]
Motivation.
I was having algebraic trouble verifying orthonormality relationships for spinor solutions to the Dirac free particle equation, and initially started preparing these notes to post a question to physicsforums. However, in the process of doing so, I spotted my error. A side effect of making these notes is that I got a nice summary of some of the relationships, and it was a good starting point for some personal notes expanding on the content of these chapters.
Context for the original question.
In Desai’s QM book [1], the non-covariant form of the free particle equation is developed as

where each block in the matrix above is two by two. Recall that
\begin{subequations}

\end{subequations}
so

For spin up  and spin down
and spin down  states, the positive energy solutions
states, the positive energy solutions  are found to be
are found to be

and the negative energy states associated with  are found to be
are found to be

The z-axis spin up state  and spin down state
and spin down state  are also used to find one specific set of states for the positive energy solutions
are also used to find one specific set of states for the positive energy solutions
\begin{subequations}

\end{subequations}
and negative energy solutions
\begin{subequations}

\end{subequations}
(the book uses  for both the negative energy states, but I’ve used
for both the negative energy states, but I’ve used  here for the negative states for consistency with the covariant equation solutions).
here for the negative states for consistency with the covariant equation solutions).
Later a complete set of states  are identified as solutions to the covariant Dirac equations
are identified as solutions to the covariant Dirac equations  ,
,  , where
, where  as follows
as follows
\begin{subequations}

\end{subequations}
Note very carefully the sign change above. This is important, since without that we do not have a zero inner product between all  and
and  states. Spelled out explicitly, these states for the z-axis spin up case are
states. Spelled out explicitly, these states for the z-axis spin up case are
\begin{subequations}

\end{subequations}
In order to construct a covariant current conservation relationship a quantity, the Dirac adjoint, was defined as

where

This Dirac adjoint can be used to form an inner product of the form

It’s claimed in the text that we have  ,
,  , and
, and  . Let’s verify all these relationships.
. Let’s verify all these relationships.
Some checks.
Verify the non-covariant solutions.
A non-relativistic approximation argument was used to determine the solutions 2.6a, but we can verify that these hold generally by substitution. For example, for the positive energy z-axis spin up state we have

Here the relationship between the free particle’s energy and momentum  has been used, so we have a zero as desired, and no non-relativistic approximations are required. We can show this generally too, without requiring the specifics of the z-axis spin up or down solutions. This is actually even easier. For the positive energy solutions 2.4 we have
has been used, so we have a zero as desired, and no non-relativistic approximations are required. We can show this generally too, without requiring the specifics of the z-axis spin up or down solutions. This is actually even easier. For the positive energy solutions 2.4 we have

where the identity  has been used. For the negative energy solutions 2.5 we have
has been used. For the negative energy solutions 2.5 we have

Is there something special about the z-axis orientation?
Why was the z-axis spin orientation picked? It doesn’t seem to me that there would be any reason for this. For y-axis spin, recall that our eigenstates are

Our positive energy states should therefore be

It is straightforward to verify that these are solutions. We find for example that

as expected. What’s the general solution? For

we find

with eigenstates
\begin{subequations}

\end{subequations}
Should we wish to consider an arbitrarily oriented spin, expressing 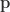 in spherical coordinates also makes sense
in spherical coordinates also makes sense

and we find (with 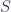 and
and 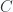 for
for  and
and  respectively)
respectively)
\begin{subequations}

\end{subequations}
Substitution back into 2.4, and 2.5 is then easy. Expressing these with the angles expressed as sums and differences is strongly suggested. With  , and
, and  this gives
this gives
\begin{subequations}

\end{subequations}
This is probably about as tidy as things can be made for the general case.
Expanding the current equation.
With

We can expand the current for a general spin up or spin down state  with respect to either the positive energy or negative energy solutions.
with respect to either the positive energy or negative energy solutions.
Those (normalized) solutions are respectively

For the  th component of the positive energy solution current we have
th component of the positive energy solution current we have

Similarly for a negative energy solution we have

We can expand the inner term of both easily

so that we have for the positive and negative energy solutions currents of

This finds the velocity dependence noted in section 33.4, but does not require taking any specific spin orientation, nor any specific momentum direction.
Unpacking the covariant equation.
Pre-multiplication of the covariant Dirac equation by  should provide a space-time split of the Dirac equation. Let’s verify this
should provide a space-time split of the Dirac equation. Let’s verify this

but


This recovers 2.1 as expected.
Two by two form for the covariant equations.
If we put the covariant Dirac equations in two by two matrix form we get

and

This form makes it easy to verify that our solutions are

and

It’s curious to consider these part of a basis for a single equation. I suppose that all together they are actually eigenstates of the equation

or

which have the form of the Klein-Gordan equation.
Orthonormality.
Orthonormality for the  vectors is easy to show, and we can do so without requiring any specific spin orientation
vectors is easy to show, and we can do so without requiring any specific spin orientation

It’s also easy for  vectors
vectors

For the cross terms we have

Resolution of identity.
It’s claimed that an identity representation is

This makes some sense, but we can see systematically why we have this negative sign. Suppose that we have a basis  for which we have
for which we have  (rather than the strict orthonormality condition
(rather than the strict orthonormality condition  ). Consider the calculation of the Fourier coefficients of a state
). Consider the calculation of the Fourier coefficients of a state

We have

For 
 , so that the coefficient is
, so that the coefficient is

The coordinate representation of this state vector with respect to this basis is thus

Shuffling things around, employing the somewhat abusive seeming Dirac ket-bra operator notation, we find the general identity operation takes the form

so that the identity itself has the form

This is the sum of all the ket-bras for which the braket is one, minus the sum of all the ket-bras for which the braket is negative, showing that the form of the claimed identity is justified.
We can also verify this directly by computation, and find

We can pull the summation into the matrices and note that  (the two by two identity), so that we are left with
(the two by two identity), so that we are left with

Similarly, we find

summing the two (noting that  ) we get the block identity matrix as desired.
) we get the block identity matrix as desired.
We’ve also just calculated the projection operators. Let’s verify that expanding the covariant form in the text produces the same result

Now compare to 3.39, and 3.40, which we rewrite using  as
as

Lorentz transformation of Dirac equation.
Equation (35.107) in the text is missing the positional notation to show the placement of the indexes, and should be
![\begin{aligned}\left[{\Sigma},{\gamma^\nu}\right] = e_\mu^{.\nu} \gamma^\mu,\end{aligned} \hspace{\stretch{1}}(3.45)](https://s0.wp.com/latex.php?latex=%5Cbegin%7Baligned%7D%5Cleft%5B%7B%5CSigma%7D%2C%7B%5Cgamma%5E%5Cnu%7D%5Cright%5D+%3D+e_%5Cmu%5E%7B.%5Cnu%7D+%5Cgamma%5E%5Cmu%2C%5Cend%7Baligned%7D+%5Chspace%7B%5Cstretch%7B1%7D%7D%283.45%29&bg=fafcff&fg=2a2a2a&s=0&c=20201002)
where the solution is

This does have the form I’d expect, a bivector, but we can show explicitly that this is the solution without too much trouble. Consider the commutator
![\begin{aligned}\left[{ \gamma^\alpha \gamma^\beta e_{\alpha \beta} },{\gamma^\nu}\right]&=e_{\alpha \beta} \left[{ \gamma^\alpha \gamma^\beta },{\gamma^\nu}\right] \\ &=e_{\alpha \beta} \left( \gamma^\alpha \gamma^\beta \gamma^\nu-\gamma^\nu \gamma^\alpha \gamma^\beta \right) \\ &=e_{\alpha \beta} \left( \left( {\gamma^\alpha \cdot \gamma^\beta }+\gamma^\alpha \wedge \gamma^\beta \right) \gamma^\nu-\gamma^\nu \left( {\gamma^\alpha \cdot \gamma^\beta }+\gamma^\alpha \wedge \gamma^\beta \right) \right) \\ &=e_{\alpha \beta} \left(\left(\gamma^\alpha \wedge \gamma^\beta \right)\gamma^\nu-\gamma^\nu \left(\gamma^\alpha \wedge \gamma^\beta \right)\right)\\ &=e_{\alpha \beta} \left(\left(\gamma^\alpha \wedge \gamma^\beta \right) \wedge \gamma^\nu-\gamma^\nu \wedge \left(\gamma^\alpha \wedge \gamma^\beta \right)\right)+e_{\alpha \beta} \left(\left(\gamma^\alpha \wedge \gamma^\beta \right) \cdot \gamma^\nu-\gamma^\nu \cdot \left(\gamma^\alpha \wedge \gamma^\beta \right)\right)\\ &=2 e_{\alpha \beta} \left(\gamma^\alpha \wedge \gamma^\beta \right) \cdot \gamma^\nu\\ &=2 e^{\alpha \beta} \left(\gamma_\alpha \wedge \gamma_\beta \right) \cdot \gamma^\nu\\ &=2 e^{\alpha \beta} \left(\gamma_\alpha \delta_\beta^{.\nu}-\gamma_\beta \delta_\alpha^{.\nu}\right)\\ &=4 e^{\alpha \nu} \gamma_\alpha \\ &=4 e_\alpha^{.\nu} \gamma^\alpha \\ \end{aligned}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Baligned%7D%5Cleft%5B%7B+%5Cgamma%5E%5Calpha+%5Cgamma%5E%5Cbeta+e_%7B%5Calpha+%5Cbeta%7D+%7D%2C%7B%5Cgamma%5E%5Cnu%7D%5Cright%5D%26%3De_%7B%5Calpha+%5Cbeta%7D+%5Cleft%5B%7B+%5Cgamma%5E%5Calpha+%5Cgamma%5E%5Cbeta+%7D%2C%7B%5Cgamma%5E%5Cnu%7D%5Cright%5D+%5C%5C+%26%3De_%7B%5Calpha+%5Cbeta%7D+%5Cleft%28+%5Cgamma%5E%5Calpha+%5Cgamma%5E%5Cbeta+%5Cgamma%5E%5Cnu-%5Cgamma%5E%5Cnu+%5Cgamma%5E%5Calpha+%5Cgamma%5E%5Cbeta+%5Cright%29+%5C%5C+%26%3De_%7B%5Calpha+%5Cbeta%7D+%5Cleft%28+%5Cleft%28+%7B%5Cgamma%5E%5Calpha+%5Ccdot+%5Cgamma%5E%5Cbeta+%7D%2B%5Cgamma%5E%5Calpha+%5Cwedge+%5Cgamma%5E%5Cbeta+%5Cright%29+%5Cgamma%5E%5Cnu-%5Cgamma%5E%5Cnu+%5Cleft%28+%7B%5Cgamma%5E%5Calpha+%5Ccdot+%5Cgamma%5E%5Cbeta+%7D%2B%5Cgamma%5E%5Calpha+%5Cwedge+%5Cgamma%5E%5Cbeta+%5Cright%29+%5Cright%29+%5C%5C+%26%3De_%7B%5Calpha+%5Cbeta%7D+%5Cleft%28%5Cleft%28%5Cgamma%5E%5Calpha+%5Cwedge+%5Cgamma%5E%5Cbeta+%5Cright%29%5Cgamma%5E%5Cnu-%5Cgamma%5E%5Cnu+%5Cleft%28%5Cgamma%5E%5Calpha+%5Cwedge+%5Cgamma%5E%5Cbeta+%5Cright%29%5Cright%29%5C%5C+%26%3De_%7B%5Calpha+%5Cbeta%7D+%5Cleft%28%5Cleft%28%5Cgamma%5E%5Calpha+%5Cwedge+%5Cgamma%5E%5Cbeta+%5Cright%29+%5Cwedge+%5Cgamma%5E%5Cnu-%5Cgamma%5E%5Cnu+%5Cwedge+%5Cleft%28%5Cgamma%5E%5Calpha+%5Cwedge+%5Cgamma%5E%5Cbeta+%5Cright%29%5Cright%29%2Be_%7B%5Calpha+%5Cbeta%7D+%5Cleft%28%5Cleft%28%5Cgamma%5E%5Calpha+%5Cwedge+%5Cgamma%5E%5Cbeta+%5Cright%29+%5Ccdot+%5Cgamma%5E%5Cnu-%5Cgamma%5E%5Cnu+%5Ccdot+%5Cleft%28%5Cgamma%5E%5Calpha+%5Cwedge+%5Cgamma%5E%5Cbeta+%5Cright%29%5Cright%29%5C%5C+%26%3D2+e_%7B%5Calpha+%5Cbeta%7D+%5Cleft%28%5Cgamma%5E%5Calpha+%5Cwedge+%5Cgamma%5E%5Cbeta+%5Cright%29+%5Ccdot+%5Cgamma%5E%5Cnu%5C%5C+%26%3D2+e%5E%7B%5Calpha+%5Cbeta%7D+%5Cleft%28%5Cgamma_%5Calpha+%5Cwedge+%5Cgamma_%5Cbeta+%5Cright%29+%5Ccdot+%5Cgamma%5E%5Cnu%5C%5C+%26%3D2+e%5E%7B%5Calpha+%5Cbeta%7D+%5Cleft%28%5Cgamma_%5Calpha+%5Cdelta_%5Cbeta%5E%7B.%5Cnu%7D-%5Cgamma_%5Cbeta++%5Cdelta_%5Calpha%5E%7B.%5Cnu%7D%5Cright%29%5C%5C+%26%3D4+e%5E%7B%5Calpha+%5Cnu%7D+%5Cgamma_%5Calpha+%5C%5C+%26%3D4+e_%5Calpha%5E%7B.%5Cnu%7D+%5Cgamma%5E%5Calpha+%5C%5C+%5Cend%7Baligned%7D+&bg=fafcff&fg=2a2a2a&s=0&c=20201002)
Would this be any easier to prove without utilizing the dot and wedge product identities? I used a few of them, starting with
![\begin{aligned}a \cdot b &= \frac{1}{{2}} (a b + b a) = \frac{1}{{2}} \left\{{a},{b}\right\} \\ a \wedge b &= \frac{1}{{2}} (a b - b a) = \frac{1}{{2}} \left[{a},{b}\right] \\ a b &= a \cdot b + a \wedge b = \frac{1}{{2}} ( \left\{{a},{b}\right\} + \left[{a},{b}\right] )\end{aligned} \hspace{\stretch{1}}(3.45)](https://s0.wp.com/latex.php?latex=%5Cbegin%7Baligned%7Da+%5Ccdot+b+%26%3D+%5Cfrac%7B1%7D%7B%7B2%7D%7D+%28a+b+%2B+b+a%29+%3D+%5Cfrac%7B1%7D%7B%7B2%7D%7D+%5Cleft%5C%7B%7Ba%7D%2C%7Bb%7D%5Cright%5C%7D+%5C%5C+a+%5Cwedge+b+%26%3D+%5Cfrac%7B1%7D%7B%7B2%7D%7D+%28a+b+-+b+a%29+%3D+%5Cfrac%7B1%7D%7B%7B2%7D%7D+%5Cleft%5B%7Ba%7D%2C%7Bb%7D%5Cright%5D+%5C%5C+a+b+%26%3D+a+%5Ccdot+b+%2B+a+%5Cwedge+b+%3D+%5Cfrac%7B1%7D%7B%7B2%7D%7D+%28+%5Cleft%5C%7B%7Ba%7D%2C%7Bb%7D%5Cright%5C%7D+%2B+%5Cleft%5B%7Ba%7D%2C%7Bb%7D%5Cright%5D+%29%5Cend%7Baligned%7D+%5Chspace%7B%5Cstretch%7B1%7D%7D%283.45%29&bg=fafcff&fg=2a2a2a&s=0&c=20201002)
In matrix notation we would have to show that the anticommutator  commutes with any
commutes with any  to make the first cancellation. We can do so by noting
to make the first cancellation. We can do so by noting
![\begin{aligned}\left[{\gamma^\alpha \gamma^\beta + \gamma^\beta \gamma^\alpha},{\gamma^\nu}\right] &= \left[{ 2 g^{\alpha \beta} \mathbf{1}},{\gamma^\nu}\right] \\ &= 2 g^{\alpha \beta} \left[{\mathbf{1}},{\gamma^\nu}\right] \\ &= 0\end{aligned}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Baligned%7D%5Cleft%5B%7B%5Cgamma%5E%5Calpha+%5Cgamma%5E%5Cbeta+%2B+%5Cgamma%5E%5Cbeta+%5Cgamma%5E%5Calpha%7D%2C%7B%5Cgamma%5E%5Cnu%7D%5Cright%5D+%26%3D+%5Cleft%5B%7B+2+g%5E%7B%5Calpha+%5Cbeta%7D+%5Cmathbf%7B1%7D%7D%2C%7B%5Cgamma%5E%5Cnu%7D%5Cright%5D+%5C%5C+%26%3D+2+g%5E%7B%5Calpha+%5Cbeta%7D+%5Cleft%5B%7B%5Cmathbf%7B1%7D%7D%2C%7B%5Cgamma%5E%5Cnu%7D%5Cright%5D+%5C%5C+%26%3D+0%5Cend%7Baligned%7D+&bg=fafcff&fg=2a2a2a&s=0&c=20201002)
That’s enough to get us on the path to how to prove this in matrix form
![\begin{aligned}\left[{ \gamma^\alpha \gamma^\beta e_{\alpha \beta} },{\gamma^\nu}\right]&=e_{\alpha \beta} \left[{ \gamma^\alpha \gamma^\beta },{\gamma^\nu}\right] \\ &=e_{\alpha \beta} \left( \gamma^\alpha \gamma^\beta \gamma^\nu-\gamma^\nu \gamma^\alpha \gamma^\beta \right) \\ &=\frac{1}{{2}} e_{\alpha \beta} \left( \left( \left\{{\gamma^\alpha},{\gamma^\beta}\right\}+\left[{\gamma^\alpha },{ \gamma^\beta }\right]\right) \gamma^\nu-\gamma^\nu \left( \left\{{\gamma^\alpha },{\gamma^\beta }\right\}+\left[{\gamma^\alpha },{\gamma^\beta }\right]\right) \right) \\ &=\frac{1}{{2}} e_{\alpha \beta} \left( \left[{\gamma^\alpha },{ \gamma^\beta }\right] \gamma^\nu-\gamma^\nu \left[{\gamma^\alpha },{ \gamma^\beta }\right] \right) \\ &=\frac{1}{{2}} e_{\alpha \beta} \left[{\left[{\gamma^\alpha },{ \gamma^\beta }\right] },{\gamma^\nu}\right] \\ &=\frac{1}{{2}} e_{\alpha \beta} \left[{\left[{\gamma^\alpha },{ \gamma^\beta }\right] },{\gamma^\nu}\right] \\ &=\frac{1}{{2}} e_{\alpha \beta} \left[{\gamma^\alpha \gamma^\beta -\gamma^\beta \gamma^\alpha },{\gamma^\nu}\right] \\ &=e_{\alpha \beta} \left[{\gamma^\alpha \gamma^\beta },{\gamma^\nu}\right] \\ &=e_{\alpha \beta} \left(\gamma^\alpha \gamma^\beta \gamma^\nu-\gamma^\nu \gamma^\alpha \gamma^\beta \right) \\ &=e_{\alpha \beta} \left(\gamma^\alpha ( 2 g^{\beta \nu} - \gamma^\nu \gamma^\beta )-\gamma^\nu \gamma^\alpha \gamma^\beta \right) \\ &=e_{\alpha \beta} \left(2 \gamma^\alpha g^{\beta \nu} - \gamma^\alpha \gamma^\nu \gamma^\beta -\gamma^\nu \gamma^\alpha \gamma^\beta \right) \\ &=2 e_{\alpha \beta} \left(\gamma^\alpha g^{\beta \nu} - g^{\alpha \nu} \gamma^\beta \right) \\ &=2 e_{\alpha \beta} \gamma^\alpha g^{\beta \nu} + 2 e_{\beta \alpha} g^{\alpha \nu} \gamma^\beta \\ &=2 e_{\alpha}^{. \nu} \gamma^\alpha + 2 e_{\beta}^{.\nu} \gamma^\beta \\ &=4 e_{\alpha}^{. \nu} \gamma^\alpha \end{aligned}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Baligned%7D%5Cleft%5B%7B+%5Cgamma%5E%5Calpha+%5Cgamma%5E%5Cbeta+e_%7B%5Calpha+%5Cbeta%7D+%7D%2C%7B%5Cgamma%5E%5Cnu%7D%5Cright%5D%26%3De_%7B%5Calpha+%5Cbeta%7D+%5Cleft%5B%7B+%5Cgamma%5E%5Calpha+%5Cgamma%5E%5Cbeta+%7D%2C%7B%5Cgamma%5E%5Cnu%7D%5Cright%5D+%5C%5C+%26%3De_%7B%5Calpha+%5Cbeta%7D+%5Cleft%28+%5Cgamma%5E%5Calpha+%5Cgamma%5E%5Cbeta+%5Cgamma%5E%5Cnu-%5Cgamma%5E%5Cnu+%5Cgamma%5E%5Calpha+%5Cgamma%5E%5Cbeta+%5Cright%29+%5C%5C+%26%3D%5Cfrac%7B1%7D%7B%7B2%7D%7D+e_%7B%5Calpha+%5Cbeta%7D+%5Cleft%28+%5Cleft%28+%5Cleft%5C%7B%7B%5Cgamma%5E%5Calpha%7D%2C%7B%5Cgamma%5E%5Cbeta%7D%5Cright%5C%7D%2B%5Cleft%5B%7B%5Cgamma%5E%5Calpha+%7D%2C%7B+%5Cgamma%5E%5Cbeta+%7D%5Cright%5D%5Cright%29+%5Cgamma%5E%5Cnu-%5Cgamma%5E%5Cnu+%5Cleft%28+%5Cleft%5C%7B%7B%5Cgamma%5E%5Calpha+%7D%2C%7B%5Cgamma%5E%5Cbeta+%7D%5Cright%5C%7D%2B%5Cleft%5B%7B%5Cgamma%5E%5Calpha+%7D%2C%7B%5Cgamma%5E%5Cbeta+%7D%5Cright%5D%5Cright%29+%5Cright%29+%5C%5C+%26%3D%5Cfrac%7B1%7D%7B%7B2%7D%7D+e_%7B%5Calpha+%5Cbeta%7D+%5Cleft%28+%5Cleft%5B%7B%5Cgamma%5E%5Calpha+%7D%2C%7B+%5Cgamma%5E%5Cbeta+%7D%5Cright%5D+%5Cgamma%5E%5Cnu-%5Cgamma%5E%5Cnu+%5Cleft%5B%7B%5Cgamma%5E%5Calpha+%7D%2C%7B+%5Cgamma%5E%5Cbeta+%7D%5Cright%5D+%5Cright%29+%5C%5C+%26%3D%5Cfrac%7B1%7D%7B%7B2%7D%7D+e_%7B%5Calpha+%5Cbeta%7D+%5Cleft%5B%7B%5Cleft%5B%7B%5Cgamma%5E%5Calpha+%7D%2C%7B+%5Cgamma%5E%5Cbeta+%7D%5Cright%5D+%7D%2C%7B%5Cgamma%5E%5Cnu%7D%5Cright%5D+%5C%5C+%26%3D%5Cfrac%7B1%7D%7B%7B2%7D%7D+e_%7B%5Calpha+%5Cbeta%7D+%5Cleft%5B%7B%5Cleft%5B%7B%5Cgamma%5E%5Calpha+%7D%2C%7B+%5Cgamma%5E%5Cbeta+%7D%5Cright%5D+%7D%2C%7B%5Cgamma%5E%5Cnu%7D%5Cright%5D+%5C%5C+%26%3D%5Cfrac%7B1%7D%7B%7B2%7D%7D+e_%7B%5Calpha+%5Cbeta%7D+%5Cleft%5B%7B%5Cgamma%5E%5Calpha+%5Cgamma%5E%5Cbeta+-%5Cgamma%5E%5Cbeta+%5Cgamma%5E%5Calpha+%7D%2C%7B%5Cgamma%5E%5Cnu%7D%5Cright%5D+%5C%5C+%26%3De_%7B%5Calpha+%5Cbeta%7D+%5Cleft%5B%7B%5Cgamma%5E%5Calpha+%5Cgamma%5E%5Cbeta+%7D%2C%7B%5Cgamma%5E%5Cnu%7D%5Cright%5D+%5C%5C+%26%3De_%7B%5Calpha+%5Cbeta%7D+%5Cleft%28%5Cgamma%5E%5Calpha+%5Cgamma%5E%5Cbeta+%5Cgamma%5E%5Cnu-%5Cgamma%5E%5Cnu+%5Cgamma%5E%5Calpha+%5Cgamma%5E%5Cbeta+%5Cright%29+%5C%5C+%26%3De_%7B%5Calpha+%5Cbeta%7D+%5Cleft%28%5Cgamma%5E%5Calpha+%28+2+g%5E%7B%5Cbeta+%5Cnu%7D+-+%5Cgamma%5E%5Cnu+%5Cgamma%5E%5Cbeta+%29-%5Cgamma%5E%5Cnu+%5Cgamma%5E%5Calpha+%5Cgamma%5E%5Cbeta+%5Cright%29+%5C%5C+%26%3De_%7B%5Calpha+%5Cbeta%7D+%5Cleft%282+%5Cgamma%5E%5Calpha+g%5E%7B%5Cbeta+%5Cnu%7D+-+%5Cgamma%5E%5Calpha+%5Cgamma%5E%5Cnu+%5Cgamma%5E%5Cbeta+-%5Cgamma%5E%5Cnu+%5Cgamma%5E%5Calpha+%5Cgamma%5E%5Cbeta+%5Cright%29+%5C%5C+%26%3D2+e_%7B%5Calpha+%5Cbeta%7D+%5Cleft%28%5Cgamma%5E%5Calpha+g%5E%7B%5Cbeta+%5Cnu%7D+-+g%5E%7B%5Calpha+%5Cnu%7D+%5Cgamma%5E%5Cbeta+%5Cright%29+%5C%5C+%26%3D2+e_%7B%5Calpha+%5Cbeta%7D+%5Cgamma%5E%5Calpha+g%5E%7B%5Cbeta+%5Cnu%7D+%2B+2+e_%7B%5Cbeta+%5Calpha%7D+g%5E%7B%5Calpha+%5Cnu%7D+%5Cgamma%5E%5Cbeta++%5C%5C+%26%3D2+e_%7B%5Calpha%7D%5E%7B.+%5Cnu%7D+%5Cgamma%5E%5Calpha+%2B+2+e_%7B%5Cbeta%7D%5E%7B.%5Cnu%7D+%5Cgamma%5E%5Cbeta++%5C%5C+%26%3D4+e_%7B%5Calpha%7D%5E%7B.+%5Cnu%7D+%5Cgamma%5E%5Calpha+%5Cend%7Baligned%7D+&bg=fafcff&fg=2a2a2a&s=0&c=20201002)
References
[1] BR Desai. Quantum mechanics with basic field theory. Cambridge University Press, 2009.