[Click here for a PDF of this post with nicer formatting]
Disclaimer.
This problem set is as yet ungraded (although only the second question will be graded).
Problem 1. Fun with  ,
,  ,
,  , and the duality of Maxwell’s equations in vacuum.
, and the duality of Maxwell’s equations in vacuum.
1. Statement. rank 3 spatial antisymmetric tensor identities.
Prove that

and use it to find the familiar relation for

Also show that

(Einstein summation implied all throughout this problem).
1. Solution
We can explicitly expand the (implied) sum over indexes  . This is
. This is

For any  only one term is non-zero. For example with
only one term is non-zero. For example with  , we have just a contribution from the
, we have just a contribution from the  part of the sum
part of the sum

The value of this for  is
is

whereas for  we have
we have

Our sum has value one when  matches
matches  , and value minus one for when
, and value minus one for when  are permuted. We can summarize this, by saying that when
are permuted. We can summarize this, by saying that when  we have
we have

However, observe that when  the RHS is
the RHS is

as desired, so this form works in general without any  qualifier, completing this part of the problem.
qualifier, completing this part of the problem.

This gives us

We have one more identity to deal with.

We can expand out this (implied) sum slow and dumb as well

Now, observe that for any  only one term of this sum is picked up. For example, with no loss of generality, pick
only one term of this sum is picked up. For example, with no loss of generality, pick  . We are left with only
. We are left with only

This has the value

when  and is zero otherwise. We can therefore summarize the evaluation of this sum as
and is zero otherwise. We can therefore summarize the evaluation of this sum as

completing this problem.
2. Statement. Determinant of three by three matrix.
Prove that for any  matrix
matrix  :
:  and that
and that  .
.
2. Solution
In class Simon showed us how the first identity can be arrived at using the triple product  . It occurred to me later that I’d seen the identity to be proven in the context of Geometric Algebra, but hadn’t recognized it in this tensor form. Basically, a wedge product can be expanded in sums of determinants, and when the dimension of the space is the same as the vector, we have a pseudoscalar times the determinant of the components.
. It occurred to me later that I’d seen the identity to be proven in the context of Geometric Algebra, but hadn’t recognized it in this tensor form. Basically, a wedge product can be expanded in sums of determinants, and when the dimension of the space is the same as the vector, we have a pseudoscalar times the determinant of the components.
For example, in 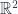 , let’s take the wedge product of a pair of vectors. As preparation for the relativistic
, let’s take the wedge product of a pair of vectors. As preparation for the relativistic 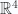 case We won’t require an orthonormal basis, but express the vector in terms of a reciprocal frame and the associated components
case We won’t require an orthonormal basis, but express the vector in terms of a reciprocal frame and the associated components

where

When we get to the relativistic case, we can pick (but don’t have to) the standard basis

for which our reciprocal frame is implicitly defined by the metric

Anyways. Back to the problem. Let’s examine the 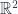 case. Our wedge product in coordinates is
case. Our wedge product in coordinates is

Since there are only two basis vectors we have

Our wedge product is a product of the determinant of the vector coordinates, times the 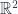 pseudoscalar
pseudoscalar  .
.
This doesn’t look quite like the 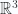 relation that we want to prove, which had an antisymmetric tensor factor for the determinant. Observe that we get the determinant by picking off the
relation that we want to prove, which had an antisymmetric tensor factor for the determinant. Observe that we get the determinant by picking off the  component of the bivector result (the only component in this case), and we can do that by dotting with
component of the bivector result (the only component in this case), and we can do that by dotting with  . To get an antisymmetric tensor times the determinant, we have only to dot with a different pseudoscalar (one that differs by a possible sign due to permutation of the indexes). That is
. To get an antisymmetric tensor times the determinant, we have only to dot with a different pseudoscalar (one that differs by a possible sign due to permutation of the indexes). That is
![\begin{aligned}(e^t \wedge e^s) \cdot (a \wedge b)&=a^i b^j (e^t \wedge e^s) \cdot (e_i \wedge e_j) \\ &=a^i b^j\left( {\delta^{s}}_i {\delta^{t}}_j-{\delta^{t}}_i {\delta^{s}}_j \right) \\ &=a^i b^j{\delta^{[t}}_j {\delta^{s]}}_i \\ &=a^i b^j{\delta^{t}}_{[j} {\delta^{s}}_{i]} \\ &=a^{[i} b^{j]}{\delta^{t}}_{j} {\delta^{s}}_{i} \\ &=a^{[s} b^{t]}\end{aligned}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Baligned%7D%28e%5Et+%5Cwedge+e%5Es%29+%5Ccdot+%28a+%5Cwedge+b%29%26%3Da%5Ei+b%5Ej+%28e%5Et+%5Cwedge+e%5Es%29+%5Ccdot+%28e_i+%5Cwedge+e_j%29+%5C%5C+%26%3Da%5Ei+b%5Ej%5Cleft%28+%7B%5Cdelta%5E%7Bs%7D%7D_i+%7B%5Cdelta%5E%7Bt%7D%7D_j-%7B%5Cdelta%5E%7Bt%7D%7D_i+%7B%5Cdelta%5E%7Bs%7D%7D_j++%5Cright%29+%5C%5C+%26%3Da%5Ei+b%5Ej%7B%5Cdelta%5E%7B%5Bt%7D%7D_j+%7B%5Cdelta%5E%7Bs%5D%7D%7D_i+%5C%5C+%26%3Da%5Ei+b%5Ej%7B%5Cdelta%5E%7Bt%7D%7D_%7B%5Bj%7D+%7B%5Cdelta%5E%7Bs%7D%7D_%7Bi%5D%7D+%5C%5C+%26%3Da%5E%7B%5Bi%7D+b%5E%7Bj%5D%7D%7B%5Cdelta%5E%7Bt%7D%7D_%7Bj%7D+%7B%5Cdelta%5E%7Bs%7D%7D_%7Bi%7D+%5C%5C+%26%3Da%5E%7B%5Bs%7D+b%5E%7Bt%5D%7D%5Cend%7Baligned%7D+&bg=fafcff&fg=2a2a2a&s=0&c=20201002)
Now, if we write  and
and  we have
we have

We can write this in two different ways. One of which is

and the other of which is by introducing free indexes for  and
and  , and summing antisymmetrically over these. That is
, and summing antisymmetrically over these. That is

So, we have
![\begin{aligned}\boxed{A^{a s} A^{b t} \epsilon_{a b} =A^{1 i} A^{2 j} {\delta^{[t}}_j {\delta^{s]}}_i =\epsilon^{s t} \text{Det} {\left\lVert{A^{ij}}\right\rVert},}\end{aligned} \hspace{\stretch{1}}(2.30)](https://s0.wp.com/latex.php?latex=%5Cbegin%7Baligned%7D%5Cboxed%7BA%5E%7Ba+s%7D+A%5E%7Bb+t%7D+%5Cepsilon_%7Ba+b%7D+%3DA%5E%7B1+i%7D+A%5E%7B2+j%7D+%7B%5Cdelta%5E%7B%5Bt%7D%7D_j+%7B%5Cdelta%5E%7Bs%5D%7D%7D_i+%3D%5Cepsilon%5E%7Bs+t%7D+%5Ctext%7BDet%7D+%7B%5Cleft%5ClVert%7BA%5E%7Bij%7D%7D%5Cright%5CrVert%7D%2C%7D%5Cend%7Baligned%7D+%5Chspace%7B%5Cstretch%7B1%7D%7D%282.30%29&bg=fafcff&fg=2a2a2a&s=0&c=20201002)
This result hold regardless of the metric for the space, and does not require that we were using an orthonormal basis. When the metric is Euclidean and we have an orthonormal basis, then all the indexes can be dropped.
The 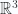 and
and 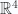 cases follow in exactly the same way, we just need more vectors in the wedge products.
cases follow in exactly the same way, we just need more vectors in the wedge products.
For the 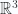 case we have
case we have
![\begin{aligned}(e^u \wedge e^t \wedge e^s) \cdot ( a \wedge b \wedge c)&=a^i b^j c^k(e^u \wedge e^t \wedge e^s) \cdot (e_i \wedge e_j \wedge e_k) \\ &=a^i b^j c^k{\delta^{[u}}_k{\delta^{t}}_j{\delta^{s]}}_i \\ &=a^{[s} b^t c^{u]}\end{aligned}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Baligned%7D%28e%5Eu+%5Cwedge+e%5Et+%5Cwedge+e%5Es%29+%5Ccdot+%28+a+%5Cwedge+b+%5Cwedge+c%29%26%3Da%5Ei+b%5Ej+c%5Ek%28e%5Eu+%5Cwedge+e%5Et+%5Cwedge+e%5Es%29+%5Ccdot+%28e_i+%5Cwedge+e_j+%5Cwedge+e_k%29+%5C%5C+%26%3Da%5Ei+b%5Ej+c%5Ek%7B%5Cdelta%5E%7B%5Bu%7D%7D_k%7B%5Cdelta%5E%7Bt%7D%7D_j%7B%5Cdelta%5E%7Bs%5D%7D%7D_i+%5C%5C+%26%3Da%5E%7B%5Bs%7D+b%5Et+c%5E%7Bu%5D%7D%5Cend%7Baligned%7D+&bg=fafcff&fg=2a2a2a&s=0&c=20201002)
Again, with  and
and  , and
, and  we have
we have
![\begin{aligned}(e^u \wedge e^t \wedge e^s) \cdot ( a \wedge b \wedge c)=A^{1 i} A^{2 j} A^{3 k}{\delta^{[u}}_k{\delta^{t}}_j{\delta^{s]}}_i\end{aligned} \hspace{\stretch{1}}(2.31)](https://s0.wp.com/latex.php?latex=%5Cbegin%7Baligned%7D%28e%5Eu+%5Cwedge+e%5Et+%5Cwedge+e%5Es%29+%5Ccdot+%28+a+%5Cwedge+b+%5Cwedge+c%29%3DA%5E%7B1+i%7D+A%5E%7B2+j%7D+A%5E%7B3+k%7D%7B%5Cdelta%5E%7B%5Bu%7D%7D_k%7B%5Cdelta%5E%7Bt%7D%7D_j%7B%5Cdelta%5E%7Bs%5D%7D%7D_i%5Cend%7Baligned%7D+%5Chspace%7B%5Cstretch%7B1%7D%7D%282.31%29&bg=fafcff&fg=2a2a2a&s=0&c=20201002)
and we can choose to write this in either form, resulting in the identity
![\begin{aligned}\boxed{\epsilon^{s t u} \text{Det} {\left\lVert{A^{ij}}\right\rVert}=A^{1 i} A^{2 j} A^{3 k}{\delta^{[u}}_k{\delta^{t}}_j{\delta^{s]}}_i=\epsilon_{a b c} A^{a s} A^{b t} A^{c u}.}\end{aligned} \hspace{\stretch{1}}(2.32)](https://s0.wp.com/latex.php?latex=%5Cbegin%7Baligned%7D%5Cboxed%7B%5Cepsilon%5E%7Bs+t+u%7D+%5Ctext%7BDet%7D+%7B%5Cleft%5ClVert%7BA%5E%7Bij%7D%7D%5Cright%5CrVert%7D%3DA%5E%7B1+i%7D+A%5E%7B2+j%7D+A%5E%7B3+k%7D%7B%5Cdelta%5E%7B%5Bu%7D%7D_k%7B%5Cdelta%5E%7Bt%7D%7D_j%7B%5Cdelta%5E%7Bs%5D%7D%7D_i%3D%5Cepsilon_%7Ba+b+c%7D+A%5E%7Ba+s%7D+A%5E%7Bb+t%7D+A%5E%7Bc+u%7D.%7D%5Cend%7Baligned%7D+%5Chspace%7B%5Cstretch%7B1%7D%7D%282.32%29&bg=fafcff&fg=2a2a2a&s=0&c=20201002)
The 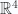 case follows exactly the same way, and we have
case follows exactly the same way, and we have
![\begin{aligned}(e^v \wedge e^u \wedge e^t \wedge e^s) \cdot ( a \wedge b \wedge c \wedge d)&=a^i b^j c^k d^l(e^v \wedge e^u \wedge e^t \wedge e^s) \cdot (e_i \wedge e_j \wedge e_k \wedge e_l) \\ &=a^i b^j c^k d^l{\delta^{[v}}_l{\delta^{u}}_k{\delta^{t}}_j{\delta^{s]}}_i \\ &=a^{[s} b^t c^{u} d^{v]}.\end{aligned}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Baligned%7D%28e%5Ev+%5Cwedge+e%5Eu+%5Cwedge+e%5Et+%5Cwedge+e%5Es%29+%5Ccdot+%28+a+%5Cwedge+b+%5Cwedge+c+%5Cwedge+d%29%26%3Da%5Ei+b%5Ej+c%5Ek+d%5El%28e%5Ev+%5Cwedge+e%5Eu+%5Cwedge+e%5Et+%5Cwedge+e%5Es%29+%5Ccdot+%28e_i+%5Cwedge+e_j+%5Cwedge+e_k+%5Cwedge+e_l%29+%5C%5C+%26%3Da%5Ei+b%5Ej+c%5Ek+d%5El%7B%5Cdelta%5E%7B%5Bv%7D%7D_l%7B%5Cdelta%5E%7Bu%7D%7D_k%7B%5Cdelta%5E%7Bt%7D%7D_j%7B%5Cdelta%5E%7Bs%5D%7D%7D_i+%5C%5C+%26%3Da%5E%7B%5Bs%7D+b%5Et+c%5E%7Bu%7D+d%5E%7Bv%5D%7D.%5Cend%7Baligned%7D+&bg=fafcff&fg=2a2a2a&s=0&c=20201002)
This time with  and
and  , and
, and  , and
, and  we have
we have
![\begin{aligned}\boxed{\epsilon^{s t u v} \text{Det} {\left\lVert{A^{ij}}\right\rVert}=A^{0 i} A^{1 j} A^{2 k} A^{3 l}{\delta^{[v}}_l{\delta^{u}}_k{\delta^{t}}_j{\delta^{s]}}_i=\epsilon_{a b c d} A^{a s} A^{b t} A^{c u} A^{d v}.}\end{aligned} \hspace{\stretch{1}}(2.33)](https://s0.wp.com/latex.php?latex=%5Cbegin%7Baligned%7D%5Cboxed%7B%5Cepsilon%5E%7Bs+t+u+v%7D+%5Ctext%7BDet%7D+%7B%5Cleft%5ClVert%7BA%5E%7Bij%7D%7D%5Cright%5CrVert%7D%3DA%5E%7B0+i%7D+A%5E%7B1+j%7D+A%5E%7B2+k%7D+A%5E%7B3+l%7D%7B%5Cdelta%5E%7B%5Bv%7D%7D_l%7B%5Cdelta%5E%7Bu%7D%7D_k%7B%5Cdelta%5E%7Bt%7D%7D_j%7B%5Cdelta%5E%7Bs%5D%7D%7D_i%3D%5Cepsilon_%7Ba+b+c+d%7D+A%5E%7Ba+s%7D+A%5E%7Bb+t%7D+A%5E%7Bc+u%7D+A%5E%7Bd+v%7D.%7D%5Cend%7Baligned%7D+%5Chspace%7B%5Cstretch%7B1%7D%7D%282.33%29&bg=fafcff&fg=2a2a2a&s=0&c=20201002)
This one is almost the identity to be established later in problem 1.4. We have only to raise and lower some indexes to get that one. Note that in the Minkowski standard basis above, because  must be a permutation of
must be a permutation of  for a non-zero result, we must have
for a non-zero result, we must have

So raising and lowering the identity above gives us

No sign changes were required for the indexes  , since they are paired.
, since they are paired.
Until we did the raising and lowering operations here, there was no specific metric required, so our first result 2.33 is the more general one.
There’s one more part to this problem, doing the antisymmetric sums over the indexes  . For the
. For the 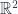 case we have
case we have

We conclude that

For the 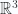 case we have the same operation
case we have the same operation

So we conclude

It’s clear what the pattern is, and if we evaluate the sum of the antisymmetric tensor squares in 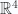 we have
we have

So, for our SR case we have

This was part of question 1.4, albeit in lower index form. Here since all indexes are matched, we have the same result without major change

The main difference is that we are now taking the determinant of a lower index tensor.
3. Statement. Rotational invariance of 3D antisymmetric tensor
Use the previous results to show that  is invariant under rotations.
is invariant under rotations.
3. Solution
We apply transformations to coordinates (and thus indexes) of the form

With our tensor transforming as its indexes, we have

We’ve got 2.32, which after dropping indexes, because we are in a Euclidean space, we have

Let  , which gives us
, which gives us

but since  , we have shown that
, we have shown that  is invariant under rotation.
is invariant under rotation.
4. Statement. Rotational invariance of 4D antisymmetric tensor
Use the previous results to show that  is invariant under Lorentz transformations.
is invariant under Lorentz transformations.
4. Solution
This follows the same way. We assume a transformation of coordinates of the following form

where the determinant of  (sanity check of sign:
(sanity check of sign:  ).
).
Our antisymmetric tensor transforms as its coordinates individually

Let  , and raise and lower all the indexes in 2.46 for
, and raise and lower all the indexes in 2.46 for

We have

Since  both are therefore invariant under Lorentz transformation.
both are therefore invariant under Lorentz transformation.
5. Statement. Sum of contracting symmetric and antisymmetric rank 2 tensors
Show that  if
if  is symmetric and
is symmetric and 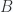 is antisymmetric.
is antisymmetric.
5. Solution
We swap indexes in 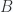 , switch dummy indexes, then swap indexes in
, switch dummy indexes, then swap indexes in 

Our result is the negative of itself, so must be zero.
6. Statement. Characteristic equation for the electromagnetic strength tensor
Show that  is invariant under Lorentz transformations. Consider the polynomial of
is invariant under Lorentz transformations. Consider the polynomial of  , also called the characteristic polynomial of the matrix
, also called the characteristic polynomial of the matrix  . Find the coefficients of the expansion of
. Find the coefficients of the expansion of  in powers of
in powers of 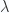 in terms of the components of
in terms of the components of  . Use the result to argue that
. Use the result to argue that  and
and  are Lorentz invariant.
are Lorentz invariant.
6. Solution
The invariance of the determinant
Let’s consider how any lower index rank 2 tensor transforms. Given a transformation of coordinates

where  , and
, and  . Let’s reflect briefly on why this determinant is unit valued. We have
. Let’s reflect briefly on why this determinant is unit valued. We have

which implies that the transformation product is

the identity matrix. The identity matrix has unit determinant, so we must have

Since  we have
we have

which is all that we can say about the determinant of this class of transformations by considering just invariance. If we restrict the transformations of coordinates to those of the same determinant sign as the identity matrix, we rule out reflections in time or space. This seems to be the essence of the  labeling.
labeling.
Why dwell on this? Well, I wanted to be clear on the conventions I’d chosen, since parts of the course notes used  , and
, and  , and gave that matrix unit determinant. That
, and gave that matrix unit determinant. That  looks like it is equivalent to my
looks like it is equivalent to my  , except that the one in the course notes is loose when it comes to lower and upper indexes since it gives
, except that the one in the course notes is loose when it comes to lower and upper indexes since it gives  .
.
I’ll write

and require this (not  ) to be the matrix with unit determinant. Having cleared the index upper and lower confusion I had trying to reconcile the class notes with the rules for index manipulation, let’s now consider the Lorentz transformation of a lower index rank 2 tensor (not necessarily antisymmetric or symmetric)
) to be the matrix with unit determinant. Having cleared the index upper and lower confusion I had trying to reconcile the class notes with the rules for index manipulation, let’s now consider the Lorentz transformation of a lower index rank 2 tensor (not necessarily antisymmetric or symmetric)
We have, transforming in the same fashion as a lower index coordinate four vector (but twice, once for each index)

The determinant of the transformation tensor  is
is

We see that the determinant of a lower index rank 2 tensor is invariant under Lorentz transformation. This would include our characteristic polynomial  .
.
Expanding the determinant.
Utilizing 2.39 we can now calculate the characteristic polynomial. This is

However,  , or
, or  . This means we have
. This means we have

and our determinant is reduced to

If we expand this out we have our powers of 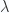 coefficients are
coefficients are

By 2.39 the  coefficient is just
coefficient is just  .
.
The  terms can be seen to be zero. For example, the first one is
terms can be seen to be zero. For example, the first one is

where the final equality to zero comes from summing a symmetric and antisymmetric product.
Similarly the 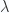 coefficients can be shown to be zero. Again the first as a sample is
coefficients can be shown to be zero. Again the first as a sample is
![\begin{aligned}-\frac{1}{{24}} \epsilon^{s t u v} \epsilon_{a b c d} {\delta^c}_u {F^d}_v {F^a}_s {F^b}_t &=-\frac{1}{{24}} \epsilon^{u s t v} \epsilon_{u a b d} {F^d}_v {F^a}_s {F^b}_t \\ &=-\frac{1}{{24}} \delta^{[s}_a\delta^{t}_b\delta^{v]}_d{F^d}_v {F^a}_s {F^b}_t \\ &=-\frac{1}{{24}} {F^a}_{[s}{F^b}_{t}{F^d}_{v]} \\ \end{aligned}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Baligned%7D-%5Cfrac%7B1%7D%7B%7B24%7D%7D+%5Cepsilon%5E%7Bs+t+u+v%7D+%5Cepsilon_%7Ba+b+c+d%7D+%7B%5Cdelta%5Ec%7D_u+%7BF%5Ed%7D_v+%7BF%5Ea%7D_s+%7BF%5Eb%7D_t+%26%3D-%5Cfrac%7B1%7D%7B%7B24%7D%7D+%5Cepsilon%5E%7Bu+s+t+v%7D+%5Cepsilon_%7Bu+a+b+d%7D+%7BF%5Ed%7D_v+%7BF%5Ea%7D_s+%7BF%5Eb%7D_t++%5C%5C+%26%3D-%5Cfrac%7B1%7D%7B%7B24%7D%7D+%5Cdelta%5E%7B%5Bs%7D_a%5Cdelta%5E%7Bt%7D_b%5Cdelta%5E%7Bv%5D%7D_d%7BF%5Ed%7D_v+%7BF%5Ea%7D_s+%7BF%5Eb%7D_t++%5C%5C+%26%3D-%5Cfrac%7B1%7D%7B%7B24%7D%7D+%7BF%5Ea%7D_%7B%5Bs%7D%7BF%5Eb%7D_%7Bt%7D%7BF%5Ed%7D_%7Bv%5D%7D+%5C%5C+%5Cend%7Baligned%7D+&bg=fafcff&fg=2a2a2a&s=0&c=20201002)
Disregarding the  factor, let’s just expand this antisymmetric sum
factor, let’s just expand this antisymmetric sum
![\begin{aligned}{F^a}_{[a}{F^b}_{b}{F^d}_{d]}&={F^a}_{a}{F^b}_{b}{F^d}_{d}+{F^a}_{d}{F^b}_{a}{F^d}_{b}+{F^a}_{b}{F^b}_{d}{F^d}_{a}-{F^a}_{a}{F^b}_{d}{F^d}_{b}-{F^a}_{d}{F^b}_{b}{F^d}_{a}-{F^a}_{b}{F^b}_{a}{F^d}_{d} \\ &={F^a}_{d}{F^b}_{a}{F^d}_{b}+{F^a}_{b}{F^b}_{d}{F^d}_{a} \\ \end{aligned}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Baligned%7D%7BF%5Ea%7D_%7B%5Ba%7D%7BF%5Eb%7D_%7Bb%7D%7BF%5Ed%7D_%7Bd%5D%7D%26%3D%7BF%5Ea%7D_%7Ba%7D%7BF%5Eb%7D_%7Bb%7D%7BF%5Ed%7D_%7Bd%7D%2B%7BF%5Ea%7D_%7Bd%7D%7BF%5Eb%7D_%7Ba%7D%7BF%5Ed%7D_%7Bb%7D%2B%7BF%5Ea%7D_%7Bb%7D%7BF%5Eb%7D_%7Bd%7D%7BF%5Ed%7D_%7Ba%7D-%7BF%5Ea%7D_%7Ba%7D%7BF%5Eb%7D_%7Bd%7D%7BF%5Ed%7D_%7Bb%7D-%7BF%5Ea%7D_%7Bd%7D%7BF%5Eb%7D_%7Bb%7D%7BF%5Ed%7D_%7Ba%7D-%7BF%5Ea%7D_%7Bb%7D%7BF%5Eb%7D_%7Ba%7D%7BF%5Ed%7D_%7Bd%7D+%5C%5C+%26%3D%7BF%5Ea%7D_%7Bd%7D%7BF%5Eb%7D_%7Ba%7D%7BF%5Ed%7D_%7Bb%7D%2B%7BF%5Ea%7D_%7Bb%7D%7BF%5Eb%7D_%7Bd%7D%7BF%5Ed%7D_%7Ba%7D+%5C%5C+%5Cend%7Baligned%7D+&bg=fafcff&fg=2a2a2a&s=0&c=20201002)
Of the two terms above that were retained, they are the only ones without a zero  factor. Consider the first part of this remaining part of the sum. Employing the metric tensor, to raise indexes so that the antisymmetry of
factor. Consider the first part of this remaining part of the sum. Employing the metric tensor, to raise indexes so that the antisymmetry of  can be utilized, and then finally relabeling all the dummy indexes we have
can be utilized, and then finally relabeling all the dummy indexes we have

This is just the negative of the second term in the sum, leaving us with zero.
Finally, we have for the  coefficient (
coefficient ( )
)
![\begin{aligned}&\epsilon^{s t u v} \epsilon_{a b c d} \Bigl({\delta^c}_u {\delta^d}_v {F^a}_s {F^b}_t +{\delta^a}_s {F^b}_t {\delta^c}_u {F^d}_v +{\delta^b}_t {F^a}_s {\delta^d}_v {F^c}_u \\ &\qquad +{\delta^b}_t {F^a}_s {\delta^c}_u {F^d}_v +{\delta^a}_s {F^b}_t {\delta^d}_v {F^c}_u + {\delta^a}_s {\delta^b}_t {F^c}_u {F^d}_v \Bigr) \\ &=\epsilon^{s t u v} \epsilon_{a b u v} {F^a}_s {F^b}_t +\epsilon^{s t u v} \epsilon_{s b u d} {F^b}_t {F^d}_v +\epsilon^{s t u v} \epsilon_{a t c v} {F^a}_s {F^c}_u \\ &\qquad +\epsilon^{s t u v} \epsilon_{a t u d} {F^a}_s {F^d}_v +\epsilon^{s t u v} \epsilon_{s b c v} {F^b}_t {F^c}_u + \epsilon^{s t u v} \epsilon_{s t c d} {F^c}_u {F^d}_v \\ &=\epsilon^{s t u v} \epsilon_{a b u v} {F^a}_s {F^b}_t +\epsilon^{t v s u } \epsilon_{b d s u} {F^b}_t {F^d}_v +\epsilon^{s u t v} \epsilon_{a c t v} {F^a}_s {F^c}_u \\ &\qquad +\epsilon^{s v t u} \epsilon_{a d t u} {F^a}_s {F^d}_v +\epsilon^{t u s v} \epsilon_{b c s v} {F^b}_t {F^c}_u + \epsilon^{u v s t} \epsilon_{c d s t} {F^c}_u {F^d}_v \\ &=6\epsilon^{s t u v} \epsilon_{a b u v} {F^a}_s {F^b}_t \\ &=6 (2){\delta^{[s}}_a{\delta^{t]}}_b{F^a}_s {F^b}_t \\ &=12{F^a}_{[a} {F^b}_{b]} \\ &=12( {F^a}_{a} {F^b}_{b} - {F^a}_{b} {F^b}_{a} ) \\ &=-12 {F^a}_{b} {F^b}_{a} \\ &=-12 F^{a b} F_{b a} \\ &=12 F^{a b} F_{a b}\end{aligned}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Baligned%7D%26%5Cepsilon%5E%7Bs+t+u+v%7D+%5Cepsilon_%7Ba+b+c+d%7D+%5CBigl%28%7B%5Cdelta%5Ec%7D_u+%7B%5Cdelta%5Ed%7D_v+%7BF%5Ea%7D_s+%7BF%5Eb%7D_t+%2B%7B%5Cdelta%5Ea%7D_s+%7BF%5Eb%7D_t+%7B%5Cdelta%5Ec%7D_u+%7BF%5Ed%7D_v+%2B%7B%5Cdelta%5Eb%7D_t+%7BF%5Ea%7D_s+%7B%5Cdelta%5Ed%7D_v+%7BF%5Ec%7D_u++%5C%5C+%26%5Cqquad+%2B%7B%5Cdelta%5Eb%7D_t+%7BF%5Ea%7D_s+%7B%5Cdelta%5Ec%7D_u+%7BF%5Ed%7D_v+%2B%7B%5Cdelta%5Ea%7D_s+%7BF%5Eb%7D_t+%7B%5Cdelta%5Ed%7D_v+%7BF%5Ec%7D_u+%2B+%7B%5Cdelta%5Ea%7D_s+%7B%5Cdelta%5Eb%7D_t++%7BF%5Ec%7D_u+%7BF%5Ed%7D_v+%5CBigr%29+%5C%5C+%26%3D%5Cepsilon%5E%7Bs+t+u+v%7D+%5Cepsilon_%7Ba+b+u+v%7D+++%7BF%5Ea%7D_s+%7BF%5Eb%7D_t+%2B%5Cepsilon%5E%7Bs+t+u+v%7D+%5Cepsilon_%7Bs+b+u+d%7D++%7BF%5Eb%7D_t++%7BF%5Ed%7D_v+%2B%5Cepsilon%5E%7Bs+t+u+v%7D+%5Cepsilon_%7Ba+t+c+v%7D++%7BF%5Ea%7D_s++%7BF%5Ec%7D_u++%5C%5C+%26%5Cqquad+%2B%5Cepsilon%5E%7Bs+t+u+v%7D+%5Cepsilon_%7Ba+t+u+d%7D++%7BF%5Ea%7D_s++%7BF%5Ed%7D_v+%2B%5Cepsilon%5E%7Bs+t+u+v%7D+%5Cepsilon_%7Bs+b+c+v%7D++%7BF%5Eb%7D_t++%7BF%5Ec%7D_u+%2B+%5Cepsilon%5E%7Bs+t+u+v%7D+%5Cepsilon_%7Bs+t+c+d%7D++++%7BF%5Ec%7D_u+%7BF%5Ed%7D_v+%5C%5C+%26%3D%5Cepsilon%5E%7Bs+t+u+v%7D+%5Cepsilon_%7Ba+b+u+v%7D+++%7BF%5Ea%7D_s+%7BF%5Eb%7D_t+%2B%5Cepsilon%5E%7Bt+v+s+u+%7D+%5Cepsilon_%7Bb+d+s+u%7D++%7BF%5Eb%7D_t++%7BF%5Ed%7D_v+%2B%5Cepsilon%5E%7Bs+u+t+v%7D+%5Cepsilon_%7Ba+c+t+v%7D++%7BF%5Ea%7D_s++%7BF%5Ec%7D_u++%5C%5C+%26%5Cqquad+%2B%5Cepsilon%5E%7Bs+v+t+u%7D+%5Cepsilon_%7Ba+d+t+u%7D++%7BF%5Ea%7D_s++%7BF%5Ed%7D_v+%2B%5Cepsilon%5E%7Bt+u+s+v%7D+%5Cepsilon_%7Bb+c+s+v%7D++%7BF%5Eb%7D_t++%7BF%5Ec%7D_u+%2B+%5Cepsilon%5E%7Bu+v+s+t%7D+%5Cepsilon_%7Bc+d+s+t%7D++++%7BF%5Ec%7D_u+%7BF%5Ed%7D_v+%5C%5C+%26%3D6%5Cepsilon%5E%7Bs+t+u+v%7D+%5Cepsilon_%7Ba+b+u+v%7D+%7BF%5Ea%7D_s+%7BF%5Eb%7D_t++%5C%5C+%26%3D6+%282%29%7B%5Cdelta%5E%7B%5Bs%7D%7D_a%7B%5Cdelta%5E%7Bt%5D%7D%7D_b%7BF%5Ea%7D_s+%7BF%5Eb%7D_t++%5C%5C+%26%3D12%7BF%5Ea%7D_%7B%5Ba%7D+%7BF%5Eb%7D_%7Bb%5D%7D++%5C%5C+%26%3D12%28+%7BF%5Ea%7D_%7Ba%7D+%7BF%5Eb%7D_%7Bb%7D+-+%7BF%5Ea%7D_%7Bb%7D+%7BF%5Eb%7D_%7Ba%7D+%29+%5C%5C+%26%3D-12+%7BF%5Ea%7D_%7Bb%7D+%7BF%5Eb%7D_%7Ba%7D+%5C%5C+%26%3D-12+F%5E%7Ba+b%7D+F_%7Bb+a%7D+%5C%5C+%26%3D12+F%5E%7Ba+b%7D+F_%7Ba+b%7D%5Cend%7Baligned%7D+&bg=fafcff&fg=2a2a2a&s=0&c=20201002)
Therefore, our characteristic polynomial is

Observe that in matrix form our strength tensors are

From these we can compute  easily by inspection
easily by inspection

Computing the determinant is not so easy. The dumb and simple way of expanding by cofactors takes two pages, and yields eventually

That supplies us with a relation for the characteristic polynomial in  and
and 

Observe that we found this for the special case where  and
and  were perpendicular in homework 2. Observe that when we have that perpendicularity, we can solve for the eigenvalues by inspection
were perpendicular in homework 2. Observe that when we have that perpendicularity, we can solve for the eigenvalues by inspection

and were able to diagonalize the matrix  to solve the Lorentz force equation in parametric form. When
to solve the Lorentz force equation in parametric form. When  we had real eigenvalues and an orthogonal diagonalization when
we had real eigenvalues and an orthogonal diagonalization when  . For the
. For the  , we had a two purely imaginary eigenvalues, and when
, we had a two purely imaginary eigenvalues, and when  this was a Hermitian diagonalization. For the general case, when one of
this was a Hermitian diagonalization. For the general case, when one of  , or
, or  was zero, things didn’t have the same nice closed form solution.
was zero, things didn’t have the same nice closed form solution.
In general our eigenvalues are

For the purposes of this problem we really only wish to show that  and
and  are Lorentz invariants. When
are Lorentz invariants. When  we have
we have  , a Lorentz invariant. This must mean that
, a Lorentz invariant. This must mean that  is itself a Lorentz invariant. Since that is invariant, and we require
is itself a Lorentz invariant. Since that is invariant, and we require  to be invariant for any other possible values of
to be invariant for any other possible values of 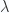 , the difference
, the difference  must also be Lorentz invariant.
must also be Lorentz invariant.
7. Statement. Show that the pseudoscalar invariant has only boundary effects.
Use integration by parts to show that  only depends on the values of
only depends on the values of  at the “boundary” of spacetime (e.g. the “surface” depicted on page 105 of the notes) and hence does not affect the equations of motion for the electromagnetic field.
at the “boundary” of spacetime (e.g. the “surface” depicted on page 105 of the notes) and hence does not affect the equations of motion for the electromagnetic field.
7. Solution
This proceeds in a fairly straightforward fashion

Now, observe that by the Bianchi identity, this second term is zero

Now we have a set of perfect differentials, and can integrate

We are left with a only contributions to the integral from the boundary terms on the spacetime hypervolume, three-volume normals bounding the four-volume integration in the original integral.
8. Statement. Electromagnetic duality transformations.
Show that the Maxwell equations in vacuum are invariant under the transformation:  , where
, where  is the dual electromagnetic stress tensor. Replacing
is the dual electromagnetic stress tensor. Replacing 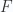 with
with  is known as “electric-magnetic duality”. Explain this name by considering the transformation in terms of
is known as “electric-magnetic duality”. Explain this name by considering the transformation in terms of  and
and  . Are the Maxwell equations with sources invariant under electric-magnetic duality transformations?
. Are the Maxwell equations with sources invariant under electric-magnetic duality transformations?
8. Solution
Let’s first consider the explanation of the name. First recall what the expansions are of  and
and  in terms of
in terms of  and
and  . These are
. These are

with  , and
, and  .
.
The magnetic field components are

with  and
and  .
.
Now let’s expand the dual tensors. These are

and

Summarizing we have

Is there a sign error in the  result? Other than that we have the same sort of structure for the tensor with
result? Other than that we have the same sort of structure for the tensor with 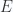 and
and 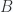 switched around.
switched around.
Let’s write these in matrix form, to compare

From these we can see by inspection that we have

This is consistent with the stated result in [1] (except for a factor of  due to units differences), so it appears the signs above are all kosher.
due to units differences), so it appears the signs above are all kosher.
Now, let’s see if the if the dual tensor satisfies the vacuum equations.

So the first checks out, provided we have no sources. If we have sources, then we see here that Maxwell’s equations do not hold since this would imply that the four current density must be zero.
How about the Bianchi identity? That gives us
![\begin{aligned}\epsilon^{i j k l} \partial_j \tilde{F}_{k l} &=\epsilon^{i j k l} \partial_j \frac{1}{{2}} \epsilon_{k l a b} F^{a b} \\ &=\frac{1}{{2}} \epsilon^{k l i j} \epsilon_{k l a b} \partial_j F^{a b} \\ &=\frac{1}{{2}} (2!) {\delta^i}_{[a} {\delta^j}_{b]} \partial_j F^{a b} \\ &=\partial_j (F^{i j} - F^{j i} ) \\ &=2 \partial_j F^{i j} .\end{aligned}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Baligned%7D%5Cepsilon%5E%7Bi+j+k+l%7D+%5Cpartial_j+%5Ctilde%7BF%7D_%7Bk+l%7D+%26%3D%5Cepsilon%5E%7Bi+j+k+l%7D+%5Cpartial_j+%5Cfrac%7B1%7D%7B%7B2%7D%7D+%5Cepsilon_%7Bk+l+a+b%7D+F%5E%7Ba+b%7D+%5C%5C+%26%3D%5Cfrac%7B1%7D%7B%7B2%7D%7D+%5Cepsilon%5E%7Bk+l+i+j%7D+%5Cepsilon_%7Bk+l+a+b%7D+%5Cpartial_j+F%5E%7Ba+b%7D+%5C%5C+%26%3D%5Cfrac%7B1%7D%7B%7B2%7D%7D+%282%21%29+%7B%5Cdelta%5Ei%7D_%7B%5Ba%7D+%7B%5Cdelta%5Ej%7D_%7Bb%5D%7D+%5Cpartial_j+F%5E%7Ba+b%7D+%5C%5C+%26%3D%5Cpartial_j+%28F%5E%7Bi+j%7D+-+F%5E%7Bj+i%7D+%29+%5C%5C+%26%3D2+%5Cpartial_j+F%5E%7Bi+j%7D+.%5Cend%7Baligned%7D+&bg=fafcff&fg=2a2a2a&s=0&c=20201002)
The factor of two is slightly curious. Is there a mistake above? If there is a mistake, it doesn’t change the fact that Maxwell’s equation

Gives us zero for the Bianchi identity under source free conditions of  .
.
Problem 2. Transformation properties of  and
and  , again.
, again.
1. Statement
Use the form of  from page 82 in the class notes, the transformation law for
from page 82 in the class notes, the transformation law for  given further down that same page, and the explicit form of the
given further down that same page, and the explicit form of the  matrix
matrix  (say, corresponding to motion in the positive
(say, corresponding to motion in the positive  direction with speed
direction with speed  ) to derive the transformation law of the fields
) to derive the transformation law of the fields  and
and  . Use the transformation law to find the electromagnetic field of a charged particle moving with constant speed
. Use the transformation law to find the electromagnetic field of a charged particle moving with constant speed  in the positive
in the positive  direction and check that the result agrees with the one that you obtained in Homework 2.
direction and check that the result agrees with the one that you obtained in Homework 2.
1. Solution
Given a transformation of coordinates

our rank 2 tensor  transforms as
transforms as

Introducing matrices

and noting that  , we can express the electromagnetic strength tensor transformation as
, we can express the electromagnetic strength tensor transformation as

The class notes use  , which violates our conventions on mixed upper and lower indexes, but the end result 3.80 is the same.
, which violates our conventions on mixed upper and lower indexes, but the end result 3.80 is the same.

Writing

we can compute the transformed field strength tensor

As a check we have the antisymmetry that is expected. There is also a regularity to the end result that is aesthetically pleasing, hinting that things are hopefully error free. In coordinates for  and
and  this is
this is

Writing  , we have
, we have

which puts us enroute to a tidier vector form

For a vector  , write
, write  ,
,  , allowing a compact description of the field transformation
, allowing a compact description of the field transformation

Now, we want to consider the field of a moving particle. In the particle’s (unprimed) rest frame the field due to its potential  is
is

Coordinates for a “stationary” observer, who sees this particle moving along the x-axis at speed  are related by a boost in the
are related by a boost in the 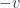 direction
direction

Therefore the fields in the observer frame will be

More explicitly with  this is
this is

Comparing to Problem 3 in Problem set 2, I see that this matches the result obtained by separately transforming the gradient, the time partial, and the scalar potential. Actually, if I am being honest, I see that I made a sign error in all the coordinates of  when I initially did (this ungraded problem) in problem set 2. That sign error should have been obvious by considering the
when I initially did (this ungraded problem) in problem set 2. That sign error should have been obvious by considering the  case which would have mysteriously resulted in inversion of all the coordinates of the observed electric field.
case which would have mysteriously resulted in inversion of all the coordinates of the observed electric field.
2. Statement
A particle is moving with velocity  in perpendicular
in perpendicular  and
and  fields, all given in some particular “stationary” frame of reference.
fields, all given in some particular “stationary” frame of reference.
\begin{enumerate}
\item Show that there exists a frame where the problem of finding the particle trajectory can be reduced to having either only an electric or only a magnetic field.
\item Explain what determines which case takes place.
\item Find the velocity  of that frame relative to the “stationary” frame.
of that frame relative to the “stationary” frame.
\end{enumerate}
2. Solution
\paragraph{Part 1 and 2:} Existence of the transformation.
In the single particle Lorentz trajectory problem we wish to solve

which in matrix form we can write as

where we write our column vector proper velocity as  . Under transformation of coordinates
. Under transformation of coordinates  , with
, with  , this becomes
, this becomes

Suppose we can find eigenvectors for the matrix  . That is for some eigenvalue
. That is for some eigenvalue 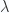 , we can find an eigenvector
, we can find an eigenvector 

Rearranging we have

and conclude that  lies in the null space of the matrix
lies in the null space of the matrix  and that this difference of matrices must have a zero determinant
and that this difference of matrices must have a zero determinant

Since  for any Lorentz transformation
for any Lorentz transformation  in
in  , and
, and  we have
we have

In problem 1.6, we called this our characteristic equation  . Observe that the characteristic equation is Lorentz invariant for any
. Observe that the characteristic equation is Lorentz invariant for any 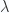 , which requires that the eigenvalues
, which requires that the eigenvalues 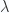 are also Lorentz invariants.
are also Lorentz invariants.
In problem 1.6 of this problem set we computed that this characteristic equation expands to

The eigenvalues for the system, also each necessarily Lorentz invariants, are

Observe that in the specific case where  , as in this problem, we must have
, as in this problem, we must have  in all frames, and the two non-zero eigenvalues of our characteristic polynomial are simply
in all frames, and the two non-zero eigenvalues of our characteristic polynomial are simply

These and  are the invariants for this system. If we have
are the invariants for this system. If we have  in one frame, we must also have
in one frame, we must also have  in another frame, still maintaining perpendicular fields. In particular if
in another frame, still maintaining perpendicular fields. In particular if  we maintain real eigenvalues. Similarly if
we maintain real eigenvalues. Similarly if  in some frame, we must always have imaginary eigenvalues, and this is also true in the
in some frame, we must always have imaginary eigenvalues, and this is also true in the  case.
case.
While the problem can be posed as a pure diagonalization problem (and even solved numerically this way for the general constant fields case), we can also work symbolically, thinking of the trajectories problem as simply seeking a transformation of frames that reduce the scope of the problem to one that is more tractable. That does not have to be the linear transformation that diagonalizes the system. Instead we are free to transform to a frame where one of the two fields  or
or  is zero, provided the invariants discussed are maintained.
is zero, provided the invariants discussed are maintained.
\paragraph{Part 3:} Finding the boost velocity that wipes out one of the fields.
Let’s now consider a Lorentz boost  , and seek to solve for the boost velocity that wipes out one of the fields, given the invariants that must be maintained for the system
, and seek to solve for the boost velocity that wipes out one of the fields, given the invariants that must be maintained for the system
To make things concrete, suppose that our perpendicular fields are given by  and
and  .
.
Let also assume that we can find the velocity  for which one or more of the transformed fields is zero. Suppose that velocity is
for which one or more of the transformed fields is zero. Suppose that velocity is

where  are the direction cosines of
are the direction cosines of  so that
so that  . We will want to compute the components of
. We will want to compute the components of  and
and  parallel and perpendicular to this velocity.
parallel and perpendicular to this velocity.
Those are


For the magnetic field we have

and

Now, observe that  , but this is just zero. So we have
, but this is just zero. So we have  . So our cross products terms are just
. So our cross products terms are just

We can now express how the fields transform, given this arbitrary boost velocity. From 3.97, this is

Zero Electric field case.
Let’s tackle the two cases separately. First when  , we can transform to a frame where
, we can transform to a frame where  . In coordinates from 3.117 this supplies us three sets of equations. These are
. In coordinates from 3.117 this supplies us three sets of equations. These are

With an assumed solution the 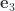 coordinate equation implies that one of
coordinate equation implies that one of 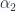 or
or  is zero. Perhaps there are solutions with
is zero. Perhaps there are solutions with  too, but inspection shows that
too, but inspection shows that  nicely kills off the first equation. Since
nicely kills off the first equation. Since  , that also implies that we are left with
, that also implies that we are left with

Or

Our velocity was  solving the problem for the
solving the problem for the  case up to an adjustable constant
case up to an adjustable constant  . That constant comes with constraints however, since we must also have our cosine
. That constant comes with constraints however, since we must also have our cosine  . Expressed another way, the magnitude of the boost velocity is constrained by the relation
. Expressed another way, the magnitude of the boost velocity is constrained by the relation

It appears we may also pick the equality case, so one velocity (not unique) that should transform away the electric field is

This particular boost direction is perpendicular to both fields. Observe that this highlights the invariance condition  since we see this is required for a physically realizable velocity. Boosting in this direction will reduce our problem to one that has only the magnetic field component.
since we see this is required for a physically realizable velocity. Boosting in this direction will reduce our problem to one that has only the magnetic field component.
Zero Magnetic field case.
Now, let’s consider the case where we transform the magnetic field away, the case when our characteristic polynomial has strictly real eigenvalues  . In this case, if we write out our equations for the transformed magnetic field and require these to separately equal zero, we have
. In this case, if we write out our equations for the transformed magnetic field and require these to separately equal zero, we have

Similar to before we see that  kills off the first and second equations, leaving just
kills off the first and second equations, leaving just

We now have a solution for the family of direction vectors that kill the magnetic field off

In addition to the initial constraint that  , we have as before, constraints on the allowable values of
, we have as before, constraints on the allowable values of 

Like before we can pick the equality  , yielding a boost direction of
, yielding a boost direction of

Again, we see that the invariance condition  is required for a physically realizable velocity if that velocity is entirely perpendicular to the fields.
is required for a physically realizable velocity if that velocity is entirely perpendicular to the fields.
Problem 3. Continuity equation for delta function current distributions.
Statement
Show explicitly that the electromagnetic 4-current  for a particle moving with constant velocity (considered in class, p. 100-101 of notes) is conserved
for a particle moving with constant velocity (considered in class, p. 100-101 of notes) is conserved  . Give a physical interpretation of this conservation law, for example by integrating
. Give a physical interpretation of this conservation law, for example by integrating  over some spacetime region and giving an integral form to the conservation law (
over some spacetime region and giving an integral form to the conservation law ( is known as the “continuity equation”).
is known as the “continuity equation”).
Solution
First lets review. Our four current was defined as

If each of the trajectories  represents constant motion we have
represents constant motion we have

The spacetime split of this four vector is

with differentials

Writing out the delta functions explicitly we have

So our time and space components of the current can be written

Each of these integrals can be evaluated with respect to the time coordinate delta function leaving the distribution

With this more general expression (multi-particle case) it should be possible to show that the four divergence is zero, however, the problem only asks for one particle. For the one particle case, we can make things really easy by taking the initial point in space and time as the origin, and aligning our velocity with one of the coordinates (say  ).
).
Doing so we have the result derived in class

Our divergence then has only two portions

and these cancel out when summed. Note that this requires us to be loose with our delta functions, treating them like regular functions that are differentiable.
For the more general multiparticle case, we can treat the sum one particle at a time, and in each case, rotate coordinates so that the four divergence only picks up one term.
As for physical interpretation via integral, we have using the four dimensional divergence theorem

where  is the three-volume element perpendicular to a
is the three-volume element perpendicular to a  plane. These volume elements are detailed generally in the text [2], however, they do note that one special case specifically
plane. These volume elements are detailed generally in the text [2], however, they do note that one special case specifically  , the element of the three-dimensional (spatial) volume “normal” to hyperplanes
, the element of the three-dimensional (spatial) volume “normal” to hyperplanes  .
.
Without actually computing the determinants, we have something that is roughly of the form

This is cheating a bit to just write  . Are there specific orientations required by the metric. To be precise we’d have to calculate the determinants detailed in the text, and then do the duality transformations.
. Are there specific orientations required by the metric. To be precise we’d have to calculate the determinants detailed in the text, and then do the duality transformations.
Per unit time, we can write instead

Rather loosely this appears to roughly describe that the rate of change of charge in a volume must be matched with the “flow” of current through the surface within that amount of time.
References
[1] Wikipedia. Electromagnetic tensor — wikipedia, the free encyclopedia [online]. 2011. [Online; accessed 27-February-2011]. http://en.wikipedia.org/w/index.php?title=Electromagnetic_tensor&oldid=414989505.
[2] L.D. Landau and E.M. Lifshitz. The classical theory of fields. Butterworth-Heinemann, 1980.
. If we expand out
we see that matches
substition, and comparision of this with the Euler-Lagrange result above completes the exersize.
we have
we also have
we take the derivative
are
, so this is just