May 2024
M	T	W	T	F	S	S
	1	2	3	4	5
6	7	8	9	10	11	12
13	14	15	16	17	18	19
20	21	22	23	24	25	26
27	28	29	30	31

Posts Tagged ‘PHY450’

updates to my old class notes from the 2011 phy450h1s (relativistic electrodynamics)

Posted by peeterjoot on June 2, 2012

I’ve made some minor updates to my old class notes from the 2011 phy450h1s (relativistic electrodynamics) course I took:

https://sites.google.com/site/peeterjoot/math2011/phy450.pdf

(I’ve switched this notes collection, as well as some others, to a better looking latex book template, one that I also used for my continuum mechanics class notes). While making that change I also switched things from a chapter heading per lecture, to a couple more logical chapter headings, which makes things easier to navigate.

Posted in Math and Physics Learning. | Tagged: PHY450, relativistic electrodynamics | 2 Comments »

Final collection of class notes for the 2011 Relativistic Electrodynamics (phy450hs1) course I attended at UofT

Posted by peeterjoot on May 5, 2011

CLICK HERE for my final collection of class notes for the 2011 Relativistic Electrodynamics (phy450hs1) course I attended at UofT. This course was taught by Prof. Erich Poppitz, and TA’ed by Simon Freedman, and provided a structured top down approach to electrodynamics. Starting with very few basic principles a great deal of material was covered in a very refreshing hierarchical fashion.

Typos and errors, if any, are probably mine (Peeter), and no claim nor attempt of spelling or grammar correctness will be made.

The text for the course was Landau and Lifshitz, “Classical Theory of Fields”.

These notes track along with the Professor’s hand written notes very closely, since his lectures follow his notes very closely. While I used the note taking exercise as a way to verify that I understood all the day’s lecture materials, the Professor’s notes are in many instances a much better study resource, since there are details in his notes that were left for us to read, and not necessarily covered in the lectures. On the other hand, there are details in these notes that I’ve added when I didn’t find his approach simplistic enough for me to grasp, or I failed to follow the details in class.

This also has some private notes from my reading of the text and some thoughts on materials we were covering. One of the earlier of these was due to unfortunate use of an ancient edition of the text borrowed from the library, since mine had been lost in shipping. That version didn’t use the upper and lower index quantities that I’d expected, so I tried to puzzle out some of what myself from what I knew. Once I got an up to date copy of the text the point of that exercise was negated.

Also included are some assigned problems, at least the parts of them that I did not hand write. I’ve corrected some the errors after receiving grading feedback, and where I haven’t done so I at least recorded some of the grading comments as a reference. Not all the problems were graded, so I make no guarantees of correctness.

Included in the PDF above are all the following individual PDFs. These are still available, but may contain errors possibly fixed in the complete notes collection.

April 13, 2011 Some exam reflection.

April 10, 2011 Three dimensional divergence theorem with generally parametrized volume element.

April 6, 2011 PHY450H1S. Relativistic Electrodynamics Lecture 27. Radiation reaction force continued, and limits of classical electrodynamics.

April 5, 2011 PHY450H1S. Relativistic Electrodynamics Lecture 26. Radiation reaction force for a dipole system.

Mar 31, 2011 PHY450H1S. Relativistic Electrodynamics Lecture 25. Second order interaction, the Darwin Lagrangian.

Mar 30, 2011 PHY450H1S. Relativistic Electrodynamics Tutorial 9. Some worked problems. EM reflection. Stress energy tensor for simple configurations.

Mar 30, 2011 PHY450H1S. Relativistic Electrodynamics Lecture 24. Non-relativistic electrostatic Lagrangian.

Mar 29, 2011 PHY450H1S. Relativistic Electrodynamics Lecture 23. Energy Momentum Tensor.

Mar 25, 2011 Problem Set 6.

Mar 23, 2011 PHY450H1S. Relativistic Electrodynamics Tutorial 8. EM fields from magnetic dipole current.

Mar 23, 2011 Energy Momentum Tensor.

Mar 22, 2011 PHY450H1S. Relativistic Electrodynamics Lecture 21. More on EM fields due to dipole radiation.

Mar 15, 2011 PHY450H1S. Relativistic Electrodynamics Lecture 19. Lienard-Wiechert potentials.

Mar 15, 2011 PHY450H1S. Relativistic Electrodynamics Lecture 20. Potentials at a distance from a localized current distribution. EM fields due to dipole radiation.

Mar 14, 2011 Problem Set 5.

Mar 10, 2011 PHY450H1S. Relativistic Electrodynamics Tutorial 5. Angular momentum of EM fields

Mar 9, 2011 PHY450H1S. Relativistic Electrodynamics Lecture 18. Green’s function solution to Maxwell’s equation.

Mar 8, 2011 Playing with complex notation for relativistic applications in a plane

Mar 8, 2011 PHY450H1S. Relativistic Electrodynamics Lecture 17. Energy and momentum density. Starting a Green’s function solution to Maxwell’s equation.

Mar 3, 2011 PHY450H1S. Relativistic Electrodynamics Tutorial 4. Waveguides: confined EM waves.

Mar 3, 2011 PHY450H1S Problem Set 4.

Mar 2, 2011 PHY450H1S. Relativistic Electrodynamics Lecture 16. Monochromatic EM fields. Poynting vector and energy density conservation.

Mar 1, 2011 PHY450H1S. Relativistic Electrodynamics Lecture 15. Fourier solution of Maxwell’s vacuum wave equation in the Coulomb gauge.

Feb 16, 2011 PHY450H1S. Relativistic Electrodynamics Lecture 14 (Taught by Simon Freedman). Wave equation in Coulomb and Lorentz gauges.

Feb 15, 2011 PHY450H1S. Relativistic Electrodynamics Lecture 13. Variational principle for the field.

Feb 15, 2011 PHY450H1S Problem Set 3.

Feb 10, 2011 PHY450H1S. Relativistic Electrodynamics Lecture 12. Action for the field.

Feb 9, 2011 PHY450H1S. Relativistic Electrodynamics Lecture 11. Unpacking Lorentz force equation. Lorentz transformations of the strength tensor, Lorentz field invariants, Bianchi identity, and first half of Maxwell’s.

Feb 8, 2011 PHY450H1S. Relativistic Electrodynamics Lecture 10. Lorentz force equation energy term, and four vector formulation of the Lorentz force equation.

Feb 6, 2011 Energy term of the Lorentz force equation.

Feb 3, 2011 PHY450H1S. Relativistic Electrodynamics Tutorial 3. Relativistic motion in constant uniform electric or magnetic fields.

Feb 1, 2011 PHY450H1S Problem Set 2.

Feb 1, 2011 PHY450H1S. Relativistic Electrodynamics Lecture 9. Dynamics in a vector field.

Feb 1, 2011 PHY450H1S. Relativistic Electrodynamics Lecture 8. Relativistic dynamics.

Jan 27, 2011 PHY450H1S. Relativistic Electrodynamics Tutorial 2. Two worked problems.

Jan 26, 2011 PHY450H1S. Relativistic Electrodynamics Lecture 7. Action and relativistic dynamics.

Jan 25, 2011 PHY450H1S. Relativistic Electrodynamics Lecture 6. Four vectors and tensors.

Jan 22, 2011 PHY450H1S Problem Set 1.

Jan 20, 2011 Four vectors and a worked problem on energy flux density.

Jan 18, 2011 Proper time, length contraction, time dialation, causality.

Jan 18, 2011 Spacetime geometry, Lorentz transformations, Minkowski diagrams.

Jan 14, 2011 Lorentz transformation of an antisymmetric tensor.

Jan 13, 2011 Spacetime, events, worldlines, spacetime intervals, and invariance.

Jan 12, 2011 Spacetime, events, worldlines, proper time, invariance.

Jan 11, 2011 Speed of light and simultaneity.

Posted in Math and Physics Learning. | Tagged: PHY450, relativistic electrodynamics | Leave a Comment »

PHY450H1S. Relativistic Electrodynamics Lecture 27 (Taught by Prof. Erich Poppitz). Radiation reaction force continued, and limits of classical electrodynamics.

Posted by peeterjoot on May 3, 2011

[Click here for a PDF of this post with nicer formatting (especially if my latex to wordpress script has left FORMULA DOES NOT PARSE errors.)]

Reading.

Covering chapter 8 section 65 material from the text [1].

FIXME: Covering pp. 198.1-200: (last topic): attempt to go to the next order $(v/c)^3$ – radiation damping, the limitations of classical electrodynamics, and the relevant time/length/energy scales.

Radiation reaction force.

We previously obtained the radiation reaction force by adding a “frictional” force to the harmonic oscillator system. Now its time to obtain this by continuing the expansion of the potentials to the next order in $\mathbf{v}/c$ .

Recall that our potentials are

$\begin{aligned}\phi(\mathbf{x}, t) &= \int d^3 \mathbf{x} \frac{\rho\left(\mathbf{x}', t - {\left\lvert{\mathbf{x} - \mathbf{x}'}\right\rvert}/c\right)}{{\left\lvert{\mathbf{x} - \mathbf{x}}\right\rvert}} \\ \mathbf{A}(\mathbf{x}, t) &= \frac{1}{{c}}\int d^3 \mathbf{x} \frac{\mathbf{j}\left(\mathbf{x}', t - {\left\lvert{\mathbf{x} - \mathbf{x}'}\right\rvert}/c\right)}{{\left\lvert{\mathbf{x} - \mathbf{x}}\right\rvert}}.\end{aligned} \hspace{\stretch{1}}(2.1)$

We can expand in Taylor series about $t$ . For the charge density this is

$\begin{aligned}\begin{aligned}\rho&\left(\mathbf{x}', t - {\left\lvert{\mathbf{x} - \mathbf{x}'}\right\rvert}/c\right) \\ &\approx \rho(\mathbf{x}', t) - \frac{{\left\lvert{\mathbf{x} - \mathbf{x}'}\right\rvert}}{c} \frac{\partial {}}{\partial {t}} \rho(\mathbf{x}', t) + \frac{1}{{2}} \left(\frac{{\left\lvert{\mathbf{x} - \mathbf{x}'}\right\rvert}}{c}\right)^2 \frac{\partial^2 {{}}}{\partial {{t}}^2} \rho(\mathbf{x}', t) - \frac{1}{{6}} \left(\frac{{\left\lvert{\mathbf{x} - \mathbf{x}'}\right\rvert}}{c}\right)^3 \frac{\partial^3}{\partial t^3} \rho(\mathbf{x}', t) \end{aligned},\end{aligned} \hspace{\stretch{1}}(2.3)$

so that our scalar potential to third order is

$\begin{aligned}\phi(\mathbf{x}, t) &=\int d^3 \mathbf{x} \frac{\rho(\mathbf{x}', t) }{{\left\lvert{\mathbf{x} - \mathbf{x}'}\right\rvert}}- \frac{{\left\lvert{\mathbf{x} - \mathbf{x}'}\right\rvert}}{c} \frac{\partial {}}{\partial {t}} \int d^3 \mathbf{x} \frac{\rho(\mathbf{x}', t) }{{\left\lvert{\mathbf{x} - \mathbf{x}'}\right\rvert}} \\ &+ \frac{1}{{2}} \left(\frac{{\left\lvert{\mathbf{x} - \mathbf{x}'}\right\rvert}}{c}\right)^2 \frac{\partial^2 {{}}}{\partial {{t}}^2} \int d^3 \mathbf{x} \frac{\rho(\mathbf{x}', t) }{{\left\lvert{\mathbf{x} - \mathbf{x}'}\right\rvert}}- \frac{1}{{6}} \left(\frac{{\left\lvert{\mathbf{x} - \mathbf{x}'}\right\rvert}}{c}\right)^3 \frac{\partial^3}{\partial t^3} \int d^3 \mathbf{x} \frac{\rho(\mathbf{x}', t) }{{\left\lvert{\mathbf{x} - \mathbf{x}'}\right\rvert}} \\ &=\int d^3 \mathbf{x} \frac{\rho(\mathbf{x}', t) }{{\left\lvert{\mathbf{x} - \mathbf{x}'}\right\rvert}}- {\frac{\partial {}}{\partial {t}} \int d^3 \mathbf{x} \frac{\rho(\mathbf{x}', t) }{{\left\lvert{\mathbf{x} - \mathbf{x}'}\right\rvert}} \frac{{\left\lvert{\mathbf{x} - \mathbf{x}'}\right\rvert}}{c} }\\ &+ \frac{1}{{2}} \frac{\partial^2 {{}}}{\partial {{t}}^2} \int d^3 \mathbf{x} \frac{\rho(\mathbf{x}', t) }{{\left\lvert{\mathbf{x} - \mathbf{x}'}\right\rvert}}\left(\frac{{\left\lvert{\mathbf{x} - \mathbf{x}'}\right\rvert}}{c}\right)^2 - \frac{1}{{6}} \frac{\partial^3}{\partial t^3} \int d^3 \mathbf{x} \frac{\rho(\mathbf{x}', t) }{{\left\lvert{\mathbf{x} - \mathbf{x}'}\right\rvert}} \left(\frac{{\left\lvert{\mathbf{x} - \mathbf{x}'}\right\rvert}}{c}\right)^3 \\ &= \phi^{(0)} + \phi^{(2)} + \phi^{(3)}\end{aligned}$

Expanding the vector potential in Taylor series to second order we have

$\begin{aligned}\mathbf{A}(\mathbf{x}, t) &=\frac{1}{{c}} \int d^3 \mathbf{x} \frac{\mathbf{j}(\mathbf{x}', t) }{{\left\lvert{\mathbf{x} - \mathbf{x}'}\right\rvert}}- \frac{1}{{c}} \frac{{\left\lvert{\mathbf{x} - \mathbf{x}'}\right\rvert}}{c} \frac{\partial {}}{\partial {t}} \int d^3 \mathbf{x} \frac{\mathbf{j}(\mathbf{x}', t) }{{\left\lvert{\mathbf{x} - \mathbf{x}'}\right\rvert}} \\ &=\frac{1}{{c}} \int d^3 \mathbf{x} \frac{\mathbf{j}(\mathbf{x}', t) }{{\left\lvert{\mathbf{x} - \mathbf{x}'}\right\rvert}}- \frac{1}{{c^2}} \frac{\partial {}}{\partial {t}} \int d^3 \mathbf{x} \mathbf{j}(\mathbf{x}', t) \\ &= \mathbf{A}^{(1)} + \mathbf{A}^{(2)} \end{aligned}$

We’ve already considered the effects of the $\mathbf{A}^{(1)}$ term, and now move on to $\mathbf{A}^{(2)}$ . We will write $\phi^{(3)}$ as a total derivative

$\begin{aligned}\phi^{(3)} = \frac{1}{{c}} \frac{\partial {}}{\partial {t}} \left( - \frac{1}{{6 c^2}} \frac{\partial^2}{\partial t^2} \int d^3 \mathbf{x} \rho(\mathbf{x}', t){\left\lvert{\mathbf{x} - \mathbf{x}'}\right\rvert}^2\right)= \frac{1}{{c}} \frac{\partial {}}{\partial {t}} f^{(2)}(\mathbf{x}, t)\end{aligned} \hspace{\stretch{1}}(2.4)$

and gauge transform it away as we did with $\phi^{(2)}$ previously.

$\begin{aligned}\phi^{(3)'} &= \phi^{(3)} - \frac{1}{{c}} \frac{\partial {f^{(2)}}}{\partial {t}} = 0 \\ \mathbf{A}^{(2)'} &= \mathbf{A}^{(2)} + \boldsymbol{\nabla} f^{(2)} \end{aligned} \hspace{\stretch{1}}(2.5)$

$\begin{aligned}\mathbf{A}^{(2)'} &= - \frac{1}{{c^2}} \frac{\partial {}}{\partial {t}} \int d^3 \mathbf{x} \mathbf{j}(\mathbf{x}', t) - \frac{1}{{6 c^2}} \frac{\partial^2}{\partial t^2} \int d^3 \mathbf{x} \rho(\mathbf{x}', t)\boldsymbol{\nabla}_{\mathbf{x}} {\left\lvert{\mathbf{x} - \mathbf{x}'}\right\rvert}^2 \\ \end{aligned}$

Looking first at the first integral we can employ the trick of writing $\mathbf{e}_\alpha = {\partial {\mathbf{x}'}}/{\partial {x^{\alpha'}}}$ , and then employ integration by parts

$\begin{aligned}\int_V d^3 \mathbf{x} \mathbf{j}(\mathbf{x}', t) &=\int_V d^3 \mathbf{x} \mathbf{e}_\alpha j^\alpha (\mathbf{x}', t) \\ &=\int_V d^3 \mathbf{x} \frac{\partial {\mathbf{x}'}}{\partial {x^{\alpha'}}}j^\alpha (\mathbf{x}', t) \\ &=\int_V d^3 \mathbf{x} \frac{\partial {}}{\partial {x^{\alpha'}}} \left( \mathbf{x}' j^\alpha (\mathbf{x}', t) \right)-\int_V d^3 \mathbf{x}\mathbf{x}' \frac{\partial {}}{\partial {x^{\alpha'}}} j^\alpha (\mathbf{x}', t) \\ &=\int_{\partial V} d^2 \boldsymbol{\sigma} \cdot \left( \mathbf{x}' j^\alpha (\mathbf{x}', t) \right)-\int d^3 \mathbf{x} \mathbf{x}' -\frac{\partial {}}{\partial {t}} \rho(\mathbf{x}', t) \\ &=\frac{\partial {}}{\partial {t}} \int d^3 \mathbf{x} \mathbf{x}' \rho(\mathbf{x}', t) \\ \end{aligned}$

For the second integral, we have

$\begin{aligned}\boldsymbol{\nabla}_{\mathbf{x}} {\left\lvert{\mathbf{x} - \mathbf{x}'}\right\rvert}^2 &= \mathbf{e}_\alpha \partial_\alpha (x^\beta - x^{\beta'})(x^\beta - x^{\beta'}) \\ &=2 \mathbf{e}_\alpha \delta_{\alpha \beta}(x^\beta - x^{\beta'}) \\ &= 2 (\mathbf{x} - \mathbf{x}'),\end{aligned}$

so our gauge transformed vector potential term is reduced to

$\begin{aligned}\mathbf{A}^{(2)'} &= -\frac{1}{{c^2}} \frac{\partial^2}{\partial t^2} \int d^3 \mathbf{x} \rho(\mathbf{x}', t) \left(\mathbf{x}' + \frac{1}{{3}}(\mathbf{x} - \mathbf{x}') \right) \\ &= -\frac{1}{{c^2}} \frac{\partial^2}{\partial t^2} \int d^3 \mathbf{x} \rho(\mathbf{x}', t) \left(\frac{1}{{3}} \mathbf{x} + \frac{2}{3}\mathbf{x}' \right) \\ \end{aligned}$

Now we wish to employ a discrete representation of the charge density

$\begin{aligned}\rho(\mathbf{x}', t) = \sum_{b=1}^N q_b \delta^3(\mathbf{x}' - \mathbf{x}_b(t))\end{aligned} \hspace{\stretch{1}}(2.7)$

So that the second order vector potential becomes

$\begin{aligned}\mathbf{A}^{(2)'} &= -\frac{1}{{c^2}} \frac{\partial^2}{\partial t^2} \int d^3 \mathbf{x} \left(\frac{1}{{3}} \mathbf{x} + \frac{2}{3}\mathbf{x}' \right) \sum_{b=1}^N q_b \delta^3(\mathbf{x}' - \mathbf{x}_b(t)) \\ &= -\frac{1}{{c^2}} \frac{\partial^2}{\partial t^2} \sum_{b=1}^N q_b \left( {\frac{1}{{3}} \mathbf{x}} + \frac{2}{3}\mathbf{x}_b(t) \right) \\ &=-\frac{2}{3 c^2} \sum_{b=1}^N q_b \dot{d}{\mathbf{x}}_b(t) \\ &=-\frac{2}{3 c^2} \frac{d^2}{dt^2}\left( \sum_{b=1}^N q_b \mathbf{x}_b(t) \right).\end{aligned}$

We end up with a dipole moment

$\begin{aligned}\mathbf{d}(t) = \sum_{b=1}^N q_b \mathbf{x}_b(t) \end{aligned} \hspace{\stretch{1}}(2.8)$

so we can write

$\begin{aligned}\mathbf{A}^{(2)'} = -\frac{2}{3 c^2} \dot{d}{\mathbf{d}}(t).\end{aligned} \hspace{\stretch{1}}(2.9)$

Observe that there is no magnetic field due to this contribution since there is no explicit spatial dependence

$\begin{aligned}\boldsymbol{\nabla} \times \mathbf{A}^{(2)'} = 0\end{aligned} \hspace{\stretch{1}}(2.10)$

we have also gauge transformed away the scalar potential contribution so have only the time derivative contribution to the electric field

$\begin{aligned}\mathbf{E} = -\frac{1}{{c}} \frac{\partial {\mathbf{A}}}{\partial {t}} - {\boldsymbol{\nabla} \phi} = \frac{2}{3 c^2} \dddot{\mathbf{d}}(t).\end{aligned} \hspace{\stretch{1}}(2.11)$

To $O((v/c)^3)$ there is a homogeneous electric field felt by all particles, hence every particle feels a “friction” force

$\begin{aligned}\mathbf{f}_{\text{rad}} = q \mathbf{E} = \frac{2 q}{3 c^3} \dddot{\mathbf{d}}(t).\end{aligned} \hspace{\stretch{1}}(2.12)$

Moral: $\mathbf{f}_{\text{rad}}$ arises in third order term $O((v/c)^3)$ expansion and thus shouldn’t be given a weight as important as the two other terms. i.e. It’s consequences are less.

Example: our dipole system

$\begin{aligned}m \dot{d}{z} &= - m \omega^2 a + \frac{2 e^2}{3 c^3} \dddot{z} \\ &= - m \omega^2 a + \frac{2 m}{3 c} \frac{e^2}{m c^2} \dddot{z} \\ &= - m \omega^2 a + \frac{2 m}{3} \frac{r_e}{c} \dddot{z} \\ \end{aligned}$

Here $r_e \sim 10^{-13} \text{cm}$ is the classical radius of the electron. For periodic motion

$\begin{aligned}z &\sim e^{i \omega t} z_0 \\ \dot{d}{z} &\sim \omega^2 z_0 \\ \dddot{z} &\sim \omega^3 z_0.\end{aligned}$

The ratio of the last term to the inertial term is

$\begin{aligned}\sim \frac{ \omega^3 m (r_e/c) z_0 }{ m \omega^2 z_0 } \sim \omega \frac{r_e}{c} \ll 1,\end{aligned} \hspace{\stretch{1}}(2.13)$

$\begin{aligned}\omega &\ll \frac{c}{r_e} \\ &\sim \frac{1}{{\tau_e}} \\ &\sim \frac{ 10^{10} \text{cm}/\text{s}}{10^{-13} \text{cm}} \\ &\sim 10^{23} \text{Hz} \\ \end{aligned}$

So long as $\omega \ll 10^{23} \text{Hz}$ , this approximation is valid.

Limits of classical electrodynamics.

What sort of energy is this? At these frequencies QM effects come in

$\begin{aligned}\hbar \sim 10^{-33} \text{J} \cdot \text{s} \sim 10^{-15} \text{eV} \cdot \text{s}\end{aligned} \hspace{\stretch{1}}(3.14)$

$\begin{aligned}\hbar \omega_{max} \sim 10^{-15} \text{eV} \cdot \text{s} \times 10^{23} \frac{1}{{\text{s}}} \sim 10^8 \text{eV} \sim 100 \text{MeV}\end{aligned} \hspace{\stretch{1}}(3.15)$

whereas the rest energy of the electron is

$\begin{aligned}m_e c^2 \sim \frac{1}{{2}} \text{MeV} \sim \text{MeV}.\end{aligned} \hspace{\stretch{1}}(3.16)$

At these frequencies it is possible to create $e^{+}$ and $e^{-}$ pairs. A theory where the number of particles (electrons and positrons) is NOT fixed anymore is required. An estimate of this frequency, where these effects have to be considered is possible.

PICTURE: different length scales with frequency increasing to the left and length scales increasing to the right.

\begin{itemize}
\item $10^{-13} \text{cm}$ , $r_e = e^2/m c^2$ . LHC exploration.
\item $137 \times 10^{-13} \text{cm}$ , $\hbar/m_e c \sim \lambda/2\pi$ , the Compton wavelength of the electron. QED and quantum field theory.
\item $(137)^2 \times 10^{-13} \text{cm} \sim 10^{-10} \text{cm}$ , Bohr radius. QM, and classical electrodynamics.
\end{itemize}

here

$\begin{aligned}\alpha = \frac{e^2}{4 \pi \epsilon_0 \hbar c } = \frac{1}{{137}},\end{aligned} \hspace{\stretch{1}}(3.17)$

is the fine structure constant.

Similar to the distance scale restrictions, we have field strength restrictions. A strong enough field (Electric) can start creating electron and positron pairs. This occurs at about

$\begin{aligned}e E \lambda/2\pi \sim 2 m_e c^2 \end{aligned} \hspace{\stretch{1}}(3.18)$

so the critical field strength is

$\begin{aligned}E_{\text{crit}} &\sim \frac{m_e c^2 }{\lambda/2\pi e} \\ &\sim \frac{m_e c^2 }{\hbar e} m_e c \\ &\sim \frac{m_e^2 c^3}{\hbar e}\end{aligned}$

Is this real?

Yes, with a very heavy nucleus with some electrons stripped off, the field can be so strong that positron and electron pairs will be created. This can be observed in heavy ion collisions!

References

[1] L.D. Landau and E.M. Lifshitz. The classical theory of fields. Butterworth-Heinemann, 1980.

Posted in Math and Physics Learning. | Tagged: PHY450, radiation reaction force | Leave a Comment »

Lienard-Wiechert potentials: Charged particle in a circle one last time (and this time I mean it).

Posted by peeterjoot on May 3, 2011

[Click here for a PDF of this post with nicer formatting (especially if my latex to wordpress script has left FORMULA DOES NOT PARSE errors.)]

Charged particle in a circle without Geometric Algebra.

I tried the problem of calculating the Lienard-Wiechert potentials for circular motion once again in [1] but with the added generalization that allowed the particle to have radial or z-axis motion. Really that was no longer a circular motion problem, but really just a calculation where I was playing with the use of cylindrical coordinates to describe the motion.

It occurred to me that this can be done without any use of Geometric Algebra (or Pauli matrices), which is probably how I should have attempted it on the exam. Let’s use a hybrid coordinate vector and complex number representation to describe the particle position

$\begin{aligned}\mathbf{x}_c = \begin{bmatrix}a e^{i\theta} \\ h\end{bmatrix},\end{aligned} \hspace{\stretch{1}}(1.1)$

with the field measurement position of

$\begin{aligned}\mathbf{r} = \begin{bmatrix}\rho e^{i\phi} \\ z\end{bmatrix}.\end{aligned} \hspace{\stretch{1}}(1.2)$

The particle velocity is

$\begin{aligned}\mathbf{v}_c = \begin{bmatrix}(\dot{a} + i a \dot{\theta}) e^{i\theta} \\ \dot{h}\end{bmatrix} \\ =\begin{bmatrix}e^{i\theta} & i e^{i\theta} & 0 \\ 0 & 0 & 1\end{bmatrix} \begin{bmatrix}\dot{a} \\ a \dot{\theta} \\ \dot{h}\end{bmatrix}\end{aligned} \hspace{\stretch{1}}(1.3)$

We also want the vectorial difference between the field measurement position and the particle position

$\begin{aligned}\mathbf{R} = \mathbf{r} - \mathbf{x}_c = \begin{bmatrix}e^{i\phi} & -e^{i\theta} & 0 \\ 0 & 0 & 1\end{bmatrix}\begin{bmatrix}\rho \\ a \\ z - h\end{bmatrix}.\end{aligned} \hspace{\stretch{1}}(1.4)$

The dot product between $\mathbf{R}$ and $\mathbf{v}_c$ is then

$\begin{aligned}\mathbf{v}_c \cdot \mathbf{R} &=\begin{bmatrix}\dot{a} &a \dot{\theta} &\dot{h}\end{bmatrix}\text{Real} \left( \begin{bmatrix}e^{-i\theta} & 0 \\ -i e^{-i\theta} & 0 \\ 0 & 1\end{bmatrix} \begin{bmatrix}e^{i\phi} & -e^{i\theta} & 0 \\ 0 & 0 & 1\end{bmatrix}\right)\begin{bmatrix}\rho \\ a \\ z - h\end{bmatrix} \\ &=\begin{bmatrix}\dot{a} &a \dot{\theta} &\dot{h}\end{bmatrix}\text{Real} \left( \begin{bmatrix}e^{i(\phi - \theta)} & -1 & 0 \\ -i e^{i(\phi - \theta)} & i & 0 \\ 0 & 0 & 1\end{bmatrix} \right)\begin{bmatrix}\rho \\ a \\ z - h\end{bmatrix} \\ &=\begin{bmatrix}\dot{a} &a \dot{\theta} &\dot{h}\end{bmatrix}\begin{bmatrix}\cos(\phi - \theta) & -1 & 0 \\ \sin(\phi - \theta) & 0 & 0 \\ 0 & 0 & 1\end{bmatrix} \begin{bmatrix}\rho \\ a \\ z - h\end{bmatrix}.\end{aligned}$

Expansion of the final matrix products is then

$\begin{aligned}\mathbf{v}_c \cdot \mathbf{R} = \dot{h} (z - h) -a \dot{a} + \rho \dot{a} \cos(\phi- \theta) + \rho a^2 \dot{\theta} \sin(\phi - \theta)\end{aligned} \hspace{\stretch{1}}(1.5)$

The other quantity that we want is $\mathbf{R}^2$ , which is

$\begin{aligned}\mathbf{R}^2 &= \begin{bmatrix}\rho &a &(z - h)\end{bmatrix}\text{Real} \left(\begin{bmatrix}e^{-i\phi} & 0 \\ -e^{-i\theta} & 0 \\ 0 & 1\end{bmatrix}\begin{bmatrix}e^{i\phi} & -e^{i\theta} & 0 \\ 0 & 0 & 1\end{bmatrix}\right)\begin{bmatrix}\rho \\ a \\ z - h\end{bmatrix} \\ &=\begin{bmatrix}\rho &a &(z - h)\end{bmatrix}\begin{bmatrix}1 & -\cos(\phi-\theta) & 0 \\ -\cos(\phi-\theta) & 1 & 0 \\ 0 & 0 & 1\end{bmatrix} \begin{bmatrix}\rho \\ a \\ z - h\end{bmatrix} \\ \end{aligned}$

The retarded time at which the field is measured is therefore defined implicitly by

$\begin{aligned}R = \sqrt{(\rho^2 + (a(t_r))^2 + (z-h(t_r))^2 - 2 a(t_r) \rho \cos(\phi - \theta(t_r))} = c( t - t_r).\end{aligned} \hspace{\stretch{1}}(1.6)$

Together 1.3, 1.5, and 1.6 define the four potentials

$\begin{aligned}A^0 &= \frac{q}{R - \mathbf{R} \cdot \mathbf{v}_c/c} \\ \mathbf{A} &= \frac{\mathbf{v}_c}{c} A^0,\end{aligned} \hspace{\stretch{1}}(1.7)$

where all quantities are evaluated at the retarded time $t_r$ given by 1.6.

In the homework (and in the text [2] section 63) we found for $\mathbf{E}$ and $\mathbf{B}$

Expanding out the cross products this yields

$\begin{aligned}\mathbf{E} &= e (1 - \boldsymbol{\beta}_c^2) \frac{\hat{\mathbf{R}} - \boldsymbol{\beta}_c}{R^2 (1 - \hat{\mathbf{R}} \cdot \boldsymbol{\beta}_c)^3}+ e \frac{1}{R (1 - \hat{\mathbf{R}} \cdot \boldsymbol{\beta}_c)^3} (\hat{\mathbf{R}} - \boldsymbol{\beta}_c) \left(\hat{\mathbf{R}} \cdot \frac{\mathbf{a}_c}{c^2}\right)- e \frac{1}{R (1 - \hat{\mathbf{R}} \cdot \boldsymbol{\beta}_c)^2} \frac{\mathbf{a}_c}{c^2} \\ \mathbf{B} &= e (1 - \boldsymbol{\beta}_c^2) \frac{\boldsymbol{\beta}_c \times \hat{\mathbf{R}}}{R^2 (1 - \hat{\mathbf{R}} \cdot \boldsymbol{\beta}_c)^3}+ e \frac{1}{R (1 - \hat{\mathbf{R}} \cdot \boldsymbol{\beta}_c)^3} (\boldsymbol{\beta}_c \times \hat{\mathbf{R}}) \left(\hat{\mathbf{R}} \cdot \frac{\mathbf{a}_c}{c^2} \right)+ e \frac{1}{R (1 - \hat{\mathbf{R}} \cdot \boldsymbol{\beta}_c)^2} \frac{\mathbf{a}_c}{c^2} \times \hat{\mathbf{R}}\end{aligned} \hspace{\stretch{1}}(1.11)$

While longer, it is nice to call out the symmetry between $\mathbf{E}$ and $\mathbf{B}$ explicitly. As a side note, how do these combine in the Geometric Algebra formalism where we have $F = \mathbf{E} + I\mathbf{B}$ ? That gives us

$\begin{aligned}F = e \frac{1}{(1 - \hat{\mathbf{R}} \cdot \boldsymbol{\beta}_c)^3}\left(\left(\frac{1 - \boldsymbol{\beta}_c^2}{R^2} + \frac{\hat{\mathbf{R}} \cdot \mathbf{a}_c}{c R}\right)\left(\hat{\mathbf{R}} - \boldsymbol{\beta}_c + \hat{\mathbf{R}} \wedge (\hat{\mathbf{R}} - \boldsymbol{\beta}_c)\right)+ \frac{1}{{R}} \left( \frac{\mathbf{a}_c}{c^2}+ \frac{\mathbf{a}_c}{c^2} \wedge \hat{\mathbf{R}}\right)\right)\end{aligned} \hspace{\stretch{1}}(1.13)$

I’d guess a multivector of the form $\mathbf{a} + \mathbf{a} \wedge \hat{\mathbf{b}}$ , can be tidied up a bit more, but this won’t be persued here. Instead let’s write out the fields corresponding to the potentials of 1.7 explicitly. We need to calculate $\mathbf{a}_c$ , $\mathbf{v}_c \times \mathbf{R}$ , $\mathbf{a}_c \times \mathbf{R}$ , and $\mathbf{a}_c \cdot \mathbf{R}$ . For the acceleration we get

$\begin{aligned}\mathbf{a}_c =\begin{bmatrix}\left( \dot{d}{a} - a {\dot{\theta}}^2 + i ( a\dot{d}{\theta} + 2 \dot{a} \dot{\theta} ) \right) e^{i\theta} \\ \dot{d}{h}\end{bmatrix}\end{aligned} \hspace{\stretch{1}}(1.14)$

Dotted with $\mathbf{R}$ we have

$\begin{aligned}\mathbf{a}_c \cdot \mathbf{R}&=\begin{bmatrix}\left( \dot{d}{a} - a {\dot{\theta}}^2 + i ( a\dot{d}{\theta} + 2 \dot{a} \dot{\theta} ) \right) e^{i\theta} \\ \dot{d}{h}\end{bmatrix}\cdot \begin{bmatrix}\rho e^{i\phi} - a e^{i\theta} \\ h\end{bmatrix} \\ &=h \dot{d}{h} + \text{Real}\left( \left( \dot{d}{a} - a {\dot{\theta}}^2 + i ( a\dot{d}{\theta} + 2 \dot{a} \dot{\theta} ) \right) \left(\rho e^{i(\theta- \phi)} - a\right)\right) ,\end{aligned}$

which gives us

$\begin{aligned}\mathbf{a}_c \cdot \mathbf{R} =h \dot{d}{h} + ( \dot{d}{a} - a {\dot{\theta}}^2 ) (\rho \cos(\phi - \theta) - a)+ (a \dot{d}{\theta} + 2 \dot{a} \dot{\theta}) \rho \sin(\phi - \theta).\end{aligned} \hspace{\stretch{1}}(1.15)$

Now, how do we handle the cross products in this complex number, scalar hybrid format? With some playing around such a cross product can be put into the following tidy form

$\begin{aligned}\begin{bmatrix}z_1 \\ h_1\end{bmatrix}\times\begin{bmatrix}z_2 \\ h_2\end{bmatrix}= \begin{bmatrix}i (h_1 z_2 - h_2 z_1) \\ \text{Imag}(z_1^{*} z_2)\end{bmatrix}.\end{aligned} \hspace{\stretch{1}}(1.16)$

This is a sensible result. Crossing with $\mathbf{e}_3$ will rotate in the $x-y$ plane, which accounts for the factors of $i$ in the complex portion of the cross product. The imaginary part has only contributions from the portions of the vectors $z_1$ and $z_2$ that are perpendicular to each other, so while the real part of $z_1^{*} z_2$ measures the colinearity, the imaginary part is a measure of the amount perpendicular.

Using this for our velocity cross product we have

$\begin{aligned}\mathbf{v}_c \times \mathbf{R} &=\begin{bmatrix}(\dot{a} + i a \dot{\theta}) e^{i\theta} \\ \dot{h}\end{bmatrix}\times\begin{bmatrix}\rho e^{i\phi} - a e^{i\theta} \\ h\end{bmatrix} \\ &=\begin{bmatrix}i\left(\dot{h} ( \rho e^{i\phi} - a e^{i\theta} ) - h (\dot{a} + i a \dot{\theta}) e^{i\theta} \right) \\ \text{Imag} \left( ( \dot{a} - i a \dot{\theta}) (\rho e^{i(\phi - \theta)} - a) \right)\end{bmatrix} \end{aligned}$

which is

$\begin{aligned}\mathbf{v}_c \times \mathbf{R} =\begin{bmatrix}i( \dot{h} \rho e^{i\phi} - (h \dot{a} + i h a \dot{\theta} + a \dot{h}) e^{i\theta} ) \\ \dot{a} \rho \sin(\phi - \theta) - a \dot{\theta} \rho \cos(\phi - \theta) + a^2 \dot{\theta}\end{bmatrix}.\end{aligned} \hspace{\stretch{1}}(1.17)$

The last thing required to write out the fields is

$\begin{aligned}\mathbf{a}_c \times \mathbf{R} &=\begin{bmatrix}\left( \dot{d}{a} - a {\dot{\theta}}^2 + i ( a\dot{d}{\theta} + 2 \dot{a} \dot{\theta} ) \right) e^{i\theta} \\ \dot{d}{h}\end{bmatrix}\times\begin{bmatrix}\rho e^{i\phi} - a e^{i\theta} \\ z - h\end{bmatrix} \\ &=\begin{bmatrix}i \dot{d}{h} (\rho e^{i\phi} - a e^{i\theta} ) - i (z - h) \left( \dot{d}{a} - a {\dot{\theta}}^2 + i ( a\dot{d}{\theta} + 2 \dot{a} \dot{\theta} ) \right) e^{i\theta} \\ \text{Imag} \left( \left( \dot{d}{a} - a {\dot{\theta}}^2 - i ( a\dot{d}{\theta} + 2 \dot{a} \dot{\theta} ) \right) ( \rho e^{i(\phi -\theta)} - a )\right)\end{bmatrix} \\ \end{aligned}$

So the acceleration cross product is

$\begin{aligned}\mathbf{a}_c \times \mathbf{R} =\begin{bmatrix}i \dot{d}{h} \rho e^{i\phi} - i \left( \dot{d}{h} a + (z - h) \left( \dot{d}{a} - a {\dot{\theta}}^2 + i ( a\dot{d}{\theta} + 2 \dot{a} \dot{\theta} ) \right) \right) e^{i\theta} \\ \left( \dot{d}{a} - a {\dot{\theta}}^2 \right) \rho \sin(\phi - \theta)-( a\dot{d}{\theta} + 2 \dot{a} \dot{\theta} ) (\rho \cos(\phi -\theta) - a)\end{bmatrix}\end{aligned} \hspace{\stretch{1}}(1.18)$

Putting all the results together creates something that is too long to easily write, but can at least be summarized

$\begin{aligned}\mathbf{E} &= \frac{e}{(R - \mathbf{R} \cdot \boldsymbol{\beta}_c)^3}\left(\left(1 - \boldsymbol{\beta}_c^2 + \mathbf{R} \cdot \frac{\mathbf{a}_c}{c^2}\right) (\mathbf{R} - \boldsymbol{\beta}_c R)- R(R - \mathbf{R} \cdot \boldsymbol{\beta}_c) \frac{\mathbf{a}_c}{c^2} \right) \\ \mathbf{B} &= \frac{e}{(R - \mathbf{R} \cdot \boldsymbol{\beta}_c)^3}\left(\left(1 - \boldsymbol{\beta}_c^2 + \mathbf{R} \cdot \frac{\mathbf{a}_c}{c^2}\right) (\boldsymbol{\beta}_c \times \mathbf{R})- (R - \mathbf{R} \cdot \boldsymbol{\beta}_c) \frac{\mathbf{a}_c}{c^2} \times \mathbf{R}\right) \\ 1 - \boldsymbol{\beta}_c^2 &= 1 - (\dot{a}^2 + a^2 \dot{\theta}^2 + \dot{h}^2)/c^2 \\ R &= \sqrt{(\rho^2 + (a(t_r))^2 + (z-h(t_r))^2 - 2 a(t_r) \rho \cos(\phi - \theta(t_r))} = c( t - t_r) \\ \mathbf{R} - \boldsymbol{\beta}_c R &= \begin{bmatrix}\rho e^{i\phi} - (a + (\dot{a} + i a\dot{\theta}) R/c) e^{i\theta} \\ z - h - \dot{h} R/c\end{bmatrix} \\ \boldsymbol{\beta}_c \cdot \mathbf{R} &= \frac{1}{{c}}\left( \dot{h} (z - h) -a \dot{a} + \rho \dot{a} \cos(\phi- \theta) + \rho a^2 \dot{\theta} \sin(\phi - \theta) \right) \\ \boldsymbol{\beta}_c \times \mathbf{R} &=\frac{1}{{c}}\begin{bmatrix}i( \dot{h} \rho e^{i\phi} - (h \dot{a} + i h a \dot{\theta} + a \dot{h}) e^{i\theta} ) \\ \dot{a} \rho \sin(\phi - \theta) - a \dot{\theta} \rho \cos(\phi - \theta) + a^2 \dot{\theta}\end{bmatrix} \\ \frac{\mathbf{a}_c}{c^2} &=\frac{1}{{c^2}}\begin{bmatrix}\left( \dot{d}{a} - a {\dot{\theta}}^2 + i ( a\dot{d}{\theta} + 2 \dot{a} \dot{\theta} ) \right) e^{i\theta} \\ \dot{d}{h}\end{bmatrix} \\ \frac{\mathbf{a}_c}{c^2} \cdot \mathbf{R} &=\frac{1}{{c^2}} \left(h \dot{d}{h} + ( \dot{d}{a} - a {\dot{\theta}}^2 ) (\rho \cos(\phi - \theta) - a)+ (a \dot{d}{\theta} + 2 \dot{a} \dot{\theta}) \rho \sin(\phi - \theta) \right) \\ \frac{\mathbf{a}_c}{c^2} \times \mathbf{R} &=\frac{1}{{c^2}}\begin{bmatrix}i \dot{d}{h} \rho e^{i\phi} - i \left( \dot{d}{h} a + (z - h) \left( \dot{d}{a} - a {\dot{\theta}}^2 + i ( a\dot{d}{\theta} + 2 \dot{a} \dot{\theta} ) \right) \right) e^{i\theta} \\ \left( \dot{d}{a} - a {\dot{\theta}}^2 \right) \rho \sin(\phi - \theta)-( a\dot{d}{\theta} + 2 \dot{a} \dot{\theta} ) (\rho \cos(\phi -\theta) - a)\end{bmatrix}.\end{aligned} \hspace{\stretch{1}}(1.19)$

This is a whole lot more than the exam question asked for, since it is actually the most general solution to the electric and magnetic fields associated with an arbitrary charged particle (when that motion is described in cylindrical coordinates). The exam question had $\theta = k c t$ and $\dot{a} = 0, h = 0$ , which kills a number of the terms

$\begin{aligned}1 - \boldsymbol{\beta}_c^2 + \frac{\mathbf{a}_c}{c^2} \cdot \mathbf{R} &= 1 - a k^2 \rho \cos(\phi - k c t_r) \\ R &= \sqrt{(\rho^2 + a^2 + z^2 - 2 a \rho \cos(\phi - k c t_r)} = c( t - t_r) \\ \mathbf{R} - \boldsymbol{\beta}_c R &= \begin{bmatrix}\rho e^{i\phi} - a (1 + i k R) e^{i k c t_r} \\ z \end{bmatrix} \\ \boldsymbol{\beta}_c \cdot \mathbf{R} &= \rho a^2 k \sin(\phi - k c t_r) \\ \boldsymbol{\beta}_c \times \mathbf{R} &=\begin{bmatrix}0 \\ a k ( a - \rho \cos(\phi - k c t_r) )\end{bmatrix} \\ \frac{\mathbf{a}_c}{c^2} &=\begin{bmatrix}- a k^2 e^{i k c t_r} \\ 0\end{bmatrix} \\ \frac{\mathbf{a}_c}{c^2} \times \mathbf{R} &=\begin{bmatrix}i z a k^2 e^{i k c t_r} \\ - a k^2 \rho \sin(\phi - k c t_r)\end{bmatrix}.\end{aligned} \hspace{\stretch{1}}(1.29)$

This is still messy, but is a satisfactory solution to the problem.

The exam question also asked only about the $\rho = 0$ , so $\phi$ also becomes irrelevant. In that case we have along the z-axis the fields are given by

$\begin{aligned}\mathbf{E}(z)&= \frac{e}{R^3}\begin{bmatrix}- a (1 + i k R - k^2 R^2 ) e^{i k (c t - R)} \\ z \end{bmatrix} \\ \mathbf{B}(z)&= \frac{e}{R^3}\begin{bmatrix}-R i z a k^2 e^{i k (c t - R)} \\ a^2 k \end{bmatrix} \\ R &= \sqrt{a^2 + z^2} \end{aligned} \hspace{\stretch{1}}(1.36)$

Similar to when things were calculated from the potentials directly, I get a different result from $\hat{\mathbf{R}} \times \mathbf{E}$

$\begin{aligned}\hat{\mathbf{R}} \times \mathbf{E}(z) = \frac{e}{R^3}\begin{bmatrix}a k z (1 + i k R) e^{i k (c t - R)} \\ -a^2 k \end{bmatrix}\end{aligned} \hspace{\stretch{1}}(1.39)$

compared to the value of $\mathbf{B}$ that was directly calculated above. With the sign swapped in the z-axis term of $\mathbf{B}(z)$ here I’d guess I’ve got an algebraic error hiding somewhere?

References

[1] Peeter Joot. {A cylindrical Lienard-Wiechert potential calculation using multivector matrix products.} [online]. http://sites.google.com/site/peeterjoot/math2011/matrixVectorPotentials.pdf.

[2] L.D. Landau and E.M. Lifshitz. The classical theory of fields. Butterworth-Heinemann, 1980.

Posted in Math and Physics Learning. | Tagged: circular motion, complex cylindrical coordinates, Lienard-Wiechert potentials, PHY450, retarded time | Leave a Comment »

My first arxiv submission. Change of basis and Gram-Schmidt orthonormalization in special relativity

Posted by peeterjoot on April 29, 2011

Now that I have an academic email address I was able to make an arxiv submission (I’d tried previously and been auto-rejected) :

Change of basis and Gram-Schmidt orthonormalization in special relativity

This is based on a tutorial from our relativistic electrodynamics class, which covered non-internal relativistic systems. Combining what I learned from that with some concepts I learned from ‘Geometric Algebra for Physicists’ (particularly reciprocal frames) I was able to write up some notes that took those ideas plus basic linear algebra (the Graham-Schmidt procedure) and apply them to relativity and/or non-orthonormal Euclidean bases. How to do projections onto non-orthonormal Euclidean bases isn’t taught in Algebra I, but once you figure out that the same thing works for SR.

Will anybody read it? I don’t know … but I had fun writing it.

Posted in Math and Physics Learning. | Tagged: change of basis, dual vector, Gram-Schmidt orthonormalization, inertial frame, lorentz boost, PHY450, reciprocal basis, special relativity | 2 Comments »

PHY450HS1: Relativistic electrodynamics: some exam reflection.

Posted by peeterjoot on April 28, 2011

[Click here for a PDF of this post with nicer formatting (especially if my latex to wordpress script has left FORMULA DOES NOT PARSE errors.)]

Charged particle in a circle.

From the 2008 PHY353 exam, given a particle of charge $q$ moving in a circle of radius $a$ at constant angular frequency 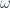$\omega$ .

\begin{itemize}
\item Find the Lienard-Wiechert potentials for points on the z-axis.
\item Find the electric and magnetic fields at the center.
\end{itemize}

When I tried this I did it for points not just on the z-axis. It turns out that we also got this question on the exam (but stated slightly differently). Since I’ll not get to see my exam solution again, let’s work through this at a leisurely rate, and see if things look right. The problem as stated in this old practice exam is easier since it doesn’t say to calculate the fields from the four potentials, so there was nothing preventing one from just grinding away and plugging stuff into the Lienard-Wiechert equations for the fields (as I did when I tried it for practice).

The potentials.

Let’s set up our coordinate system in cylindrical coordinates. For the charged particle and the point that we measure the field, with $i = \mathbf{e}_1 \mathbf{e}_2$

$\begin{aligned}\mathbf{x}(t) &= a \mathbf{e}_1 e^{i \omega t} \\ \mathbf{r} &= z \mathbf{e}_3 + \rho \mathbf{e}_1 e^{i \phi}\end{aligned} \hspace{\stretch{1}}(1.1)$

Here I’m using the geometric product of vectors (if that’s unfamiliar then just substitute

$\begin{aligned}\{\mathbf{e}_1, \mathbf{e}_2, \mathbf{e}_3\} \rightarrow \{\sigma_1, \sigma_2, \sigma_3\}\end{aligned} \hspace{\stretch{1}}(1.3)$

We can do that since the Pauli matrices also have the same semantics (with a small difference since the geometric square of a unit vector is defined as the unit scalar, whereas the Pauli matrix square is the identity matrix). The semantics we require of this vector product are just 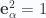$\mathbf{e}_\alpha^2 = 1$ and $\mathbf{e}_\alpha \mathbf{e}_\beta = - \mathbf{e}_\beta \mathbf{e}_\alpha$ for any $\alpha \ne \beta$ .

I’ll also be loose with notation and use 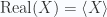$\text{Real}(X) = \left\langle{{X}}\right\rangle$ to select the scalar part of a multivector (or with the Pauli matrices, the portion proportional to the identity matrix).

Our task is to compute the Lienard-Wiechert potentials. Those are

$\begin{aligned}A^0 &= \frac{q}{R^{*}} \\ \mathbf{A} &= A^0 \frac{\mathbf{v}}{c},\end{aligned} \hspace{\stretch{1}}(1.4)$

where

$\begin{aligned}\mathbf{R} &= \mathbf{r} - \mathbf{x}(t_r) \\ R = {\left\lvert{\mathbf{R}}\right\rvert} &= c (t - t_r) \\ R^{*} &= R - \frac{\mathbf{v}}{c} \cdot \mathbf{R} \\ \mathbf{v} &= \frac{d\mathbf{x}}{dt_r}.\end{aligned} \hspace{\stretch{1}}(1.6)$

We’ll need (eventually)

$\begin{aligned}\mathbf{v} &= a \omega \mathbf{e}_2 e^{i \omega t_r} = a \omega ( -\sin \omega t_r, \cos\omega t_r, 0) \\ \dot{\mathbf{v}} &= -a \omega^2 \mathbf{e}_1 e^{i \omega t_r} = -a \omega^2 (\cos\omega t_r, \sin\omega t_r, 0)\end{aligned} \hspace{\stretch{1}}(1.10)$

and also need our retarded distance vector

$\begin{aligned}\mathbf{R} = z \mathbf{e}_3 + \mathbf{e}_1 (\rho e^{i \phi} - a e^{i \omega t_r} ),\end{aligned} \hspace{\stretch{1}}(1.12)$

From this we have

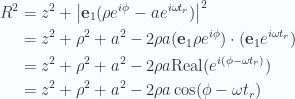
$\begin{aligned}R^2 &= z^2 + {\left\lvert{\mathbf{e}_1 (\rho e^{i \phi} - a e^{i \omega t_r} )}\right\rvert}^2 \\ &= z^2 + \rho^2 + a^2 - 2 \rho a (\mathbf{e}_1 \rho e^{i \phi}) \cdot (\mathbf{e}_1 e^{i \omega t_r}) \\ &= z^2 + \rho^2 + a^2 - 2 \rho a \text{Real}( e^{ i(\phi - \omega t_r) } ) \\ &= z^2 + \rho^2 + a^2 - 2 \rho a \cos(\phi - \omega t_r)\end{aligned}$

$\begin{aligned}R = \sqrt{z^2 + \rho^2 + a^2 - 2 \rho a \cos( \phi - \omega t_r ) }.\end{aligned} \hspace{\stretch{1}}(1.13)$

Next we need

$\begin{aligned}\mathbf{R} \cdot \mathbf{v}/c&= (z \mathbf{e}_3 + \mathbf{e}_1 (\rho e^{i \phi} - a e^{i \omega t_r} )) \cdot \left(a \frac{\omega}{c} \mathbf{e}_2 e^{i \omega t_r} \right) \\ &=a \frac{\omega }{c}\text{Real}(i (\rho e^{-i \phi} - a e^{-i \omega t_r} ) e^{i \omega t_r} ) \\ &=a \frac{\omega }{c}\rho \text{Real}( i e^{-i \phi + i \omega t_r} ) \\ &=a \frac{\omega }{c}\rho \sin(\phi - \omega t_r)\end{aligned}$

So we have

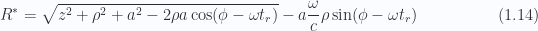
$\begin{aligned}R^{*} = \sqrt{z^2 + \rho^2 + a^2 - 2 \rho a \cos( \phi - \omega t_r ) }-a \frac{\omega }{c} \rho \sin(\phi - \omega t_r)\end{aligned} \hspace{\stretch{1}}(1.14)$

Writing 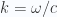$k = \omega/c$ , and having a peek back at 1.4, our potentials are now solved for

$\begin{aligned}\boxed{\begin{aligned}A^0 &= \frac{q}{\sqrt{z^2 + \rho^2 + a^2 - 2 \rho a \cos( \phi - k c t_r ) }} \\ \mathbf{A} &= A^0 a k ( -\sin k c t_r, \cos k c t_r, 0).\end{aligned}}\end{aligned} \hspace{\stretch{1}}(1.24)$

The caveat is that 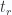$t_r$ is only specified implicitly, according to

$\begin{aligned}\boxed{c t_r = c t - \sqrt{z^2 + \rho^2 + a^2 - 2 \rho a \cos( \phi - k c t_r ) }.}\end{aligned} \hspace{\stretch{1}}(1.16)$

There doesn’t appear to be much hope of solving for 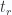$t_r$ explicitly in closed form.

General fields for this system.

With

$\begin{aligned}\mathbf{R}^{*} = \mathbf{R} - \frac{\mathbf{v}}{c} R,\end{aligned} \hspace{\stretch{1}}(1.17)$

the fields are

$\begin{aligned}\boxed{\begin{aligned}\mathbf{E} &= q (1 - \mathbf{v}^2/c^2) \frac{\mathbf{R}^{*}}{{R^{*}}^3} + \frac{q}{{R^{*}}^3} \mathbf{R} \times (\mathbf{R}^{*} \times \dot{\mathbf{v}}/c^2) \\ \mathbf{B} &= \frac{\mathbf{R}}{R} \times \mathbf{E}.\end{aligned}}\end{aligned} \hspace{\stretch{1}}(1.18)$

In there we have

$\begin{aligned}1 - \mathbf{v}^2/c^2 = 1 - a^2 \frac{\omega^2}{c^2} = 1 - a^2 k^2\end{aligned} \hspace{\stretch{1}}(1.19)$

and

$\begin{aligned}\mathbf{R}^{*} &= z \mathbf{e}_3 + \mathbf{e}_1 (\rho e^{i \phi} - a e^{i k c t_r} )-a k \mathbf{e}_2 e^{i k c t_r} R \\ &= z \mathbf{e}_3 + \mathbf{e}_1 (\rho e^{i \phi} - a (1 - k R i) e^{i k c t_r} )\end{aligned}$

Writing this out in coordinates isn’t particularly illuminating, but can be done for completeness without too much trouble

$\begin{aligned}\mathbf{R}^{*} = ( \rho \cos\phi - a \cos t_r + a k R \sin t_r, \rho \sin\phi - a \sin t_r - a k R \cos t_r, z )\end{aligned} \hspace{\stretch{1}}(1.20)$

In one sense the problem could be considered solved, since we have all the pieces of the puzzle. The outstanding question is whether or not the resulting mess can be simplified at all. Let’s see if the cross product reduces at all. Using

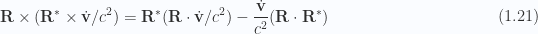
$\begin{aligned}\mathbf{R} \times (\mathbf{R}^{*} \times \dot{\mathbf{v}}/c^2) =\mathbf{R}^{*} (\mathbf{R} \cdot \dot{\mathbf{v}}/c^2) - \frac{\dot{\mathbf{v}}}{c^2}(\mathbf{R} \cdot \mathbf{R}^{*})\end{aligned} \hspace{\stretch{1}}(1.21)$

Perhaps one or more of these dot products can be simplified? One of them does reduce nicely

$\begin{aligned}\mathbf{R}^{*} \cdot \mathbf{R} &= ( \mathbf{R} - R \mathbf{v}/c ) \cdot \mathbf{R} \\ &= R^2 - (\mathbf{R} \cdot \mathbf{v}/c) R \\ &= R^2 - R a k \rho \sin(\phi - k c t_r) \\ &= R(R - a k \rho \sin(\phi - k c t_r))\end{aligned}$

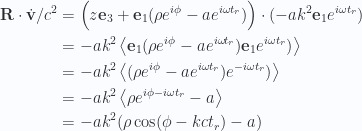
$\begin{aligned}\mathbf{R} \cdot \dot{\mathbf{v}}/c^2&=\Bigl(z \mathbf{e}_3 + \mathbf{e}_1 (\rho e^{i \phi} - a e^{i \omega t_r} ) \Bigr) \cdot(-a k^2 \mathbf{e}_1 e^{i \omega t_r} ) \\ &=- a k^2 \left\langle{{\mathbf{e}_1 (\rho e^{i \phi} - a e^{i \omega t_r} ) \mathbf{e}_1 e^{i \omega t_r} ) }}\right\rangle \\ &=- a k^2 \left\langle{{(\rho e^{i \phi} - a e^{i \omega t_r} ) e^{-i \omega t_r} ) }}\right\rangle \\ &=- a k^2 \left\langle{{\rho e^{i \phi - i \omega t_r} - a }}\right\rangle \\ &=- a k^2 ( \rho \cos(\phi - k c t_r) - a )\end{aligned}$

Putting this cross product back together we have

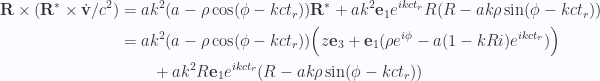
$\begin{aligned}\mathbf{R} \times (\mathbf{R}^{*} \times \dot{\mathbf{v}}/c^2)&=a k^2 ( a -\rho \cos(\phi - k c t_r) ) \mathbf{R}^{*} +a k^2 \mathbf{e}_1 e^{i k c t_r} R(R - a k \rho \sin(\phi - k c t_r)) \\ &=a k^2 ( a -\rho \cos(\phi - k c t_r) ) \Bigl(z \mathbf{e}_3 + \mathbf{e}_1 (\rho e^{i \phi} - a (1 - k R i) e^{i k c t_r} )\Bigr) \\ &\qquad +a k^2 R \mathbf{e}_1 e^{i k c t_r} (R - a k \rho \sin(\phi - k c t_r)) \end{aligned}$

Writing

$\begin{aligned}\phi_r = \phi - k c t_r,\end{aligned} \hspace{\stretch{1}}(1.22)$

this can be grouped into similar terms

$\begin{aligned}\begin{aligned}\mathbf{R} \times (\mathbf{R}^{*} \times \dot{\mathbf{v}}/c^2)&=a k^2 (a - \rho \cos\phi_r) z \mathbf{e}_3 \\ &+ a k^2 \mathbf{e}_1(a - \rho \cos\phi_r) \rho e^{i\phi} \\ &+ a k^2 \mathbf{e}_1\left(-a (a - \rho \cos\phi_r) (1 - k R i)+ R(R - a k \rho \sin \phi_r)\right) e^{i k c t_r}\end{aligned}\end{aligned} \hspace{\stretch{1}}(1.23)$

The electric field pieces can now be collected. Not expanding out the $R^{*}$ from 1.14, this is

$\begin{aligned}\begin{aligned}\mathbf{E} &= \frac{q}{(R^{*})^3} z \mathbf{e}_3\Bigl( 1 - a \rho k^2 \cos\phi_r \Bigr) \\ &+\frac{q}{(R^{*})^3} \rho\mathbf{e}_1 \Bigl(1 - a \rho k^2 \cos\phi_r \Bigr) e^{i\phi} \\ &+\frac{q}{(R^{*})^3} a \mathbf{e}_1\left(-\Bigl( 1 + a k^2 (a - \rho \cos\phi_r) \Bigr) (1 - k R i)(1 - a^2 k^2)+ k^2 R(R - a k \rho \sin \phi_r)\right) e^{i k c t_r}\end{aligned}\end{aligned} \hspace{\stretch{1}}(1.24)$

Along the z-axis where $\rho = 0$ what do we have?

$\begin{aligned}R = \sqrt{z^2 + a^2 } \end{aligned} \hspace{\stretch{1}}(1.25)$

$\begin{aligned}A^0 = \frac{q}{R} \end{aligned} \hspace{\stretch{1}}(1.26)$

$\begin{aligned}\mathbf{A} = A^0 a k \mathbf{e}_2 e^{i k c t_r } \end{aligned} \hspace{\stretch{1}}(1.27)$

$\begin{aligned}c t_r = c t - \sqrt{z^2 + a^2 } \end{aligned} \hspace{\stretch{1}}(1.28)$

$\begin{aligned}\begin{aligned}\mathbf{E} &= \frac{q}{R^3} z \mathbf{e}_3 \\ &+\frac{q}{R^3} a \mathbf{e}_1\left(-( 1 - a^4 k^4 ) (1 - k R i)+ k^2 R^2 \right) e^{i k c t_r} \end{aligned}\end{aligned} \hspace{\stretch{1}}(1.29)$

$\begin{aligned}\mathbf{B} = \frac{ z \mathbf{e}_3 - a \mathbf{e}_1 e^{i k c t_r}}{R} \times \mathbf{E}\end{aligned} \hspace{\stretch{1}}(1.30)$

The magnetic term here looks like it can be reduced a bit.

An approximation near the center.

Unlike the old exam I did, where it didn’t specify that the potentials had to be used to calculate the fields, and the problem was reduced to one of algebraic manipulation, our exam explicitly asked for the potentials to be used to calculate the fields.

There was also the restriction to compute them near the center. Setting $\rho = 0$ so that we are looking only near the z-axis, we have

$\begin{aligned}A^0 &= \frac{q}{\sqrt{z^2 + a^2}} \\ \mathbf{A} &= \frac{q a k \mathbf{e}_2 e^{i k c t_r} }{\sqrt{z^2 + a^2}} = \frac{q a k (-\sin k c t_r, \cos k c t_r, 0)}{\sqrt{z^2 + a^2}} \\ t_r &= t - R/c = t - \sqrt{z^2 + a^2}/c\end{aligned} \hspace{\stretch{1}}(1.31)$

Now we are set to calculate the electric and magnetic fields directly from these. Observe that we have a spatial dependence in due to the 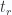$t_r$ quantities and that will have an effect when we operate with the gradient.

In the exam I’d asked Simon (our TA) if this question was asking for the fields at the origin (ie: in the plane of the charge’s motion in the center) or along the z-axis. He said in the plane. That would simplify things, but perhaps too much since $A^0$ becomes constant (in my exam attempt I somehow fudged this to get what I wanted for the $v = 0$ case, but that must have been wrong, and was the result of rushed work).

Let’s now proceed with the field calculation from these potentials

$\begin{aligned}\mathbf{E} &= - \boldsymbol{\nabla} A^0 - \frac{1}{{c}} \frac{\partial {\mathbf{A}}}{\partial {t}} \\ \mathbf{B} &= \boldsymbol{\nabla} \times \mathbf{A}.\end{aligned} \hspace{\stretch{1}}(1.34)$

For the electric field we need

$\begin{aligned}\boldsymbol{\nabla} A^0 &= q \mathbf{e}_3 \partial_z (z^2 + a^2)^{-1/2} \\ &= -q \mathbf{e}_3 \frac{z}{(\sqrt{z^2 + a^2})^3},\end{aligned}$

and

$\begin{aligned}\frac{1}{{c}} \frac{\partial {\mathbf{A}}}{\partial {t}} =\frac{q a k^2 \mathbf{e}_2 \mathbf{e}_1 \mathbf{e}_2 e^{i k c t_r} }{\sqrt{z^2 + a^2}}.\end{aligned} \hspace{\stretch{1}}(1.36)$

Putting these together, our electric field near the z-axis is

$\begin{aligned}\mathbf{E} = q \mathbf{e}_3 \frac{z}{(\sqrt{z^2 + a^2})^3}+\frac{q a k^2 \mathbf{e}_1 e^{i k c t_r} }{\sqrt{z^2 + a^2}}.\end{aligned} \hspace{\stretch{1}}(1.37)$

(another mistake I made on the exam, since I somehow fooled myself into forcing what I knew had to be in the gradient term, despite having essentially a constant scalar potential (having taken 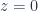$z = 0$ )).

What do we get for the magnetic field. In that case we have

$\begin{aligned}\boldsymbol{\nabla} \times \mathbf{A}(z)&=\mathbf{e}_\alpha \times \partial_\alpha \mathbf{A} \\ &=\mathbf{e}_3 \times \partial_z \frac{q a k \mathbf{e}_2 e^{i k c t_r} }{\sqrt{z^2 + a^2}} \\ &=\mathbf{e}_3 \times (\mathbf{e}_2 e^{i k c t_r} ) q a k \frac{\partial {}}{\partial {z}} \frac{1}{{\sqrt{z^2 + a^2}}} +q a k \frac{1}{{\sqrt{z^2 + a^2}}} \mathbf{e}_3 \times (\mathbf{e}_2 \partial_z e^{i k c t_r} ) \\ &=-\mathbf{e}_3 \times (\mathbf{e}_2 e^{i k c t_r} ) q a k \frac{z}{(\sqrt{z^2 + a^2})^3} +q a k \frac{1}{{\sqrt{z^2 + a^2}}} \mathbf{e}_3 \times \left( \mathbf{e}_2 \mathbf{e}_1 \mathbf{e}_2 k c e^{i k c t_r} \partial_z ( t - \sqrt{z^a + a^2}/c ) \right) \\ &=-\mathbf{e}_3 \times (\mathbf{e}_2 e^{i k c t_r} ) q a k \frac{z}{(\sqrt{z^2 + a^2})^3} -q a k^2 \frac{z}{z^2 + a^2} \mathbf{e}_3 \times \left( \mathbf{e}_1 k e^{i k c t_r} \right) \\ &=-\frac{q a k z \mathbf{e}_3}{z^2 + a^2} \times \left( \frac{ \mathbf{e}_2 e^{i k c t_r} }{\sqrt{z^2 + a^2}} + k \mathbf{e}_1 e^{i k c t_r} \right)\end{aligned}$

For the direction vectors in the cross products above we have

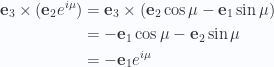
$\begin{aligned}\mathbf{e}_3 \times (\mathbf{e}_2 e^{i \mu})&=\mathbf{e}_3 \times (\mathbf{e}_2 \cos\mu - \mathbf{e}_1 \sin\mu) \\ &=-\mathbf{e}_1 \cos\mu - \mathbf{e}_2 \sin\mu \\ &=-\mathbf{e}_1 e^{i \mu}\end{aligned}$

and

$\begin{aligned}\mathbf{e}_3 \times (\mathbf{e}_1 e^{i \mu})&=\mathbf{e}_3 \times (\mathbf{e}_1 \cos\mu + \mathbf{e}_2 \sin\mu) \\ &=\mathbf{e}_2 \cos\mu - \mathbf{e}_1 \sin\mu \\ &=\mathbf{e}_2 e^{i \mu}\end{aligned}$

Putting everything, and summarizing results for the fields, we have

$\begin{aligned}\mathbf{E} &= q \mathbf{e}_3 \frac{z}{(\sqrt{z^2 + a^2})^3}+\frac{q a k^2 \mathbf{e}_1 e^{i \omega t_r} }{\sqrt{z^2 + a^2}} \\ \mathbf{B} &= \frac{q a k z}{ z^2 + a^2} \left( \frac{\mathbf{e}_1}{\sqrt{z^2 + a^2}} - k \mathbf{e}_2 \right) e^{i \omega t_r}\end{aligned} \hspace{\stretch{1}}(1.38)$

The electric field expression above compares well to 1.29. We have the Coulomb term and the radiation term. It is harder to compare the magnetic field to the exact result 1.30 since I did not expand that out.

FIXME: A question to consider. If all this worked should we not also get

$\begin{aligned}\mathbf{B} \stackrel{?}{=}\frac{z \mathbf{e}_3 - \mathbf{e}_1 a e^{i \omega t_r}}{\sqrt{z^2 + a^2}} \times \mathbf{E}.\end{aligned} \hspace{\stretch{1}}(1.40)$

However, if I do this check I get

$\begin{aligned}\mathbf{B} =\frac{q a z}{z^2 + a^2} \left( \frac{1}{{z^2 + a^2}} + k^2 \right) \mathbf{e}_2 e^{i \omega t_r}.\end{aligned} \hspace{\stretch{1}}(1.41)$

Collision of photon and electron.

I made a dumb error on the exam on this one. I setup the four momentum conservation statement, but then didn’t multiply out the cross terms properly. This led me to incorrectly assume that I had to try doing this the hard way (something akin to what I did on the midterm). Simon later told us in the tutorial the simple way, and that’s all we needed here too. Here’s the setup.

An electron at rest initially has four momentum

$\begin{aligned}(m c, 0)\end{aligned} \hspace{\stretch{1}}(2.42)$

where the incoming photon has four momentum

$\begin{aligned}\left(\hbar \frac{\omega}{c}, \hbar \mathbf{k} \right)\end{aligned} \hspace{\stretch{1}}(2.43)$

After the collision our electron has some velocity so its four momentum becomes (say)

$\begin{aligned}\gamma (m c, m \mathbf{v}),\end{aligned} \hspace{\stretch{1}}(2.44)$

and our new photon, going off on an angle $\theta$ relative to $\mathbf{k}$ has four momentum

$\begin{aligned}\left(\hbar \frac{\omega'}{c}, \hbar \mathbf{k}' \right)\end{aligned} \hspace{\stretch{1}}(2.45)$

Our conservation relationship is thus

$\begin{aligned}(m c, 0) + \left(\hbar \frac{\omega}{c}, \hbar \mathbf{k} \right)=\gamma (m c, m \mathbf{v})+\left(\hbar \frac{\omega'}{c}, \hbar \mathbf{k}' \right)\end{aligned} \hspace{\stretch{1}}(2.46)$

I squared both sides, but dropped my cross terms, which was just plain wrong, and costly for both time and effort on the exam. What I should have done was just

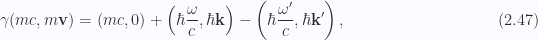
$\begin{aligned}\gamma (m c, m \mathbf{v}) =(m c, 0) + \left(\hbar \frac{\omega}{c}, \hbar \mathbf{k} \right)-\left(\hbar \frac{\omega'}{c}, \hbar \mathbf{k}' \right),\end{aligned} \hspace{\stretch{1}}(2.47)$

and then square this (really making contractions of the form $p_i p^i$ ). That gives (and this time keeping my cross terms)

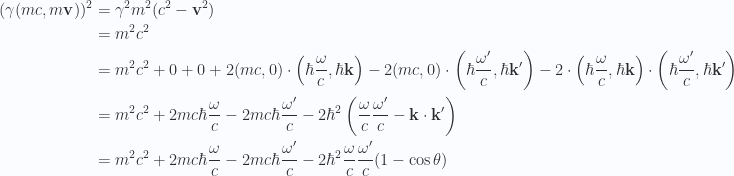
$\begin{aligned}(\gamma (m c, m \mathbf{v}) )^2 &= \gamma^2 m^2 (c^2 - \mathbf{v}^2) \\ &= m^2 c^2 \\ &=m^2 c^2 + 0 + 0+ 2 (m c, 0) \cdot \left(\hbar \frac{\omega}{c}, \hbar \mathbf{k} \right)- 2 (m c, 0) \cdot \left(\hbar \frac{\omega'}{c}, \hbar \mathbf{k}' \right)- 2 \cdot \left(\hbar \frac{\omega}{c}, \hbar \mathbf{k} \right)\cdot \left(\hbar \frac{\omega'}{c}, \hbar \mathbf{k}' \right) \\ &=m^2 c^2 + 2 m c \hbar \frac{\omega}{c} - 2 m c \hbar \frac{\omega'}{c}- 2\hbar^2 \left(\frac{\omega}{c} \frac{\omega'}{c}- \mathbf{k} \cdot \mathbf{k}'\right) \\ &=m^2 c^2 + 2 m c \hbar \frac{\omega}{c} - 2 m c \hbar \frac{\omega'}{c}- 2\hbar^2 \frac{\omega}{c} \frac{\omega'}{c} (1 - \cos\theta)\end{aligned}$

Rearranging a bit we have

$\begin{aligned}\omega' \left( m + \frac{\hbar \omega}{c^2} ( 1 - \cos\theta ) \right) = m \omega,\end{aligned} \hspace{\stretch{1}}(2.48)$

$\begin{aligned}\omega' = \frac{\omega}{1 + \frac{\hbar \omega}{m c^2} ( 1 - \cos\theta ) }\end{aligned} \hspace{\stretch{1}}(2.49)$

Pion decay.

The problem above is very much like a midterm problem we had, so there was no justifiable excuse for messing up on it. That midterm problem was to consider the split of a pion at rest into a neutrino (massless) and a muon, and to calculate the energy of the muon. That one also follows the same pattern, a calculation of four momentum conservation, say

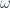$\begin{aligned}(m_\pi c, 0) = \hbar \frac{\omega}{c}(1, \hat{\mathbf{k}}) + ( \mathcal{E}_\mu/c, \mathbf{p}_\mu ).\end{aligned} \hspace{\stretch{1}}(3.50)$

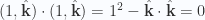Here $\omega$ is the frequency of the massless neutrino. The massless nature is encoded by a four momentum that squares to zero, which follows from $(1, \hat{\mathbf{k}}) \cdot (1, \hat{\mathbf{k}}) = 1^2 - \hat{\mathbf{k}} \cdot \hat{\mathbf{k}} = 0$ .

When I did this problem on the midterm, I perversely put in a scattering angle, instead of recognizing that the particles must scatter at 180 degree directions since spatial momentum components must also be preserved. This and the combination of trying to work in spatial quantities led to a mess and I didn’t get the end result in anything that could be considered tidy.

The simple way to do this is to just rearrange to put the null vector on one side, and then square. This gives us

$\begin{aligned}0 &=\left(\hbar \frac{\omega}{c}(1, \hat{\mathbf{k}}) \right) \cdot\left(\hbar \frac{\omega}{c}(1, \hat{\mathbf{k}}) \right) \\ &=\left( (m_\pi c, 0) - ( \mathcal{E}_\mu/c, \mathbf{p}_\mu ) \right) \cdot \left( (m_\pi c, 0) - ( \mathcal{E}_\mu/c, \mathbf{p}_\mu ) \right) \\ &={m_\pi}^2 c^2 + {m_\nu}^2 c^2 - 2 (m_\pi c, 0) \cdot ( \mathcal{E}_\mu/c, \mathbf{p}_\mu ) \\ &={m_\pi}^2 c^2 + {m_\nu}^2 c^2 - 2 m_\pi \mathcal{E}_\mu\end{aligned}$

A final re-arrangement gives us the muon energy

$\begin{aligned}\mathcal{E}_\mu = \frac{1}{{2}} \frac{ {m_\pi}^2 + {m_\nu}^2 }{m_\pi} c^2\end{aligned} \hspace{\stretch{1}}(3.51)$

Posted in Math and Physics Learning. | Tagged: clifford algebra, cylindrical coordinates, geometric product, Lienard-Wiechert potentials, pauli matrix, PHY450, radiation fields, radioactive decay, relativistic collision | Leave a Comment »

PHY450H1S. Relativistic Electrodynamics Lecture 19 (Taught by Prof. Erich Poppitz). Lienard-Wiechert potentials.

Posted by peeterjoot on April 26, 2011

[Click here for a PDF of this post with nicer formatting (especially if my latex to wordpress script has left FORMULA DOES NOT PARSE errors.)]

Reading.

Covering chapter 8 material from the text [1].

Covering lecture notes pp. 136-146: the Lienard-Wiechert potentials (143-146) [Wednesday, Mar. 9…]

Fields from the Lienard-Wiechert potentials

(We finished off with the scalar and vector potentials in class, but I’ve put those notes with the previous lecture).

To find $\mathbf{E}$ and $\mathbf{B}$ need

$\frac{\partial {t_r}}{\partial {t}}$ , and $\boldsymbol{\nabla} t_r(\mathbf{x}, t)$

where

$\begin{aligned}t - t_r = {\left\lvert{\mathbf{x} - \mathbf{x}_c(t_r) }\right\rvert}\end{aligned} \hspace{\stretch{1}}(2.1)$

implicit definition of $t_r(\mathbf{x}, t)$

In HW5 you’ll show

$\begin{aligned}\frac{\partial {t_r}}{\partial {t}} = \frac{{\left\lvert{\mathbf{x} - \mathbf{x}_c(t_r) }\right\rvert}}{{\left\lvert{\mathbf{x} - \mathbf{x}_c(t_r) }\right\rvert} - \frac{\mathbf{v}_c }{c} \cdot (\mathbf{x} - \mathbf{x}_c(t_r))}\end{aligned} \hspace{\stretch{1}}(2.2)$

$\begin{aligned}\boldsymbol{\nabla} t_r = \frac{1}{{c}} \frac{\mathbf{x} - \mathbf{x}_c(t_r) }{{\left\lvert{\mathbf{x} - \mathbf{x}_c(t_r) }\right\rvert} - \frac{\mathbf{v}_c }{c} \cdot (\mathbf{x} - \mathbf{x}_c(t_r))}\end{aligned} \hspace{\stretch{1}}(2.3)$

and then use this to show that the electric and magnetic fields due to a moving charge are

$\begin{aligned}\mathbf{E}(\mathbf{x}, t) &= \frac{e R}{ (\mathbf{R} \cdot \mathbf{u})^3 } \left( (c^2 - \mathbf{v}_c^2) \mathbf{u} + \mathbf{R} \times (\mathbf{u} \times \mathbf{a}_c) \right) \\ &= \frac{\mathbf{R}}{R} \times \mathbf{E} \\ \mathbf{u} &= c \frac{\mathbf{R}}{R} - \mathbf{v}_c,\end{aligned} \hspace{\stretch{1}}(2.4)$

where everything is evaluated at the retarded time $t_r = t - {\left\lvert{\mathbf{x} - \mathbf{x}_c(t_r)}\right\rvert}/c$ .

This looks quite a bit different than what we find in section 63 (63.8) in the text, but a little bit of expansion shows they are the same.

Check. Particle at rest.

With

$\begin{aligned}\mathbf{x}_c &= \mathbf{x}_0 \\ X_c^k &= (ct, \mathbf{x}_0) \\ {\left\lvert{\mathbf{x} - \mathbf{x}_c(t_r)}\right\rvert} &= c(t - t_r)\end{aligned}$

\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.4\textheight]{particleAtRestTrCalc}
\caption{Retarded time for particle at rest.}

\end{figure}

As illustrated in figure (\ref{fig:particleAtRestTrCalc}) the retarded position is

$\begin{aligned}\mathbf{x}_c(t_r) = \mathbf{x}_0,\end{aligned} \hspace{\stretch{1}}(3.7)$

for

$\begin{aligned}\mathbf{u} = \frac{\mathbf{x} - \mathbf{x}_0}{{\left\lvert{\mathbf{x} - \mathbf{x}_0}\right\rvert}} c,\end{aligned} \hspace{\stretch{1}}(3.8)$

and

$\begin{aligned}\mathbf{E} = e \frac{{ {\left\lvert{\mathbf{x} - \mathbf{x}_0}\right\rvert}} }{ (c {\left\lvert{\mathbf{x} - \mathbf{x}_0}\right\rvert})^3 } c^3 \frac{\mathbf{x} - \mathbf{x}_0}{{{\left\lvert{\mathbf{x} - \mathbf{x}_0}\right\rvert}}},\end{aligned} \hspace{\stretch{1}}(3.9)$

which is Coulomb’s law

$\begin{aligned}\mathbf{E} = e \frac{\mathbf{x} - \mathbf{x}_0}{{\left\lvert{\mathbf{x} - \mathbf{x}_0}\right\rvert}^3}\end{aligned} \hspace{\stretch{1}}(3.10)$

Check. Particle moving with constant velocity.

This was also computed in full in homework 5. The end result was

$\begin{aligned}\mathbf{E} =e \frac{\mathbf{x} - \mathbf{v} t}{{\left\lvert{\mathbf{x} - \mathbf{v} t}\right\rvert}^3}\frac{1 -\boldsymbol{\beta}^2}{ \left(1 - \frac{(\mathbf{x} \times \boldsymbol{\beta})^2}{{\left\lvert{\mathbf{x} - \mathbf{v} t}\right\rvert}^2} \right)^{3/2} }\end{aligned} \hspace{\stretch{1}}(4.11)$

Writing

$\begin{aligned}\frac{\mathbf{x} \times \boldsymbol{\beta}}{{\left\lvert{\mathbf{x} - \mathbf{v} t}\right\rvert}}&=\frac{1}{{c}} \frac{(\mathbf{x} - \mathbf{v} t) \times \mathbf{v}}{{\left\lvert{\mathbf{x} - \mathbf{v} t}\right\rvert}} \\ &=\frac{{\left\lvert{\mathbf{v}}\right\rvert}}{c} \frac{(\mathbf{x} - \mathbf{v} t) \times \mathbf{v}}{{\left\lvert{\mathbf{x} - \mathbf{v} t}\right\rvert} {\left\lvert{\mathbf{v}}\right\rvert}} \end{aligned}$

We can introduce an angular dependence between the charge’s translated position and its velocity

$\begin{aligned}\sin^2 \theta = {\left\lvert{ \frac{\mathbf{v} \times (\mathbf{x} - \mathbf{v} t)}{\Abs{\mathbf{v}} \Abs{\mathbf{x} - \mathbf{v} t}} }\right\rvert}^2,\end{aligned} \hspace{\stretch{1}}(4.12)$

and write the field as

$\begin{aligned}\mathbf{E} =\underbrace{e \frac{\mathbf{x} - \mathbf{v} t}{{\left\lvert{\mathbf{x} - \mathbf{v} t}\right\rvert}^3}}_{{*}}\frac{1 -\boldsymbol{\beta}^2}{ \left(1 - \frac{\mathbf{v}^2}{c^2} \sin^2 \theta \right)^{3/2} }\end{aligned} \hspace{\stretch{1}}(4.13)$

Observe that ${*} = \text{Coulomb's law measured from the instantaneous position of the charge}$ .

The electric field $\mathbf{E}$ has a time dependence, strongest when perpendicular to the instantaneous position when $\theta = \pi/2$ , since the denominator is smallest ( $\mathbf{E}$ largest) when $\mathbf{v}/c$ is not small. This is strongly $\theta$ dependent.

Compare

$\begin{aligned}\frac{{\left\lvert{\mathbf{E}(\theta = \pi/2)}\right\rvert} - {\left\lvert{\mathbf{E}(\theta = \pi/2 + \Delta \theta)}\right\rvert} }{{\left\lvert{\mathbf{E}(\theta = \pi/2)}\right\rvert}}&\approx\frac{\frac{1}{{(1 - \mathbf{v}^2/c^2)^{3/2}}} - \frac{1}{{(1 - \mathbf{v}^2/c^2(1 - (\Delta \theta)^2))^{3/2}}}}{\frac{1}{{(1 - \mathbf{v}^2/c^2)^{3/2}}}} \\ &=1 - \left(\frac{1 - \mathbf{v}^2/c^2}{1 - \mathbf{v}^2/c^2 + \mathbf{v}^2/c^2(\Delta \theta)^2}\right)^{3/2} \\ &=1 - \left(\frac{1}{1 + \mathbf{v}^2/c^2 \frac{(\Delta \theta)^2}{1 - \mathbf{v}^2/c^2}}\right)^{3/2} \\ \end{aligned}$

Here we used

$\begin{aligned}\sin(\theta + \pi/2) = \frac{e^{i (\theta + \pi/2)} - e^{-i(\theta + \pi/2)}}{2i} = \cos\theta \end{aligned} \hspace{\stretch{1}}(4.14)$

and

$\begin{aligned}\cos^2 \Delta \theta \approx \left( 1 - \frac{(\Delta \theta)^2}{2} \right)^2 \approx 1 - (\Delta \theta)^2\end{aligned} \hspace{\stretch{1}}(4.15)$

FIXME: he writes:

$\begin{aligned}\Delta \theta \le \sqrt{1 - \frac{\mathbf{v}^2}{c^2}}\end{aligned} \hspace{\stretch{1}}(4.16)$

I don’t see where that comes from.

FIXME: PICTURE: Various $\mathbf{E}$ ‘s up, and $\mathbf{v}$ perpendicular to that, strongest when charge is moving fast.

Back to extracting physics from the Lienard-Wiechert field equations

Imagine that we have a localized particle motion with

$\begin{aligned}{\left\lvert{\mathbf{x}_c(t_r)}\right\rvert} < l\end{aligned} \hspace{\stretch{1}}(5.17)$

The velocity vector

$\begin{aligned}\mathbf{u} = c \frac{\mathbf{x} - \mathbf{x}_c(t_r)}{{\left\lvert{\mathbf{x} - \mathbf{x}_c}\right\rvert}}\end{aligned} \hspace{\stretch{1}}(5.18)$

doesn’t grow as distance from the source, so from 2.4, we have for ${\left\lvert{\mathbf{x}}\right\rvert} \gg l$

$\begin{aligned}\mathbf{B}, \mathbf{E} \sim \frac{1}{{{\left\lvert{\mathbf{x}}\right\rvert}^2}}(\cdots) + \frac{1}{\mathbf{x}}(\text{acceleration term})\end{aligned} \hspace{\stretch{1}}(5.19)$

The acceleration term will dominate at large distances from the source. Our Poynting magnitude is

$\begin{aligned}{\left\lvert{\mathbf{S}}\right\rvert} \sim {\left\lvert{\mathbf{E} \times \mathbf{B}}\right\rvert} \sim \frac{1}{{\mathbf{x}^2}} (\text{acceleration})^2.\end{aligned} \hspace{\stretch{1}}(5.20)$

We can ask about

$\begin{aligned}\oint d^2 \boldsymbol{\sigma} \cdot \mathbf{S} \sim R^2 \frac{1}{{R^2}} (\text{acceleration})^2 \sim (\text{acceleration})^2 \end{aligned} \hspace{\stretch{1}}(5.21)$

In the limit, for the radiation of EM waves

$\begin{aligned}\lim_{R\rightarrow \infty} \oint d^2 \boldsymbol{\sigma} \cdot \mathbf{S} \ne 0\end{aligned} \hspace{\stretch{1}}(5.22)$

The energy flux through a sphere of radius $R$ is called the radiated power.

References

[1] L.D. Landau and E.M. Lifshitz. The classical theory of fields. Butterworth-Heinemann, 1980.

Posted in Math and Physics Learning. | Tagged: Lienard-Wiechert fields, Lienard-Wiechert potentials, PHY450, radiated power | Leave a Comment »

Collection of PHY450HS1 (relativistic electrodynamics) class notes and worked problems.

Posted by peeterjoot on April 11, 2011

Before the midterm I’d posted a collection of my class notes as of that point in time.

That collection is now updated and except for Lecture 19 on the Lienard-Wiechard potentials and the last lecture on third order radiation effects, now covers most of what our Professor covered in class. This includes all of the following individual bits (in reverse chronological order)

April 10, 2011 Three dimensional divergence theorem with generally parametrized volume element.

April 5, 2011 PHY450H1S. Relativistic Electrodynamics Lecture 26 (Taught by Prof. Erich Poppitz). Radiation reaction force for a dipole system.

Mar 31, 2011 PHY450H1S. Relativistic Electrodynamics Lecture 25 (Taught by Prof. Erich Poppitz). Second order interaction, the Darwin Lagrangian.

Mar 30, 2011 PHY450H1S. Relativistic Electrodynamics Tutorial 9 (TA: Simon Freedman). Some worked problems. EM reflection. Stress energy tensor for simple configurations.

Mar 30, 2011 PHY450H1S. Relativistic Electrodynamics Lecture 24 (Taught by Prof. Erich Poppitz). Non-relativistic electrostatic Lagrangian.

Mar 29, 2011 PHY450H1S. Relativistic Electrodynamics Lecture 23 (Taught by Prof. Erich Poppitz). Energy Momentum Tensor.

Mar 25, 2011 Problem Set 6.

Mar 23, 2011 PHY450H1S. Relativistic Electrodynamics Tutorial 8 (TA: Simon Freedman). EM fields from magnetic dipole current.

Mar 23, 2011 Energy Momentum Tensor.

Mar 22, 2011 PHY450H1S. Relativistic Electrodynamics Lecture 21 (Taught by Prof. Erich Poppitz). More on EM fields due to dipole radiation.

Mar 15, 2011 PHY450H1S. Relativistic Electrodynamics Lecture 20 (Taught by Prof. Erich Poppitz). Potentials at a distance from a localized current distribution. EM fields due to dipole radiation.

Mar 14, 2011 Problem Set 5.

Mar 10, 2011 PHY450H1S. Relativistic Electrodynamics Tutorial 5 (TA: Simon Freedman). Angular momentum of EM fields

Mar 9, 2011 PHY450H1S. Relativistic Electrodynamics Lecture 18 (Taught by Prof. Erich Poppitz). Green’s function solution to Maxwell’s equation.

Mar 8, 2011 PHY450H1S. Relativistic Electrodynamics Lecture 17 (Taught by Prof. Erich Poppitz). Energy and momentum density. Starting a Green’s function solution to Maxwell’s equation.

Mar 3, 2011 PHY450H1S. Relativistic Electrodynamics Tutorial 4 (TA: Simon Freedman). Waveguides: confined EM waves.

Mar 3, 2011 PHY450H1S Problem Set 4.

Mar 2, 2011 PHY450H1S. Relativistic Electrodynamics Lecture 16 (Taught by Prof. Erich Poppitz). Monochromatic EM fields. Poynting vector and energy density conservation.

Mar 1, 2011 PHY450H1S. Relativistic Electrodynamics Lecture 15 (Taught by Prof. Erich Poppitz). Fourier solution of Maxwell’s vacuum wave equation in the Coulomb gauge.

Feb 16, 2011 PHY450H1S. Relativistic Electrodynamics Lecture 14 (Taught by Simon Freedman). Wave equation in Coulomb and Lorentz gauges.

Feb 15, 2011 PHY450H1S. Relativistic Electrodynamics Lecture 13 (Taught by Prof. Erich Poppitz). Variational principle for the field.

Feb 15, 2011 PHY450H1S Problem Set 3.

Feb 10, 2011 PHY450H1S. Relativistic Electrodynamics Lecture 12 (Taught by Prof. Erich Poppitz). Action for the field.

Feb 9, 2011 PHY450H1S. Relativistic Electrodynamics Lecture 11 (Taught by Prof. Erich Poppitz). Unpacking Lorentz force equation. Lorentz transformations of the strength tensor, Lorentz field invariants, Bianchi identity, and first half of Maxwell’s.

Feb 8, 2011 PHY450H1S. Relativistic Electrodynamics Lecture 10 (Taught by Prof. Erich Poppitz). Lorentz force equation energy term, and four vector formulation of the Lorentz force equation.

Feb 6, 2011 Energy term of the Lorentz force equation.

Feb 3, 2011 PHY450H1S. Relativistic Electrodynamics Tutorial 3 (TA: Simon Freedman). Relativistic motion in constant uniform electric or magnetic fields.

Feb 1, 2011 PHY450H1S Problem Set 2.

Feb 1, 2011 PHY450H1S. Relativistic Electrodynamics Lecture 9 (Taught by Prof. Erich Poppitz). Dynamics in a vector field.

Feb 1, 2011 PHY450H1S. Relativistic Electrodynamics Lecture 8 (Taught by Prof. Erich Poppitz). Relativistic dynamics.

Jan 27, 2011 PHY450H1S. Relativistic Electrodynamics Tutorial 2 (TA: Simon Freedman). Two worked problems.

Jan 26, 2011 PHY450H1S. Relativistic Electrodynamics Lecture 7 (Taught by Prof. Erich Poppitz). Action and relativistic dynamics.

Jan 25, 2011 PHY450H1S. Relativistic Electrodynamics Lecture 6 (Taught by Prof. Erich Poppitz). Four vectors and tensors.

Jan 22, 2011 PHY450H1S Problem Set 1.

Jan 20, 2011 Four vectors and a worked problem on energy flux density.

Jan 18, 2011 Proper time, length contraction, time dialation, causality.

Jan 18, 2011 Spacetime geometry, Lorentz transformations, Minkowski diagrams.

Jan 14, 2011 Some tensor and geometric algebra comparisons in a spacetime context.

Jan 14, 2011 Lorentz transformation of an antisymmetric tensor.

Jan 13, 2011 Spacetime, events, worldlines, spacetime intervals, and invariance.

Jan 12, 2011 Spacetime, events, worldlines, proper time, invariance.

Jan 11, 2011 Speed of light and simultaneity.

Posted in Math and Physics Learning. | Tagged: PHY450 | Leave a Comment »

PHY450H1S. Relativistic Electrodynamics Lecture 26 (Taught by Prof. Erich Poppitz). Radiation reaction force for a dipole system.

Posted by peeterjoot on April 11, 2011

[Click here for a PDF of this post with nicer formatting (especially if my latex to wordpress script has left FORMULA DOES NOT PARSE errors.)]

Reading.

Covering chapter 8 section 65 material from the text [1].

Covering pp. 181-195: (182-189) [Tuesday, Mar. 29]; the EM potentials to order $(v/c)^2$ (190-193); the “Darwin Lagrangian. and Hamiltonian for a system of nonrelativistic charged particles to order $(v/c)^2$ and its many uses in physics (194-195) [Wednesday, Mar. 30]

Next week (last topic): attempt to go to the next order $(v/c)^3$ – radiation damping, the limitations of classical electrodynamics, and the relevant time/length/energy scales.

Recap.

A system of N charged particles $m_a, q_a ; a \in [1, N]$ closed system and nonrelativistic, $v_a/c \ll 1$ . In this case we can incorporate EM effects in a Largrangian ONLY involving particles (EM field not a dynamical DOF). In general case, this works to $O((v/c)^2)$ , because at $O((v/c))$ system radiation effects occur.

In a specific case, when

$\begin{aligned}\frac{m_1}{q_1} = \frac{m_2}{q_2} = \frac{m_3}{q_3} = \cdots\end{aligned} \hspace{\stretch{1}}(2.1)$

we can do that (meaning use a Lagrangian with particles only) to $O((v/c)^4)$ because of specific symmetries in such a system.

The Lagrangian for our particle after the gauge transformation is

$\begin{aligned}\mathcal{L}_a = \frac{1}{{2}} m_a \mathbf{v}_a^2 + \frac{m_a}{8} \frac{\mathbf{v}_a^4}{c^2} -\sum_{b \ne a} \frac{q_a q_b}{{\left\lvert{\mathbf{x}_a(t) - \mathbf{x}_b(t)}\right\rvert}}+\sum_b q_a q_b \frac{\mathbf{v}_a \cdot \mathbf{v}_b + (\mathbf{n} \cdot \mathbf{v}_a) (\mathbf{n} \cdot \mathbf{v}_b)}{2 c^2 {\left\lvert{\mathbf{x} - \mathbf{x}_b}\right\rvert} }.\end{aligned} \hspace{\stretch{1}}(2.2)$

Next time we’ll probably get to the Lagrangian for the entire system. It was hinted that this is called the Darwin Lagrangian (after Charles Darwin’s grandson).

We find for whole system

$\begin{aligned}\mathcal{L} = \sum_a \mathcal{L}_a + \frac{1}{{2}} \sum_a \mathcal{L}_a (interaction)\end{aligned} \hspace{\stretch{1}}(2.3)$

$\begin{aligned}\mathcal{L} = \frac{1}{{2}} \sum_a m_a \mathbf{v}_a^2 + \sum_a \frac{m_a}{8} \frac{\mathbf{v}_a^4}{c^2} -\sum_{ a < b} \frac{q_a q_b}{{\left\lvert{\mathbf{x}_a(t) - \mathbf{x}_b(t)}\right\rvert}}+\sum_b q_a q_b \frac{\mathbf{v}_a \cdot \mathbf{v}_b + (\mathbf{n} \cdot \mathbf{v}_a) (\mathbf{n} \cdot \mathbf{v}_b)}{2 c^2 {\left\lvert{\mathbf{x} - \mathbf{x}_b}\right\rvert} }.\end{aligned} \hspace{\stretch{1}}(2.4)$

This is the Darwin Lagrangian (also Charles). The Darwin Hamiltonian is then

$\begin{aligned}H = \sum_a \frac{p_a}{2 m_a} \mathbf{v}_a^2 + \sum_a \frac{p_a^4}{8 m_a^3 c^2} +\sum_{ a < b} \frac{q_a q_b}{{\left\lvert{\mathbf{x}_a(t) - \mathbf{x}_b(t)}\right\rvert}}- \sum_{ a < b } \frac{q_a q_b}{ 2 c^2 m_a m_b } \frac{\mathbf{p}_a \cdot \mathbf{p}_b + (\mathbf{n}_{a b} \cdot \mathbf{p}_a) (\mathbf{n}_{ a b } \cdot \mathbf{p}_b)}{{\left\lvert{\mathbf{x} - \mathbf{x}_b}\right\rvert} }.\end{aligned} \hspace{\stretch{1}}(2.5)$

Incorporating radiation effects as a friction term.

To $O((v/c)^3)$ obvious problem due to radiation (system not closed). We’ll incorporate radiation via a function term in the EOM

Again consider the dipole system

$\begin{aligned}m \dot{d}{z} &= -k z \\ \omega^2 &= \frac{k}{m}\end{aligned} \hspace{\stretch{1}}(3.6)$

$\begin{aligned}m \dot{d}{z} = -\omega^2 m z\end{aligned} \hspace{\stretch{1}}(3.8)$

gives

$\begin{aligned}\frac{d{{}}}{dt}\left( \frac{m}{2} \dot{z}^2 + \frac{ m \omega^2 }{2} z^2 \right) = 0 \end{aligned} \hspace{\stretch{1}}(3.9)$

(because there’s no radiation).

The energy radiated per unit time averaged per period is

$\begin{aligned}P = \frac{ 2 e^2 }{ 3 c^3} \left\langle{{ \dot{d}{z}^2 }}\right\rangle\end{aligned} \hspace{\stretch{1}}(3.10)$

We’ll modify the EOM

$\begin{aligned}m \dot{d}{z} = -\omega^2 m z + f_{\text{radiation}}\end{aligned} \hspace{\stretch{1}}(3.11)$

Employing an integration factor $\dot{z}$ we have

$\begin{aligned}m \dot{d}{z} \dot{z} = -\omega^2 m z \dot{z} + f_{\text{radiation}} \dot{z}\end{aligned} \hspace{\stretch{1}}(3.12)$

$\begin{aligned}\frac{d{{}}}{dt} \left( m \dot{z}^2 + \omega^2 m z^2 \right) = f_{\text{radiation}} \dot{z}\end{aligned} \hspace{\stretch{1}}(3.13)$

Observe that the last expression, force times velocity, has the form of power

$\begin{aligned}m \frac{d^2 z}{dt^2} \frac{dz}{dt} = \frac{d{{}}}{dt} \left( \frac{m}{2} \left( \frac{dz}{dt} \right)^2 \right)\end{aligned} \hspace{\stretch{1}}(3.14)$

So we can make an identification with the time rate of energy lost by the system due to radiation

$\begin{aligned}\frac{d{{}}}{dt} \left( m \dot{z}^2 + \omega^2 m z^2 \right) \equiv \frac{d{{\mathcal{E}}}}{dt}.\end{aligned} \hspace{\stretch{1}}(3.15)$

Average over period both sides

$\begin{aligned}\left\langle{{ \frac{d{{\mathcal{E}}}}{dt} }}\right\rangle = \left\langle{{ f_{\text{radiation}} \dot{z} }}\right\rangle=- \frac{2 e^2 }{3 c^3} \left\langle{{\dot{d}{z}^2}}\right\rangle\end{aligned} \hspace{\stretch{1}}(3.16)$

We demand this last equality, by requiring the energy change rate to equal that of the dipole power (but negative since it is a loss) that we previously calculated.

Claim:

$\begin{aligned}f_{\text{radiation}} = \frac{2 e^2 }{3 c^3} \dddot{z}\end{aligned} \hspace{\stretch{1}}(3.17)$

Proof:

We need to show

$\begin{aligned}\left\langle{{ f_{\text{radiation}} }}\right\rangle= - \frac{2 e^2 }{3 c^3} \left\langle{{\dot{d}{z}^2}}\right\rangle\end{aligned} \hspace{\stretch{1}}(3.18)$

We have

$\begin{aligned}\frac{2 e^2}{3 c^3} \left\langle{{ \dddot{z} \dot{z} }}\right\rangle &= \frac{2 e^2}{3 c^3} \frac{1}{{T}} \int_0^T dt \dddot{z} \dot{z} \\ &= \frac{2 e^2}{3 c^3} \frac{1}{{T}} \int_0^T dt {\frac{d{{}}}{dt} (\dot{d}{z} \dot{z}) }-\frac{2 e^2}{3 c^3} \frac{1}{{T}} \int_0^T dt (\dot{d}{z})^2\end{aligned}$

We first used $(\dot{d}{z} \dot{z})' = \dddot{z} \dot{z} + (\dot{d}{z})^2$ . The first integral above is zero since the derivative of $\dot{d}{z} \dot{z} = (-\omega^2 z_0 \sin\omega t)(\omega z_0 \cos\omega t) = -\omega^3 z_0^2 \sin(2 \omega t)/2$ is also periodic, and vanishes when integrated over the interval.

$\begin{aligned}\frac{2 e^2}{3 c^3} \left\langle{{ \dddot{z} \dot{z} }}\right\rangle =-\frac{2 e^2}{3 c^3} \left\langle{{ (\dot{d}{z})^2 }}\right\rangle\end{aligned} \hspace{\stretch{1}}(3.19)$

We can therefore write

$\begin{aligned}m \dot{d}{z} = -m \omega^2 z + \frac{2 e^2}{3 c^3} \dddot{z}\end{aligned} \hspace{\stretch{1}}(3.20)$

Our “frictional” correction is the radiation reaction force proportional to the third derivative of the position.

Rearranging slightly, this is

$\begin{aligned}\dot{d}{z} = - \omega^2 z + \frac{2}{3 c} \left( \frac{e^2}{m c^2} \right) \dddot{z} = - \omega^2 z + \frac{2}{3 c} \frac{r_e}{c} \dddot{z},\end{aligned} \hspace{\stretch{1}}(3.21)$

where $r_e \sim 10^{-13} \text{cm}$ is the “classical radius” of the electron. In our frictional term we have $r_e/c$ , the time for light to cross the classical radius of the electron.

There are lots of problems with this. One of the easiest is with $\omega = 0$ . Then we have

$\begin{aligned}\dot{d}{z} = \frac{2}{3} \frac{r_e}{c} \dddot{z}\end{aligned} \hspace{\stretch{1}}(3.22)$

with solution

$\begin{aligned}z \sim e^{\alpha t},\end{aligned} \hspace{\stretch{1}}(3.23)$

where

$\begin{aligned}\alpha \sim \frac{c}{r_e} \sim \frac{1}{{\tau_e}}.\end{aligned} \hspace{\stretch{1}}(3.24)$

This is a self accelerating system! Note that we can also get into this trouble with $\omega \ne 0$ , but those examples are harder to find (see: [2]).

FIXME: borrow this text again to give that section a read.

The sensible point of view is that this third term ( $f_{\text{rad}}$ ) should be taken seriously only if it is small compared to the first two terms.

References

[1] L.D. Landau and E.M. Lifshitz. The classical theory of fields. Butterworth-Heinemann, 1980.

[2] D.J. Griffith. Introduction to Electrodynamics. Prentice-Hall, 1981.

Posted in Math and Physics Learning. | Tagged: dipole radiation, PHY450, radiation reaction force | Leave a Comment »

PHY450H1S. Relativistic Electrodynamics Tutorial 9 (TA: Simon Freedman). Some worked problems. EM reflection. Stress energy tensor for simple configurations.

Posted by peeterjoot on April 11, 2011

[Click here for a PDF of this post with nicer formatting (especially if my latex to wordpress script has left FORMULA DOES NOT PARSE errors.)]

HW6. Question 3. (Non subtle hints about how important this is (i.e. for the exam)

Motivation.

This is problem 1 from section 47 of the text [1].

Determine the force exerted on a wall from which an incident plane EM wave is reflected (w/ reflection coefficient $R$ ) and incident angle $\theta$ .

Solution from the book

$\begin{aligned}f_\alpha = - \sigma_{\alpha \beta} n_\beta - {\sigma'}_{\alpha \beta} n_\beta\end{aligned} \hspace{\stretch{1}}(1.1)$

Here $\sigma_{\alpha \beta}$ is the Maxwell stress tensor for the incident wave, and ${\sigma'}_{\alpha \beta}$ is the Maxwell stress tensor for the reflected wave, and $n_\beta$ is normal to the wall.

On the signs of the force per unit area

The signs in 1.1 require a bit of thought. We have for the rate of change of the $\alpha$ component of the field momentum

$\begin{aligned}\frac{d{{}}}{dt} \int d^3 \mathbf{x} \left( \frac{S^\alpha}{c^2} \right) = - \int d^2 \sigma^\beta T^{\beta \alpha}\end{aligned} \hspace{\stretch{1}}(1.2)$

where $d^2 \sigma^\beta = d^2 \sigma \mathbf{n} \cdot \mathbf{e}_\beta$ , and $\mathbf{n}$ is the outwards unit normal to the surface. This is the rate of change of momentum for the field, the force on the field. For the force on the wall per unit area, we wish to invert this, giving

$\begin{aligned}df^\alpha_{\text{on the wall, per unit area}}= (\mathbf{n} \cdot \mathbf{e}_\beta) T^{\beta \alpha}= -(\mathbf{n} \cdot \mathbf{e}_\beta) \sigma_{\beta \alpha}\end{aligned} \hspace{\stretch{1}}(1.3)$

Returning to the tutorial notes

Simon writes

$\begin{aligned}f_\perp &= - \sigma_{\perp \perp} - {\sigma'}_{\perp \perp} \\ f_\parallel &= - \sigma_{\parallel \perp} - {\sigma'}_{\parallel \perp} \end{aligned} \hspace{\stretch{1}}(1.4)$

and then says stating this solution is very non-trivial, because $\sigma_{\alpha \beta}$ is non-linear in $\mathbf{E}$ and $\mathbf{B}$ . This non-triviality is a good point. Without calculating it, I find the results above to be pulled out of a magic hat. The point of the tutorial discussion was to work through this in detail.

Working out the tensor.

FIXME: PICTURE:

The Reflection coefficient can be defined in this case as

$\begin{aligned}R = \frac{ {\left\lvert{\mathbf{E}'}\right\rvert}^2 }{ {\left\lvert{\mathbf{E}}\right\rvert}^2 },\end{aligned} \hspace{\stretch{1}}(2.6)$

a ratio of the powers of the reflected wave power to the incident wave power (which are proportional to ${\mathbf{E}'}^2$ and ${\mathbf{E}}^2$ respectively.

Suppose we pick the following orientation for the incident fields

$\begin{aligned}E_x &= E \sin\theta \\ E_y &= -E \cos\theta \\ B_z &= E ,\end{aligned} \hspace{\stretch{1}}(2.7)$

With the reflected assumed to be in some still perpendicular orientation (with this orientation picked for convienence)

$\begin{aligned}E_x' &= E' \sin\theta \\ E_y' &= E' \cos\theta \\ B_z' &= E'.\end{aligned} \hspace{\stretch{1}}(2.10)$

Here

$\begin{aligned}E &= E_0 \cos(\mathbf{p} \cdot \mathbf{x} - \omega t) \\ E' &= \sqrt{R} E_0 \cos(\mathbf{p}' \cdot \mathbf{x} - \omega t)\end{aligned} \hspace{\stretch{1}}(2.13)$

FIXME: there are assumptions below that $\mathbf{p}' \cdot \mathbf{x} = \mathbf{p} \cdot \mathbf{x}$ . I don’t see where that comes from, since the propagation directions are difference for the incident and the reflected waves.

$\begin{aligned}\sigma_{\alpha\beta} = -T^{\alpha\beta} = \frac{1}{{4\pi}} \left(\mathcal{E}^\alpha\mathcal{E}^\beta+\mathcal{B}^\alpha\mathcal{B}^\beta- \frac{1}{{2}} \delta^{\alpha\beta} ( \vec{\mathcal{E}}^2 + \vec{\mathcal{B}}^2 )\right)\end{aligned} \hspace{\stretch{1}}(2.15)$

Aside: On the geometry, and the angle of incidence.

According to wikipedia [2] the angle of incidence is measured from the normal.

Let’s use complex numbers to get the orientation of the electric and propagation direction fields right. We have for the incident propagation direction

$\begin{aligned}-\hat{\mathbf{p}} \sim e^{i (\pi + \theta) }\end{aligned} \hspace{\stretch{1}}(2.16)$

$\begin{aligned}\hat{\mathbf{p}} \sim e^{i\theta}\end{aligned} \hspace{\stretch{1}}(2.17)$

If we pick the electric field rotated negatively from that direction, we have

$\begin{aligned}\hat{\mathbf{E}} &\sim -i e^{i \theta} \\ &= -i (\cos\theta + i \sin\theta) \\ &= -i \cos\theta + \sin\theta\end{aligned}$

$\begin{aligned}E_x &\sim \sin\theta \\ E_y &\sim -\cos\theta\end{aligned} \hspace{\stretch{1}}(2.18)$

For the reflected direction we have

$\begin{aligned}\hat{\mathbf{p}}' \sim e^{i (\pi - \theta)} = - e^{-i \theta}\end{aligned} \hspace{\stretch{1}}(2.20)$

rotating negatively for the electric field direction, we have

$\begin{aligned}\hat{\mathbf{E}'} &\sim -i (- e^{-i\theta} ) \\ &= i(cos\theta - i\sin\theta) \\ &= i cos\theta + \sin\theta\end{aligned}$

$\begin{aligned}E_x' &\sim \sin\theta \\ E_y' &\sim \cos\theta \end{aligned} \hspace{\stretch{1}}(2.21)$

Back to the problem (again).

Where $\vec{\mathcal{E}}$ and $\vec{\mathcal{B}}$ are the total EM fields.

\paragraph{Aside:} Why the fields are added in this fashion wasn’t clear to me, but I guess this makes sense. Even if the propagation directions differ, the total field at any point is still just a superposition.

$\begin{aligned}\vec{\mathcal{E}} &= \mathbf{E} + \mathbf{E}' \\ \vec{\mathcal{B}} &= \mathbf{B} + \mathbf{B}'\end{aligned} \hspace{\stretch{1}}(2.23)$

Get

$\begin{aligned}\sigma_{3 3} &= \frac{1}{{4 \pi}} \left( \underbrace{B_z B_z}_{=\vec{\mathcal{B}}^2} - \frac{1}{{2}} (\vec{\mathcal{E}}^2 + \vec{\mathcal{B}}^2) \right) = 0 \\ \sigma_{3 1} &= 0 = \sigma_{3 2} \\ \sigma_{1 1} &= \frac{1}{{4 \pi}} \left( (\mathcal{E}^1)^2 - \frac{1}{{2}} (\vec{\mathcal{E}}^2 + \vec{\mathcal{B}}^2) \right) \end{aligned} \hspace{\stretch{1}}(2.25)$

$\begin{aligned}\vec{\mathcal{B}}^2 &= (B_z + B_z')^2 = (E + E')^2 \\ \vec{\mathcal{E}}^2 &= (\mathbf{E} + \mathbf{E}')^2\end{aligned} \hspace{\stretch{1}}(2.28)$

$\begin{aligned}\sigma_{1 1} &= \frac{1}{{4 \pi}} \left( (\mathcal{E}^1)^2 - \frac{1}{{2}} ((\mathcal{E}^1)^2 + (\mathcal{E}^2)^2 + (E + E')^2 \right) \\ &= \frac{1}{{8 \pi}} \left( (\mathcal{E}^1)^2 - (\mathcal{E}^2)^2 - (E + E')^2 \right) \\ &= \frac{1}{{8 \pi}} \left( (E + E')^2 \sin^2\theta -(E' - E)^2 \cos^2\theta -(E + E')^2\right) \\ &= \frac{1}{{8 \pi}} \left( E^2( \sin^2\theta - \cos^2\theta - 1)+(E')^2( \sin^2\theta - \cos^2\theta - 1)+ 2 E E' (\sin^2\theta + \cos^2\theta -1 )\right) \\ &= \frac{1}{{8 \pi}} \left( - 2 E^2 \cos^2\theta - 2 (E')^2 \cos^2\theta \right) \\ &= -\frac{1}{{4 \pi}} (E^2 + (E')^2) \cos^2\theta \\ &= \sigma_\parallel + {\sigma'}_\parallel\end{aligned}$

This last bit I didn’t get. What is $\sigma_\parallel$ and ${\sigma'}_\parallel$ . Are these parallel to the wall or parallel to the normal to the wall. It turns out that this appears to mean parallel to the normal. We can see this by direct calculation

$\begin{aligned}\sigma_{x x}^{\text{incident}} &= \frac{1}{{4 \pi}} \left( E_x^2 - \frac{1}{{2}} (\mathbf{E}^2 + \mathbf{B}^2)\right) \\ &= \frac{1}{{4 \pi}} \left( E^2 \sin^2 \theta - \frac{1}{{2}} 2 E^2 \right) \\ &= -\frac{1}{{4 \pi}} E^2 \cos^2\theta\end{aligned}$

$\begin{aligned}{\sigma}_{x x}^{\text{reflected}} &= \frac{1}{{4 \pi}} \left( {E_x'}^2 - \frac{1}{{2}} ({\mathbf{E}'}^2 + {\mathbf{B}'}^2)\right) \\ &= \frac{1}{{4 \pi}} \left( {E'}^2 \sin^2 \theta - \frac{1}{{2}} 2 {E'}^2 \right) \\ &= -\frac{1}{{4 \pi}} {E'}^2 \cos^2\theta\end{aligned}$

So by comparison we see that we have

$\begin{aligned}\sigma_{1 1} = {\sigma}_{x x}^{\text{incident}} +{\sigma}_{x x}^{\text{reflected}} \end{aligned} \hspace{\stretch{1}}(2.30)$

Moving on, for our other component on the $x,y$ place $\sigma_{12}$ we have

$\begin{aligned}\sigma_{12} &= \frac{1}{{4 \pi}} \mathcal{E}^1 \mathcal{E}^2 \\ &= \frac{1}{{4 \pi}} (E + E') \sin\theta (-E + E') \cos\theta \\ &= \frac{1}{{4 \pi}} ((E')^2 - E^2) \sin\theta \cos\theta \end{aligned}$

Again we can compare to the sums of the reflected and incident tensors for this $x,y$ component. Those are

$\begin{aligned}\sigma_{12}^{\text{incident}} &= \frac{1}{{4 \pi}} ( E^1 E^2 ) \\ &= -\frac{1}{{4 \pi}} E^2 \sin\theta \cos\theta,\end{aligned}$

and

$\begin{aligned}\sigma_{12}^{\text{reflected}} &= \frac{1}{{4 \pi}} ( {E'}^1 {E'}^2 ) \\ &= \frac{1}{{4 \pi}} {E'}^2 \sin\theta \cos\theta\end{aligned}$

Which demonstrates that we have

$\begin{aligned}\sigma_{12} = \sigma_{12}^{\text{incident}} + \sigma_{12}^{\text{reflected}} \end{aligned} \hspace{\stretch{1}}(2.31)$

Summarizing, for the components in the $x,y$ plane we have found that we have

$\begin{aligned}\sigma_{\alpha\beta}^{\text{total}} n_\beta = \sigma_{\alpha 1 }^{\text{total}} = \sigma_{\alpha 1} + {\sigma'}_{\alpha 1}\end{aligned} \hspace{\stretch{1}}(2.32)$

(where $n_\beta = \delta^{\beta 1}$ )

This result, assumed in the text, was non-trivial to derive. It is also not generally true. We have

$\begin{aligned}\sigma_{2 2} &= \frac{1}{{4 \pi}} \left( (\mathcal{E}^y)^2 - \frac{1}{{2}} ( \vec{\mathcal{E}}^2 + \vec{\mathcal{B}}^2 ) \right) \\ &= \frac{1}{{8 \pi}} \left( (\mathcal{E}^y)^2 - (\mathcal{E}^x)^2 - \vec{\mathcal{B}}^2 ) \right) \\ &= \frac{1}{{8 \pi}} \left( (E' - E)^2 \cos^2\theta - (E + E')^2 \sin^2\theta - (E + E')^2\right) \\ &= \frac{1}{{8 \pi}} \left( E^2 ( -1 + \cos^2 \theta - \sin^2\theta )+{E'}^2 ( -1 + \cos^2 \theta - \sin^2\theta )+ 2 E E' ( -\cos^2\theta - \sin^2\theta -1 ) \right) \\ &= -\frac{1}{{4 \pi}} \left( E^2 \sin^2 \theta + (E')^2 \sin^2 \theta + 2 E E' \right)\end{aligned}$

If we compare to the incident and reflected tensors we have

$\begin{aligned}\sigma_{y y}^{\text{incident}} &= \frac{1}{{4 \pi}} \left( (E^y)^2 -\frac{1}{{2}} E^2 \right) \\ &= \frac{1}{{4 \pi}} E^2 ( \cos^2\theta - 1 ) \\ &= -\frac{1}{{4 \pi}} E^2 \sin^2\theta \end{aligned}$

and

$\begin{aligned}\sigma_{y y}^{\text{reflected}} &= \frac{1}{{4 \pi}} \left( ({E'}^y)^2 -\frac{1}{{2}} {E'}^2 \right) \\ &= \frac{1}{{4 \pi}} {E'}^2 ( \cos^2\theta - 1 ) \\ &= -\frac{1}{{4 \pi}} {E'}^2 \sin^2\theta \end{aligned}$

There’s a cross term that we can’t have summing the two, so we have, in general

$\begin{aligned}\sigma_{2 2}^{\text{total}} \ne \sigma_{y y}^{\text{incident}} +\sigma_{y y}^{\text{reflected}} \end{aligned} \hspace{\stretch{1}}(2.33)$

Force per unit area?

$\begin{aligned}f_\alpha = n^x \sigma_{x \alpha} \end{aligned} \hspace{\stretch{1}}(2.34)$

Averaged

$\begin{aligned}\left\langle{{\sigma_{xx}}}\right\rangle &= -\frac{1}{{8 \pi}} E_0^2 ( 1 + R) \cos^2\theta \\ \left\langle{{\sigma_{xy}}}\right\rangle &= -\frac{1}{{8 \pi}} E_0^2 ( 1 - R) \sin\theta \cos\theta\end{aligned} \hspace{\stretch{1}}(2.35)$

$\begin{aligned}\left\langle{\mathbf{S}}\right\rangle &= -\frac{c}{8 \pi} E_0^2 \hat{\mathbf{n}} \\ \left\langle{{\mathbf{S}'}}\right\rangle &= -\frac{c}{8 \pi} E_0^2 \hat{\mathbf{n}}'\end{aligned} \hspace{\stretch{1}}(2.37)$

$\begin{aligned}\left\langle{{{\left\lvert{\mathbf{S}}\right\rvert}}}\right\rangle = \text{Work} = W\end{aligned} \hspace{\stretch{1}}(2.39)$

$\begin{aligned}f_x &= n^x \sigma_{x x} = W (1 + R) \cos^2\theta \\ f_y &= n^y \sigma_{x y} = W (1 - R) \sin\theta \cos\theta \\ f_z &= 0\end{aligned} \hspace{\stretch{1}}(2.40)$

A problem from Griffiths.

FIXME: try this.

Two charges $q+$ , $q-$ reflected in a plane, separated by distance $a$ . Work out the stress energy tensor from the Coulomb fields of the charges on the plane.

Will get the Coulomb force:

$\begin{aligned}\mathbf{F} = k \frac{q^2}{2 a^2}.\end{aligned} \hspace{\stretch{1}}(3.43)$

Infinite parallel plate capacitor

Write $\sigma_{\alpha\beta}$ .

$\begin{aligned}\mathbf{B} &= 0 \\ \mathbf{E} &= - \frac{\sigma}{\epsilon_0} \mathbf{e}_z\end{aligned} \hspace{\stretch{1}}(4.44)$

FIXME: derive this. Observe that we have no distance dependence in the field because it is an infinite plate.

$\begin{aligned}\sigma_{1 1} &= \left( - \frac{1}{{2}} \delta^{1 1} \left( \frac{-\sigma}{\epsilon_0} \right)^2 \right) = - \frac{ \sigma^2}{ 2 \epsilon_0^2 } = \sigma_{22} \\ \sigma_{3 3} &= \left( (E^3)^2 - \frac{1}{{2}} \mathbf{E}^2 \right) = - \frac{1}{{2}} \mathbf{E}^2 = - \sigma_{2 2}\end{aligned} \hspace{\stretch{1}}(4.46)$

Force per unit area is then

$\begin{aligned}f_\alpha &= n_\beta \sigma_{\alpha \beta} \\ &= n_3 \sigma_{\alpha 3}\end{aligned}$

$\begin{aligned}f_1 &= 0 = f_2 \\ f_3 &= \sigma_{3 3} = -\frac{\sigma^2}{2 \epsilon_0^2}\end{aligned} \hspace{\stretch{1}}(4.48)$

$\begin{aligned}\mathbf{f} = -\frac{\sigma^2}{2 \epsilon_0^2} \mathbf{e}_z\end{aligned} \hspace{\stretch{1}}(4.50)$

REMEMBER: EXAM WEDNESDAY!

References

[1] L.D. Landau and E.M. Lifshitz. The classical theory of fields. Butterworth-Heinemann, 1980.

[2] Wikipedia. Angle of incidence — wikipedia, the free encyclopedia [online]. 2011. [Online; accessed 11-April-2011]. http://en.wikipedia.org/w/index.php?title=Angle_of_incidence&oldid=421647114.

Posted in Math and Physics Learning. | Tagged: electromagnetic force, energy momentum tensor, PHY450, radiation reflection, stress energy tensor | Leave a Comment »

« Previous Entries

	Determining the alig… on C structure alignment pad…
	Manas shetty on Cartesian to spherical change…
	peeterjoot on Derivative recurrence relation…
	Daniel Pires on Derivative recurrence relation…
	peeterjoot on Curious problem using the vari…

Math, physics, perl, and programming obscurity.

Categories

Archives

Recent Posts

Meta

Recent Comments

People not reading this blog: 7,179,979,522 minus:

Subscribe

Posts Tagged ‘PHY450’

Reading.

Radiation reaction force.

Example: our dipole system

Limits of classical electrodynamics.

References

Charged particle in a circle without Geometric Algebra.

References

Charged particle in a circle.

The potentials.

General fields for this system.

An approximation near the center.

Collision of photon and electron.

Pion decay.

Reading.

Fields from the Lienard-Wiechert potentials

Check. Particle at rest.

Check. Particle moving with constant velocity.

Back to extracting physics from the Lienard-Wiechert field equations

References

Reading.

Recap.

Incorporating radiation effects as a friction term.

References

HW6. Question 3. (Non subtle hints about how important this is (i.e. for the exam)

Motivation.

On the signs of the force per unit area

Returning to the tutorial notes

Working out the tensor.

Aside: On the geometry, and the angle of incidence.

Back to the problem (again).

Force per unit area?

A problem from Griffiths.

Infinite parallel plate capacitor

References