[Click here for a PDF of this post with nicer formatting]
Disclaimer
This is an ungraded set of answers to the problems posed.
Question: Sackur-Tetrode entropy of an Ideal Gas
The entropy of an ideal gas is given by

Find the temperature of this gas via  . Find the energy per particle at which the entropy becomes negative. Is there any meaning to this temperature?
. Find the energy per particle at which the entropy becomes negative. Is there any meaning to this temperature?
Answer
Taking derivatives we find

or

The energies for which the entropy is negative are given by

or

In terms of the temperature  this negative entropy condition is given by
this negative entropy condition is given by

or

There will be a particle density  for which this distance
for which this distance  will start approaching the distance between atoms. This distance constrains the validity of the ideal gas law entropy equation. Putting this quantity back into the entropy eq. 1.1.1 we have
will start approaching the distance between atoms. This distance constrains the validity of the ideal gas law entropy equation. Putting this quantity back into the entropy eq. 1.1.1 we have

We see that a positive entropy requirement puts a bound on this distance (as a function of temperature) since we must also have

for the gas to be in the classical domain. I’d actually expect a gas to liquefy before this transition point, making such a low temperature nonphysical. To get a feel for whether this is likely the case, we should expect that the logarithm argument to be

at the point where gasses liquefy (at which point we assume the ideal gas law is no longer accurate) to be well above unity. Checking this for 1 liter of a gas with  atoms for hydrogen, helium, and neon respectively we find the values for eq. 1.1.10 are
atoms for hydrogen, helium, and neon respectively we find the values for eq. 1.1.10 are

At least for these first few cases we see that the ideal gas law has lost its meaning well before the temperatures below which the entropy would become negative.
Question: Ideal gas thermodynamics
An ideal gas starts at  in the pressure-volume diagram (x-axis =
in the pressure-volume diagram (x-axis = 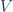 , y-axis =
, y-axis =  ), then moves at constant pressure to a larger volume
), then moves at constant pressure to a larger volume  , then moves to a larger pressure at constant volume to
, then moves to a larger pressure at constant volume to  , and finally returns to
, and finally returns to  , thus undergoing a cyclic process (forming a triangle in
, thus undergoing a cyclic process (forming a triangle in  plane). For each step, find the work done on the gas, the change in energy content, and heat added to the gas. Find the total work/energy/heat change over the entire cycle.
plane). For each step, find the work done on the gas, the change in energy content, and heat added to the gas. Find the total work/energy/heat change over the entire cycle.
Answer
Our process is illustrated in fig. 1.1.

Fig 1.1: Cyclic pressure volume process
Step 1
This problem is somewhat underspecified. From the ideal gas law, regardless of how the gas got from the initial to the final states, we have


So a volume increase with fixed  implies that there is a corresponding increase in
implies that there is a corresponding increase in  . We could have for example, an increase in the number of particles, as in the evaporation process illustrated of fig. 1.2, where a piston held down by (fixed) atmospheric pressure is pushed up as the additional gas boils off.
. We could have for example, an increase in the number of particles, as in the evaporation process illustrated of fig. 1.2, where a piston held down by (fixed) atmospheric pressure is pushed up as the additional gas boils off.

Fig 1.2: Evaporation process under (fixed) atmospheric pressure
Alternately, we could have a system such as that of fig. 1.3, with a fixed amount of gas is in contact with a heat source that supplies the energy required to induce the required increase in temperature.

Fig 1.3: Gas of fixed mass absorbing heat
Regardless of the source of the energy that accounts for the increase in volume the work done on the gas (a negation of the positive work the gas is performing on the system, perhaps a piston as in the picture) is

Let’s now assume that we have the second sort of configuration above, where the total amount of gas is held fixed. From the ideal gas relations of eq. 1.0.12.12, and with  ,
,  , and
, and  , we have
, we have

The change in energy of the ideal gas, assuming three degrees of freedom, is

The energy balance then requires that the total heat absorbed by the gas must include that portion that has done work on the system, plus the excess kinetic energy of the gas. That is

Step 2
For this leg of the cycle we have no work done on the gas

We do, however have a change in energy. The energy of the gas is

With  , the change of energy of the gas, the total heat absorbed by the gas, is
, the change of energy of the gas, the total heat absorbed by the gas, is

Step 3
For the final leg of the cycle, the work done on the gas is

This is positive this time
Unlike the first part of the cycle, the work done on the gas is positive this time (work is being done on the gas to both compress it). The change in energy of the gas, however, is negative, with the difference between final and initial energy being

The simultaneous compression and the pressure reduction require energy to be removed from the gas. We must have a negative change in heat  , with heat emitted in this phase of the cycle. This can be verified explicitly
, with heat emitted in this phase of the cycle. This can be verified explicitly

Changes over the complete cycle.
Summarizing the results from each of the phases, we have









Summing the changes in the work we have

This is the area of the triangle, as expected. Since it is positive, there is net work done on the gas.
We expect the energy changes to sum to zero, and this can be verified explicitly finding

With net work done on the gas and no change in energy, there should be no net heat absorption by the gas, with a total change in heat that should equal, in amplitude, the total work done on the gas. This is confirmed by summation

Question: Adiabatic process for an Ideal Gas
Show that when an ideal monoatomic gas expands adiabatically, the temperature and pressure are related by

Answer
From (3.34b) of [1], we find that the Adiabatic condition can be expressed algebraically as

With

this is

Dividing through by  , this becomes a perfect differential, and we can integrate
, this becomes a perfect differential, and we can integrate

Exponentiating yields

The desired relation follows by taking derivatives

or

as desired.
References
[1] C. Kittel and H. Kroemer. Thermal physics. WH Freeman, 1980.





















