Peeter Joot's (OLD) Blog.

Math, physics, perl, and programming obscurity.

Archive for January, 2012

« Previous Entries

PHY454H1S Continuum Mechanics. Lecture 6: Compatibility condition and elastostatics. Taught by Prof. K. Das.

Posted by peeterjoot on January 29, 2012

[Click here for a PDF of this post with nicer formatting and figures if the post had any (especially if my latex to wordpress script has left FORMULA DOES NOT PARSE errors.)]

Disclaimer.

Peeter’s lecture notes from class. May not be entirely coherent.

Review: Elastostatics

We’ve defined the strain tensor, where assuming the second order terms are ignored, was

\begin{aligned}e_{ij} = \frac{1}{{2}} \left( \frac{\partial {e_i}}{\partial {x_j}}+ \frac{\partial {e_j}}{\partial {x_i}} \right).\end{aligned} \hspace{\stretch{1}}(2.1)

We’ve also defined a stress tensor defined implicitly as a divergence relationship using the force per unit volume F_i in direction i

\begin{aligned}\sigma_{ij} \leftrightarrow F_i = \frac{\partial {\sigma_{ij}}}{\partial {x_j}}.\end{aligned} \hspace{\stretch{1}}(2.2)

We’ve also discussed the constitutive relation, relating stress \sigma_{ij} and strain e_{ij}.

We’ve also discussed linear constitutive relationships (Hooke’s law).

2D strain.

\begin{aligned}e_{ij} = \begin{bmatrix}e_{11} & e_{12} \\ e_{21} & e_{22}\end{bmatrix}\end{aligned} \hspace{\stretch{1}}(3.3)

From 2.1 we see that we have

\begin{aligned}e_{11} &= \frac{\partial {e_1}}{\partial {x_1}} \\ e_{22} &= \frac{\partial {e_2}}{\partial {x_2}} \\ e_{12} = e_{21} &= \frac{1}{{2}} \left( \frac{\partial {e_2}}{\partial {x_1}}+ \frac{\partial {e_1}}{\partial {x_2}} \right).\end{aligned} \hspace{\stretch{1}}(3.4)

We have a relationship between these displacements (called the compatibility relationship), which is

\begin{aligned}\boxed{\frac{\partial^2 {{e_{11}}}}{\partial {{x_2}}^2} +\frac{\partial^2 {{e_{22}}}}{\partial {{x_1}}^2} = 2\frac{\partial^2 e_{12}}{\partial x_1 \partial x_2}.}\end{aligned} \hspace{\stretch{1}}(3.7)

We find this by straight computation

\begin{aligned}\frac{\partial^2 {{e_{11}}}}{\partial {{x_2}}^2} &= \frac{\partial^2 {{}}}{\partial {{x_2}}^2}\left( \frac{\partial {e_1}}{\partial {x_1}}\right) \\ &=\frac{\partial^3 e_1}{\partial x_1 \partial x_2^2},\end{aligned}

and

\begin{aligned}\frac{\partial^2 {{e_{22}}}}{\partial {{x_1}}^2} &= \frac{\partial^2 {{}}}{\partial {{x_1}}^2}\left( \frac{\partial {e_2}}{\partial {x_2}}\right) \\ &= \frac{\partial^3 e_2}{\partial x_2 \partial x_1^2},\end{aligned}

Now, looking at the cross term we find

\begin{aligned}2 \frac{\partial^2 e_{12}}{\partial x_1 \partial x_2} &= \frac{\partial^2 e_{12}}{\partial x_1 \partial x_2} \left(\frac{\partial {e_2}}{\partial {x_1}}+ \frac{\partial {e_1}}{\partial {x_2}} \right) \\ &=\left(\frac{\partial^3 e_1}{\partial x_1 \partial x_2^2} +\frac{\partial^3 e_2}{\partial x_2 \partial x_1^2} \right) \\ &=\frac{\partial^2 {{e_{22}}}}{\partial {{x_1}}^2} +\frac{\partial^2 {{e_{11}}}}{\partial {{x_2}}^2} \end{aligned}

This is called the compatibility condition, and ensures that we don’t have a disjoint deformation of the form in figure (\ref{fig:continuumL6:continuumL6fig1})

\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{continuumL6fig1}
\caption{disjoint deformation illustrated.}
\end{figure}

3D strain.

While we have 9 components in the tensor, not all of these are independent. The sets above and below the diagonal can be related, as illustrated in figure (\ref{fig:continuumL6:continuumL6fig2}).

\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{continuumL6fig2}
\caption{continuumL6fig2}
\end{figure}

Here we have 6 relationships between the components of the strain tensor e_{ij}. Deriving these will be assigned in the homework.

Elastodynamics. Elastic waves.

Reading: Chapter III (section 22 – section 26) of the text [1].

Example: sound or water waves (i.e. waves in a solid or liquid material that comes back to its original position.)

\begin{definition}
\emph{(Elastic Wave)}

An elastic wave is a type of mechanical wave that propagates through or on the surface of a medium. The elasticity of the material provides the restoring force (that returns the material to its original state). The displacement and the restoring force are assumed to be linearly related.
\end{definition}

In symbols we say

\begin{aligned}e_i(x_j, t) \quad \mbox{related to force},\end{aligned} \hspace{\stretch{1}}(5.8)

and specifically

\begin{aligned}\rho \frac{\partial^2 {{e_i}}}{\partial {{t}}^2} = F_i = \frac{\partial {\sigma_{ij}}}{\partial {x_j}}.\end{aligned} \hspace{\stretch{1}}(5.9)

This is just Newton’s second law, F = ma, but expressed in terms of a unit volume.

Should we have an external body force (per unit volume) f_i acting on the body then we must modify this, writing

\begin{aligned}\boxed{\rho \frac{\partial^2 {{e_i}}}{\partial {{t}}^2} = \frac{\partial {\sigma_{ij}}}{\partial {x_j}} + f_i}\end{aligned} \hspace{\stretch{1}}(5.10)

Note that we are separating out the “original” forces that produced the stress and strain on the object from any constant external forces that act on the body (i.e. a gravitational field).

With

\begin{aligned}e_{ij} = \frac{1}{{2}} \left( \frac{\partial {e_i}}{\partial {x_j}}+ \frac{\partial {e_j}}{\partial {x_i}} \right),\end{aligned} \hspace{\stretch{1}}(5.11)

we can expand the stress divergence, for the case of homogeneous deformation, in terms of the Lam\’e parameters

\begin{aligned}\sigma_{ij} = \lambda e_{kk} \delta_{ij} + 2 \mu e_{ij}.\end{aligned} \hspace{\stretch{1}}(5.12)

We compute

\begin{aligned}\frac{\partial {\sigma_{ij}}}{\partial {x_j}}&=\lambda \frac{\partial {e_{kk}}}{\partial {x_j}}\delta_{ij} + 2 \mu \frac{\partial {}}{\partial {x_j}}\frac{1}{{2}} \left( \frac{\partial {e_i}}{\partial {x_j}}+ \frac{\partial {e_j}}{\partial {x_i}} \right), \\ &=\lambda \frac{\partial {e_{kk}}}{\partial {x_i}}+ \mu \left(\frac{\partial^2 {{e_{i}}}}{\partial {{x_j}}^2}+\frac{\partial^2 e_{j} }{ \partial x_j \partial x_i}\right) \\ &=\lambda \frac{\partial {}}{\partial {x_i}}\frac{\partial {e_k}}{\partial {x_k}}+ \mu \left(\frac{\partial^2 {{e_{i}}}}{\partial {{x_j}}^2}+\frac{\partial^2 e_{k} }{ \partial x_k \partial x_i}\right) \\ &=(\lambda + \mu)\frac{\partial {}}{\partial {x_i}}\frac{\partial {e_k}}{\partial {x_k}}+ \mu \frac{\partial^2 {{e_{i}}}}{\partial {{x_j}}^2}\end{aligned}

We find, for homogeneous deformations, that the force per unit volume on our element of mass, in the absence of external forces (the body forces), takes the form

\begin{aligned}\rho \frac{\partial^2 {{e_i}}}{\partial {{t}}^2} = (\lambda + \mu) \frac{\partial^2 e_i}{\partial x_i \partial x_j}+ \mu\frac{\partial^2 e_i}{\partial x_j^2}.\end{aligned} \hspace{\stretch{1}}(5.13)

This can be seen to be equivalent to the vector relationship

\begin{aligned}\boxed{\rho \frac{\partial^2 {\mathbf{e}}}{\partial {{t}}^2} = (\lambda + \mu) \boldsymbol{\nabla} (\boldsymbol{\nabla} \cdot \mathbf{e}) + \mu \boldsymbol{\nabla}^2 \mathbf{e}.}\end{aligned} \hspace{\stretch{1}}(5.14)

TODO: What form do the stress and strain tensors take in vector form?

References

[1] L.D. Landau, EM Lifshitz, JB Sykes, WH Reid, and E.H. Dill. Theory of elasticity: Vol. 7 of course of theoretical physics. 1960.

Posted in Math and Physics Learning. | Tagged: , , , , , , , , | Leave a Comment »

PHY454H1S Continuum Mechanics. Lecture 5: Constitutive relationship. Taught by Prof. K. Das.

Posted by peeterjoot on January 28, 2012

[Click here for a PDF of this post with nicer formatting and figures if the post had any (especially if my latex to wordpress script has left FORMULA DOES NOT PARSE errors.)]

Disclaimer.

Peeter’s lecture notes from class. May not be entirely coherent.

Review: Cauchy Tetrahedron.

Referring to figure (\ref{fig:continuumL5:continuumL5fig1})
\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{continuumL5fig1}
\caption{Cauchy tetrahedron direction cosines.}
\end{figure}

recall that we can decompose our force into components that refer to our direction cosines n_i = \cos\phi_i

\begin{aligned}f_1 &= \sigma_{11} n_1 + \sigma_{12} n_2 + \sigma_{13} n_3 \\ f_2 &= \sigma_{21} n_1 + \sigma_{22} n_2 + \sigma_{23} n_3 \\ f_3 &= \sigma_{31} n_1 + \sigma_{32} n_2 + \sigma_{33} n_3\end{aligned} \hspace{\stretch{1}}(2.1)

Or in tensor form

\begin{aligned}f_i = \sigma_{ij} n_j.\end{aligned} \hspace{\stretch{1}}(2.4)

We call this the traction vector and denote it in vector form as

\begin{aligned}\mathbf{T} = \boldsymbol{\sigma} \cdot \hat{\mathbf{n}}=\begin{bmatrix}\sigma_{11} & \sigma_{12} & \sigma_{13} \\ \sigma_{21} & \sigma_{22} & \sigma_{23} \\ \sigma_{31} & \sigma_{32} & \sigma_{33}\end{bmatrix}\begin{bmatrix}n_1 \\ n_2 \\ n_3\end{bmatrix}\end{aligned} \hspace{\stretch{1}}(2.5)

Constitutive relation.

Reading: section 2, section 4 and section 5 from the text [1].

We can find the relationship between stress and strain, both analytically and experimentally, and call this the Constitutive relation. We prefer to deal with ranges of distortion that are small enough that we can make a linear approximation for this relation. In general such a linear relationship takes the form

\begin{aligned}\sigma_{ij} = c_{ijkl} e_{kl}.\end{aligned} \hspace{\stretch{1}}(3.6)

Consider the number of components that we are talking about for various rank tensors

\begin{aligned}\begin{array}{l l}\mbox{latex 0^\text{th}$ rank tensor} & \mbox{3^0 = 1 components} \\ \mbox{1^\text{st} rank tensor} & \mbox{3^1 = 3 components} \\ \mbox{2^\text{nd} rank tensor} & \mbox{3^2 = 9 components} \\ \mbox{3^\text{rd} rank tensor} & \mbox{3^3 = 81 components}\end{array}\end{aligned} \hspace{\stretch{1}}(3.7)$

We have a lot of components, even for a linear relation between stress and strain. For isotropic materials we model the constitutive relation instead as

\begin{aligned}\boxed{\sigma_{ij} = \lambda e_{kk} \delta_{ij} + 2 \mu e_{ij}.}\end{aligned} \hspace{\stretch{1}}(3.8)

For such a modeling of the material the (measured) values \lambda and \mu (shear modulus or modulus of rigidity) are called the Lam\’e parameters.

It will be useful to compute the trace of the stress tensor in the form of the constitutive relation for the isotropic model. We find

\begin{aligned}\sigma_{ii}&= \lambda e_{kk} \delta_{ii} + 2 \mu e_{ii} \\ &= 3 \lambda e_{kk} + 2 \mu e_{jj},\end{aligned}

or

\begin{aligned}\sigma_{ii} = (3 \lambda + 2 \mu) e_{kk}.\end{aligned} \hspace{\stretch{1}}(3.9)

We can now also invert this, to find the trace of the strain tensor in terms of the stress tensor

\begin{aligned}e_{ii} = \frac{\sigma_{kk}}{3 \lambda + 2 \mu}\end{aligned} \hspace{\stretch{1}}(3.10)

Substituting back into our original relationship 3.8, and find

\begin{aligned}\sigma_{ij} = \lambda \frac{\sigma_{kk}}{3 \lambda + 2 \mu} \delta_{ij} + 2 \mu e_{ij},\end{aligned} \hspace{\stretch{1}}(3.12)

which finally provides an inverted expression with the strain tensor expressed in terms of the stress tensor

\begin{aligned}\boxed{2 \mu e_{ij} =\sigma_{ij} - \lambda \frac{\sigma_{kk}}{3 \lambda + 2 \mu} \delta_{ij}.}\end{aligned} \hspace{\stretch{1}}(3.12)

Special cases.

Hydrostatic compression

Hydrostatic compression is when we have no shear stress, only normal components of the stress matrix \sigma_{ij} is nonzero. Strictly speaking we define Hydrostatic compression as

\begin{aligned}\sigma_{ij} = -p \delta_{ij},\end{aligned} \hspace{\stretch{1}}(3.13)

i.e. not only diagonal, but with all the components of the stress tensor equal.

We can write the trace of the stress tensor as

\begin{aligned}\sigma_{ii} = - 3 p = (3 \lambda + 2 \mu) e_{kk}.\end{aligned} \hspace{\stretch{1}}(3.14)

Now, from our discussion of the strain tensor e_{ij} recall that we found in the limit

\begin{aligned}dV' = (1 + e_{ii}) dV,\end{aligned} \hspace{\stretch{1}}(3.15)

allowing us to express the change in volume relative to the original volume in terms of the strain trace

\begin{aligned}e_{ii} = \frac{dV' - dV}{dV}.\end{aligned} \hspace{\stretch{1}}(3.16)

Writing that relative volume difference as \Delta V/V we find

\begin{aligned}- 3 p = (3 \lambda + 2 \mu) \frac{\Delta V}{V},\end{aligned} \hspace{\stretch{1}}(3.17)

or

\begin{aligned}- \frac{ p V}{\Delta V} = \left( \lambda + \frac{2}{3} \mu \right) = K,\end{aligned} \hspace{\stretch{1}}(3.18)

where K is called the Bulk modulus.

Uniaxial stress

Again illustrated in the plane as in figure (\ref{fig:continuumL5:continuumL5fig2})
\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{continuumL5fig2}
\caption{Uniaxial stress.}
\end{figure}

Expanding out 3.12 we have for the 1,1 element of the strain tensor

\begin{aligned}\boldsymbol{\sigma} =\begin{bmatrix}\sigma_{11} & 0 & 0\\ 0 & 0 & 0 \\ 0 & 0 & 0\end{bmatrix}\end{aligned} \hspace{\stretch{1}}(3.19)

\begin{aligned}2 \mu e_{11}&= \sigma_{11} - \frac{\lambda ( \sigma_{11} + \not{{\sigma_{22}}} ) }{3 \lambda + 2 \mu} \\ &= \sigma_{11} \frac{3 \lambda + 2 \mu - \lambda }{3 \lambda + 2 \mu} \\ &= 2 \sigma_{11} \frac{\lambda + \mu }{3 \lambda + 2 \mu}\end{aligned}

or

\begin{aligned}\frac{\sigma_{11}}{e_{11}} = \frac{\mu(3 \lambda + 2 \mu)}{\lambda + \mu } = E\end{aligned} \hspace{\stretch{1}}(3.20)

where E is Young’s modulus. Young’s modulus in the text (5.3) is given in terms of the bulk modulus K. Using \lambda = K - 2\mu/3 we find

\begin{aligned}E &=\frac{\mu(3 \lambda + 2 \mu)}{\lambda + \mu } \\ &=\frac{\mu(3 (K - 2\mu/3)+ 2 \mu)}{K - 2\mu/3 + \mu } \\ &=\frac{3 K \mu}{ K + \mu/3 } \end{aligned}

\begin{aligned}\boxed{E =\frac{\mu(3 \lambda + 2 \mu)}{\lambda + \mu } =\frac{9 K \mu}{ 3 K + \mu } }\end{aligned} \hspace{\stretch{1}}(3.21)

FIXME: figure (\ref{fig:continuumL5:continuumL5fig3}) reference?

\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{continuumL5fig3}
\caption{stress associated with Young’s modulus}
\end{figure}

We define Poisson’s ratio \nu as the quantity

\begin{aligned}\frac{e_{22}}{e_{11}} = \frac{e_{33}}{e_{11}} = - \nu.\end{aligned} \hspace{\stretch{1}}(3.22)

Note that we are still talking about uniaxial stress here. Referring back to 3.12 we have

\begin{aligned}2 \mu e_{2 2}&= \sigma_{2 2} - \lambda \frac{\sigma_{k k}}{3 \lambda + 2 \mu} \delta_{2 2} \\ &= \sigma_{2 2} - \lambda \frac{\sigma_{k k}}{3 \lambda + 2 \mu} \\ &= - \frac{\lambda \sigma_{11}}{3 \lambda + 2 \mu}\end{aligned}

Recall (3.20) that we had

\begin{aligned}\sigma_{11} = \frac{\mu (3 \lambda + 2 \mu)}{\lambda + \mu} e_{11}.\end{aligned} \hspace{\stretch{1}}(3.23)

Inserting this gives us

\begin{aligned}2 \mu e_{22} = - \frac{\lambda}{\not{{3 \lambda + 2 \mu}}} \frac{ \mu (\not{{3 \lambda + 2\mu}})}{\lambda + \mu} e_{11}\end{aligned}

so

\begin{aligned}\boxed{\nu = -\frac{e_{22}}{e_{11}} = \frac{\lambda}{2 (\lambda + \mu)}.}\end{aligned} \hspace{\stretch{1}}(3.24)

We can also relate the Poisson’s ratio \nu to the shear modulus \mu

\begin{aligned}\mu = \frac{E}{2(1 + \nu)}\end{aligned} \hspace{\stretch{1}}(3.25)

\begin{aligned}\lambda = \frac{E \nu}{(1 - 2 \nu)(1 + \mu)}\end{aligned} \hspace{\stretch{1}}(3.26)

\begin{aligned}e_{11} &= \frac{1}{{E}}\left( \sigma_{11} - \nu(\sigma_{22} + \sigma_{33}) \right) \\ e_{22} &= \frac{1}{{E}}\left( \sigma_{22} - \nu(\sigma_{11} + \sigma_{33}) \right) \\ e_{33} &= \frac{1}{{E}}\left( \sigma_{33} - \nu(\sigma_{11} + \sigma_{22}) \right)\end{aligned} \hspace{\stretch{1}}(3.27)

These ones are (5.14) in the text, and are easy enough to verify (not done here).

Appendix. Computing the relation between Poisson’s ratio and shear modulus.

Young’s modulus is given in 3.21 (equation (43) in the Professor’s notes) as

\begin{aligned}E = \frac{\mu(3 \lambda + 2 \mu)}{\lambda + \mu },\end{aligned} \hspace{\stretch{1}}(3.30)

and for Poisson’s ratio 3.24 (equation (46) in the Professor’s notes) we have

\begin{aligned}\nu = -\frac{e_{22}}{e_{11}} = \frac{\lambda}{2 (\lambda + \mu)}.\end{aligned} \hspace{\stretch{1}}(3.31)

Let’s derive the other stated relationships (equation (47) in the Professor’s notes). I get

\begin{aligned}2 (\lambda + \mu) \nu = \lambda \\ \implies \\ \lambda ( 2 \nu - 1 ) = - 2\mu\nu\end{aligned}

or

\begin{aligned}\lambda = \frac{ 2 \mu \nu} { 1 - 2 \nu }\end{aligned}

For substitution into the Young’s modulus equation calculate

\begin{aligned}\lambda + \mu &= \frac{ 2 \mu \nu} { 1 - 2 \nu } + \mu \\ &= \mu \left( \frac{ 2 \nu} { 1 - 2 \nu } + 1 \right) \\ &= \mu \frac{ 2 \nu + 1 - 2 \nu} { 1 - 2 \nu } \\ &= \frac{ \mu} { 1 - 2 \nu } \\ \end{aligned}

and

\begin{aligned}3 \lambda + 2 \mu &= 3 \frac{ \mu} { 1 - 2 \nu } - \mu \\ &= \mu \frac{ 3 - (1 - 2 \nu)} { 1 - 2 \nu } \\ &= \mu \frac{ 2 + 2 \nu} { 1 - 2 \nu } \\ &= 2 \mu \frac{ 1 + \nu} { 1 - 2 \nu } \\ \end{aligned}

Putting these together we find

\begin{aligned}E &= \frac{\mu(3 \lambda + 2 \mu)}{\lambda + \mu } \\ &= \mu 2 \mu \frac{ 1 + \nu} { 1 - 2 \nu } \frac{ 1 - 2 \nu}{\mu} \\ &= 2 \mu ( 1 + \nu ) \\ \end{aligned}

Rearranging we have

\begin{aligned}\mu = \frac{E}{2 (1 + \nu)}.\end{aligned} \hspace{\stretch{1}}(3.32)

This matches (5.9) in the text (where \sigma is used instead of \nu).

We also find

\begin{aligned}\lambda &= \frac{ 2 \mu \nu} { 1 - 2 \nu } \\ &= \frac{ \nu} { 1 - 2 \nu } \frac{E }{1 + \nu}.\end{aligned}

References

[1] L.D. Landau, EM Lifshitz, JB Sykes, WH Reid, and E.H. Dill. Theory of elasticity: Vol. 7 of course of theoretical physics. 1960.

Posted in Math and Physics Learning. | Tagged: , , , , , , , , , , , , , , | Leave a Comment »

Infinitesimal rotations

Posted by peeterjoot on January 27, 2012

[Click here for a PDF of this post with nicer formatting and figures if the post had any (especially if my latex to wordpress script has left FORMULA DOES NOT PARSE errors.)]

Motivation.

In a classical mechanics lecture (which I audited) Prof. Poppitz made the claim that an infinitesimal rotation in direction \hat{\mathbf{n}} of magnitude \delta \phi has the form

\begin{aligned}\mathbf{x} \rightarrow \mathbf{x} + \delta \boldsymbol{\phi} \times \mathbf{x},\end{aligned} \hspace{\stretch{1}}(1.1)

where

\begin{aligned}\delta \boldsymbol{\phi} = \hat{\mathbf{n}} \delta \phi.\end{aligned} \hspace{\stretch{1}}(1.2)

I believe he expressed things in terms of the differential displacement

\begin{aligned}\delta \mathbf{x} = \delta \boldsymbol{\phi} \times \mathbf{x}\end{aligned} \hspace{\stretch{1}}(1.3)

This was verified for the special case \hat{\mathbf{n}} = \hat{\mathbf{z}} and \mathbf{x} = x \hat{\mathbf{x}}. Let’s derive this in the general case too.

With geometric algebra.

Let’s temporarily dispense with the normal notation and introduce two perpendicular unit vectors \hat{\mathbf{u}}, and \hat{\mathbf{v}} in the plane of the rotation. Relate these to the unit normal with

\begin{aligned}\hat{\mathbf{n}} = \hat{\mathbf{u}} \times \hat{\mathbf{v}}.\end{aligned} \hspace{\stretch{1}}(2.4)

A rotation through an angle \phi (infinitesimal or otherwise) is then

\begin{aligned}\mathbf{x} \rightarrow e^{-\hat{\mathbf{u}} \hat{\mathbf{v}} \phi/2} \mathbf{x} e^{\hat{\mathbf{u}} \hat{\mathbf{v}} \phi/2}.\end{aligned} \hspace{\stretch{1}}(2.5)

Suppose that we decompose \mathbf{x} into components in the plane and in the direction of the normal \hat{\mathbf{n}}. We have

\begin{aligned}\mathbf{x} = x_u \hat{\mathbf{u}} + x_v \hat{\mathbf{v}} + x_n \hat{\mathbf{n}}.\end{aligned} \hspace{\stretch{1}}(2.6)

The exponentials commute with the \hat{\mathbf{n}} vector, and anticommute otherwise, leaving us with

\begin{aligned}\mathbf{x} &\rightarrow x_n \hat{\mathbf{n}} + (x_u \hat{\mathbf{u}} + x_v \hat{\mathbf{v}}) e^{\hat{\mathbf{u}} \hat{\mathbf{v}} \phi} \\ &=x_n \hat{\mathbf{n}} + (x_u \hat{\mathbf{u}} + x_v \hat{\mathbf{v}}) (\cos\phi + \hat{\mathbf{u}} \hat{\mathbf{v}} \sin\phi) \\ &=x_n \hat{\mathbf{n}} + \hat{\mathbf{u}} (x_u \cos\phi - x_v \sin\phi) +\hat{\mathbf{v}} (x_v \cos\phi + x_u \sin\phi).\end{aligned}

In the last line we use \hat{\mathbf{u}}^2 = 1 and \hat{\mathbf{u}} \hat{\mathbf{v}} = - \hat{\mathbf{v}} \hat{\mathbf{u}}. Making the angle infinitesimal \phi \rightarrow \delta \phi we have

\begin{aligned}\mathbf{x} &\rightarrow x_n \hat{\mathbf{n}} + \hat{\mathbf{u}} (x_u - x_v \delta\phi) +\hat{\mathbf{v}} (x_v + x_u \delta\phi) \\ &=\mathbf{x} + \delta\phi( x_u \hat{\mathbf{v}} - x_v \hat{\mathbf{u}})\end{aligned}

We have only to confirm that this matches the assumed cross product representation

\begin{aligned}\hat{\mathbf{n}} \times \mathbf{x}&=\begin{vmatrix}\hat{\mathbf{u}} & \hat{\mathbf{v}} & \hat{\mathbf{n}} \\ 0 & 0 & 1 \\ x_u & x_v & x_n\end{vmatrix} \\ &=-\hat{\mathbf{u}} x_v + \hat{\mathbf{v}} x_u\end{aligned}

Taking the two last computations we find

\begin{aligned}\delta \mathbf{x} = \delta \phi \hat{\mathbf{n}} \times \mathbf{x} = \delta \boldsymbol{\phi} \times \mathbf{x},\end{aligned} \hspace{\stretch{1}}(2.7)

as desired.

Without geometric algebra.

We’ve also done the setup above to verify this result without GA. Here we wish to apply the rotation to the coordinate vector of \mathbf{x} in the \{\hat{\mathbf{u}}, \hat{\mathbf{v}}, \hat{\mathbf{n}}\} basis which gives us

\begin{aligned}\begin{bmatrix}x_u \\ x_v \\ x_n \end{bmatrix}&\rightarrow \begin{bmatrix}\cos\delta\phi & -\sin\delta\phi & 0 \\ \sin\delta\phi & \cos\delta\phi & 0 \\ 0 & 0 & 1\end{bmatrix}\begin{bmatrix}x_u \\ x_v \\ x_n \end{bmatrix} \\ &\approx\begin{bmatrix}1 & -\delta\phi & 0 \\ \delta\phi & 1 & 0 \\ 0 & 0 & 1\end{bmatrix}\begin{bmatrix}x_u \\ x_v \\ x_n \end{bmatrix} \\ &=\begin{bmatrix}x_u \\ x_v \\ x_n \end{bmatrix} +\begin{bmatrix}0 & -\delta\phi & 0 \\ \delta\phi & 0 & 0 \\ 0 & 0 & 0\end{bmatrix}\begin{bmatrix}x_u \\ x_v \\ x_n \end{bmatrix} \\ &=\begin{bmatrix}x_u \\ x_v \\ x_n \end{bmatrix} +\delta\phi\begin{bmatrix}-x_v \\ x_u \\ 0\end{bmatrix} \end{aligned}

But as we’ve shown, this last coordinate vector is just \hat{\mathbf{n}} \times \mathbf{x}, and we get our desired result using plain old fashioned matrix algebra as well.

Really the only difference between this and what was done in class is that there’s no assumption here that \mathbf{x} = x \hat{\mathbf{x}}.

Posted in Math and Physics Learning. | Tagged: , , , , , , , , | Leave a Comment »

no such thing as ia64 fetchadd1.acq?

Posted by peeterjoot on January 26, 2012

Looking in the ia64 assembly reference, I see that we have only a fetchadd4 and fetchadd8 instruction, and unlike cmpxchg we don’t have 2 and 1 byte versions of this instruction.

I’d be curious to know what the rationale for that choice was? It seems reasonable to me to be able to use an instruction like this to do an atomic set bit or clear bit operation.

Posted in C/C++ development and debugging. | Tagged: , , , | Leave a Comment »

Proof that the conservation of energy is wrong. Not!

Posted by peeterjoot on January 25, 2012

My dad asked me about a website that claims to have a proof that the conservation of energy is wrong. The author, as part of his argument asks

“what exactly has the kinetic energy of the second rocket’s two burns been transformed into?”

My response to my dad was:

There’s lots of things that the burns have been turned into. He demonstrates an impressive lack of understanding of not only physics, but chemistry. In the chemical reactions that expel the exhaust particles, there’s lots of heat and light produced, both of which carry out energy from the ship. The other thing that is glaringly obvious is that he doesn’t even consider the exhaust itself.

Rockets are a very primitive devices and they actually propel themselves by tossing bits of themselves out the back. You could do this if you could put yourself on a very frictionless surface, along with a very heavy mass. If you toss the mass in one direction, you’ll end up moving in the other direction because momentum of you plus the mass have to be conserved. Perhaps you could actually do this experiment. Get a big rock and a dolly and put the dolly on ice with you and the rock, and then toss the rock. You should move in the opposite direction. Rockets expel most of their mass doing this, with chemical reactions making that expelled mass move much faster so that they gain they momentum (in the opposite direction) of the exhaust they expel. It’s the rocket, plus its exhaust, plus all the light and heat changes that occur in the chemical reactions that have to be considered if you are looking at conservation of energy.

Basically, the guy who authored this page appears to be talking out of his ass.  I’d like to try the experiment that I outlined for my dad.  Since it is winter time, perhaps I could just put on my ice skates and find something big to throw in front of me.  I should move backwards a bit in response.

Posted in Math and Physics Learning. | Tagged: | 1 Comment »

Mathematica now has a stackexchange site.

Posted by peeterjoot on January 25, 2012

The mathematica stackexchange proposal went from it’s looking for committers phase, to closed beta, and now to public beta

http://mathematica.stackexchange.com/

Whether or not it ends up as a permanent stackexchange site will depend on what sort of usage it gets, so if you are an active mathematica users, here’s a chance to build up a useful community.

Posted in Math and Physics Learning. | Tagged: , , | Leave a Comment »

Strain tensor in spherical coordinates

Posted by peeterjoot on January 23, 2012

[Click here for a PDF of this post with nicer formatting and figures if the post had any (especially if my latex to wordpress script has left FORMULA DOES NOT PARSE errors.)]

Spherical tensor.

To perform the derivation in spherical coordinates we have some setup to do first, since we need explicit representations of all three unit vectors. The radial vector we can get easily by geometry and find the usual

\begin{aligned}\hat{\mathbf{r}} =\begin{bmatrix}\sin\theta \cos\phi \\ \sin\theta \sin\phi \\ \cos\theta\end{bmatrix}\end{aligned} \hspace{\stretch{1}}(3.61)

We can get \hat{\boldsymbol{\phi}} by geometrical intuition since it the plane unit vector at angle \phi rotated by \pi/2. That is

\begin{aligned}\hat{\boldsymbol{\phi}} =\begin{bmatrix}-\sin\phi \\ \cos\phi \\ 0\end{bmatrix}\end{aligned} \hspace{\stretch{1}}(3.62)

We can get \hat{\boldsymbol{\theta}} by utilizing the right handedness of the coordinates since

\begin{aligned}\hat{\boldsymbol{\phi}} \times \hat{\mathbf{r}} = \hat{\boldsymbol{\theta}}\end{aligned} \hspace{\stretch{1}}(3.63)

and find

\begin{aligned}\hat{\boldsymbol{\theta}} =\begin{bmatrix}\cos\theta \cos\phi \\ \cos\theta \sin\phi \\ -\sin\theta\end{bmatrix}\end{aligned} \hspace{\stretch{1}}(3.64)

That and some Mathematica brute force can be used to calculate the differential strain element, and we find

\begin{aligned}\begin{aligned}&d\mathbf{l}'^2 - d\mathbf{x}^2 \\ &=2 (dr)^2 \biggl(\frac{\partial u_r}{\partial r}+ \frac{1}{{2}}\frac{\partial u_m}{\partial r} \frac{\partial u_m}{\partial r}\biggr) \\ & + 2 r^2 (d\theta )^2 \biggl(\frac{1}{{r}} u_r + \frac{1}{{2r^2}}(u_r^2 + u_{\theta }^2) - \frac{1}{{r^2}} u_{\theta } \frac{\partial u_r}{\partial \theta }+ \left(\frac{1}{{r}} + \frac{1}{{r^2}}u_r\right) \frac{\partial u_{\theta }}{\partial \theta }+ \frac{1}{{2 r^2}} \frac{\partial u_m}{\partial \theta } \frac{\partial u_m}{\partial \theta }\biggr) \\ &+ 2 r^2 \sin^2\theta (d\phi )^2 \biggl( \frac{1}{{2 r^2 \sin^2\theta}} u_\phi^2+ \frac{1}{{2 r^2 }} u_{\theta }^2 \cot^2\theta+ \frac{1}{{r}} u_r+ \frac{1}{{2 r^2}} u_r^2+ \left(\frac{1}{{r}} + \frac{1}{{r^2}}u_r\right) u_{\theta } \cot\theta \\ &\qquad- \frac{1}{{r^2 \sin\theta}} u_{\phi } \frac{\partial u_r}{\partial \phi }- \frac{1}{{r^2 }} u_{\phi } \frac{\cos\theta}{\sin^2\theta} \frac{\partial u_{\theta }}{\partial \phi }+ \frac{1}{{r^2 }} \frac{\partial u_{\phi }}{\partial \phi } \left(u_{\theta } \frac{\cos\theta}{\sin^2\theta} + \left(r + u_r\right) \frac{1}{{\sin\theta}} \right)+ \frac{1}{{2 r^2 \sin^2\theta}} \frac{\partial u_m}{\partial \phi } \frac{\partial u_m}{\partial \phi }\biggr) \\ & + 2 dr r d\theta \biggl(- \frac{1}{{r}} u_{\theta }+ \frac{1}{{r}} \frac{\partial u_r}{\partial \theta }- \frac{1}{{r}} u_{\theta } \frac{\partial u_r}{\partial r}+ \frac{\partial u_{\theta }}{\partial r} \left(1 + \frac{u_r}{r} \right)+ \frac{1}{{r}} \frac{\partial u_m}{\partial r} \frac{\partial u_m}{\partial \theta }\biggr) \\ & + 2 r^2 \sin\theta d\theta d\phi \biggl(\frac{1}{{r^2 }} u_{\theta } u_{\phi }- \frac{1}{{r^2 \sin\theta}} u_{\theta } \frac{\partial u_r}{\partial \phi }- \frac{1}{{r^2 }} u_{\phi } \frac{\partial u_r}{\partial \theta }- \frac{1}{{r^2 }} u_{\phi } \cot\theta \left(r + u_r + \frac{\partial u_{\theta }}{\partial \theta }\right) \\ &\qquad+ \frac{1}{{r^2 \sin\theta}} \left(r + u_r \right) \frac{\partial u_{\theta }}{\partial \phi }+ \frac{\partial u_{\phi }}{\partial \theta } \left(\frac{u_{\theta }}{r^2} \cot\theta + \frac{1}{{r}} + \frac{u_r}{r^2} \right)+ \frac{1}{{r^2 \sin\theta}} \frac{\partial u_m}{\partial \theta } \frac{\partial u_m}{\partial \phi }\biggr) \\ & + 2 r \sin\theta d\phi dr \biggl(- \frac{1}{{r }} u_{\phi }+ \frac{1}{{r \sin\theta}} \frac{\partial u_r}{\partial \phi }- u_{\phi } \frac{1}{{r }} \frac{\partial u_r}{\partial r}- u_{\phi } \cot\theta \frac{1}{{r }} \frac{\partial u_{\theta }}{\partial r}+ \frac{1}{{r }} \frac{\partial u_{\phi }}{\partial r} \left( u_{\theta } \cot\theta + r + u_r \right)+ \frac{1}{{r \sin\theta}} \frac{\partial u_m}{\partial \phi } \frac{\partial u_m}{\partial r}\biggr)\end{aligned}\end{aligned} \hspace{\stretch{1}}(3.65)

A manual derivation.

Doing the calculation pretty much completely with Mathematica is rather unsatisfying. To set up for it let’s first compute the unit vectors from scratch. I’ll use geometric algebra to do this calculation. Consider figure (\ref{fig:qmTwoExamReflection:continuumL2fig5})

\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{continuumL2fig5}
\caption{Composite rotations for spherical polar unit vectors.}
\end{figure}

We have two sets of rotations, the first is a rotation about the z axis by \phi. Writing i = \mathbf{e}_1 \mathbf{e}_2 for the unit bivector in the x,y plane, we rotate

\begin{aligned}\mathbf{e}_1' &= \mathbf{e}_1 e^{i\phi} = \mathbf{e}_1 \cos\phi + \mathbf{e}_2 \sin\phi \\ \mathbf{e}_2' &= \mathbf{e}_2 e^{i\phi} = \mathbf{e}_2 \cos\phi - \mathbf{e}_1 \sin\phi \\ \mathbf{e}_3' &= \mathbf{e}_3\end{aligned} \hspace{\stretch{1}}(3.66)

Now we rotate in the plane spanned by \mathbf{e}_3 and \mathbf{e}_1' by \theta. With j = \mathbf{e}_3 \mathbf{e}_1', our vectors in the plane rotate as

\begin{aligned}\mathbf{e}_1'' &= \mathbf{e}_1' e^{j\phi} = \mathbf{e}_1 e^{i\phi} e^{j\theta} \\ \mathbf{e}_3'' &= \mathbf{e}_3' e^{j\theta} = \mathbf{e}_3 e^{j\theta},\end{aligned} \hspace{\stretch{1}}(3.69)

(with \mathbf{e}_2'' = \mathbf{e}_2 since \mathbf{e}_2 \cdot j = 0).

\begin{aligned}\hat{\boldsymbol{\theta}} = \mathbf{e}_1''&= \mathbf{e}_1 e^{i\phi} e^{j\theta} \\ &= \mathbf{e}_1 e^{i\phi} (\cos\theta + \mathbf{e}_3 \mathbf{e}_1 e^{i\phi} \sin\theta) \\ &= \mathbf{e}_1 e^{i\phi} \cos\theta -\mathbf{e}_3 \sin\theta \\ &= (\mathbf{e}_1 \cos\phi + \mathbf{e}_2 \sin\phi) \cos\theta -\mathbf{e}_3 \sin\theta \\ \end{aligned}

\begin{aligned}\hat{\mathbf{r}} = \mathbf{e}_3''&= \mathbf{e}_3 e^{j\theta} \\ &= \mathbf{e}_3 (\cos\theta + \mathbf{e}_3 \mathbf{e}_1 e^{i\phi} \sin\theta) \\ &= \mathbf{e}_3 \cos\theta + \mathbf{e}_1 e^{i\phi} \sin\theta \\ &= \mathbf{e}_3 \cos\theta + (\mathbf{e}_1 \cos\phi + \mathbf{e}_2 \sin\phi) \sin\theta \\ \end{aligned}

Now, these are all the same relations that we could find with coordinate algebra

\begin{aligned}\hat{\mathbf{r}} &= \mathbf{e}_1 \cos\phi \sin\theta +\mathbf{e}_2 \sin\phi \sin\theta +\mathbf{e}_3 \cos\theta \\ \hat{\boldsymbol{\theta}} &= \mathbf{e}_1 \cos\phi \cos\theta +\mathbf{e}_2 \sin\phi \cos\theta -\mathbf{e}_3 \sin\theta \\ \hat{\boldsymbol{\phi}} &= -\mathbf{e}_1 \sin\phi + \mathbf{e}_2 \cos\phi\end{aligned} \hspace{\stretch{1}}(3.71)

There’s nothing special in this approach if that is as far as we go, but we can put things in a nice tidy form for computation of the differentials of the unit vectors. Introducing the unit pseudoscalar I = \mathbf{e}_1 \mathbf{e}_2 \mathbf{e}_3 we can write these in a compact exponential form.

\begin{aligned}\hat{\mathbf{r}}&= (\mathbf{e}_1 \cos\phi +\mathbf{e}_2 \sin\phi ) \sin\theta +\mathbf{e}_3 \cos\theta \\ &= \mathbf{e}_1 e^{i\phi} \sin\theta +\mathbf{e}_3 \cos\theta \\ &= \mathbf{e}_3 ( \cos\theta + \mathbf{e}_3 \mathbf{e}_1 e^{i\phi} \sin\theta ) \\ &= \mathbf{e}_3 ( \cos\theta + \mathbf{e}_3 \mathbf{e}_1 \mathbf{e}_2 \mathbf{e}_2 e^{i\phi} \sin\theta ) \\ &= \mathbf{e}_3 ( \cos\theta + I \hat{\boldsymbol{\phi}} \sin\theta ) \\ &= \mathbf{e}_3 e^{ I \hat{\boldsymbol{\phi}} \theta }\end{aligned}

\begin{aligned}\hat{\boldsymbol{\theta}}&=\mathbf{e}_1 \cos\phi \cos\theta +\mathbf{e}_2 \sin\phi \cos\theta -\mathbf{e}_3 \sin\theta \\ &=(\mathbf{e}_1 \cos\phi +\mathbf{e}_2 \sin\phi ) \cos\theta -\mathbf{e}_3 \sin\theta \\ &=\mathbf{e}_1 e^{i\phi} \cos\theta -\mathbf{e}_3 \sin\theta \\ &=\mathbf{e}_1 e^{i\phi} ( \cos\theta - e^{-i\phi} \mathbf{e}_1 \mathbf{e}_3 \sin\theta ) \\ &=\mathbf{e}_1 e^{i\phi} ( \cos\theta - \mathbf{e}_1 \mathbf{e}_3 e^{i\phi} \sin\theta ) \\ &=\mathbf{e}_1 e^{i\phi} ( \cos\theta - \mathbf{e}_1 \mathbf{e}_3 \mathbf{e}_2 \mathbf{e}_2 e^{i\phi} \sin\theta ) \\ &=\mathbf{e}_1 e^{i\phi} ( \cos\theta + I \hat{\boldsymbol{\phi}} \sin\theta ) \\ &=\mathbf{e}_1 \mathbf{e}_2 \mathbf{e}_2 e^{i\phi} ( \cos\theta + I \hat{\boldsymbol{\phi}} \sin\theta ) \\ &=i \hat{\boldsymbol{\phi}} e^{I \hat{\boldsymbol{\phi}} \theta}.\end{aligned}

To summarize we have

\begin{aligned}\hat{\boldsymbol{\phi}} &= \mathbf{e}_2 e^{i\phi} \\ \hat{\mathbf{r}} &= \mathbf{e}_3 e^{I\hat{\boldsymbol{\phi}} \theta} \\ \hat{\boldsymbol{\theta}} &= i \hat{\boldsymbol{\phi}} e^{I\hat{\boldsymbol{\phi}} \theta}.\end{aligned} \hspace{\stretch{1}}(3.74)

Taking differentials we find first

\begin{aligned}d\hat{\boldsymbol{\phi}} = \mathbf{e}_2 e^{i\phi} i d\phi = \hat{\boldsymbol{\phi}} i d\phi\end{aligned}

\begin{aligned}d\hat{\boldsymbol{\theta}}&= d \left( i \hat{\boldsymbol{\phi}} e^{I\hat{\boldsymbol{\phi}} \theta} \right) \\ &= i d \hat{\boldsymbol{\phi}} e^{I\hat{\boldsymbol{\phi}} \theta} + i \hat{\boldsymbol{\phi}} d \left( \cos\theta + I \hat{\boldsymbol{\phi}} \sin\theta \right) \\ &= i d \hat{\boldsymbol{\phi}} e^{I\hat{\boldsymbol{\phi}} \theta}+ i \hat{\boldsymbol{\phi}} I (d \hat{\boldsymbol{\phi}}) \sin\theta+ i \hat{\boldsymbol{\phi}} I \hat{\boldsymbol{\phi}} e^{I\hat{\boldsymbol{\phi}} \theta} d\theta \\ &= i \hat{\boldsymbol{\phi}} i e^{I\hat{\boldsymbol{\phi}} \theta} d\phi+ i \hat{\boldsymbol{\phi}} I \hat{\boldsymbol{\phi}} i \sin\theta d\phi+ i \hat{\boldsymbol{\phi}} I \hat{\boldsymbol{\phi}} e^{I\hat{\boldsymbol{\phi}} \theta} d\theta \\ &= \hat{\boldsymbol{\phi}} e^{I\hat{\boldsymbol{\phi}} \theta} d\phi- I \sin\theta d\phi- \mathbf{e}_3 e^{I\hat{\boldsymbol{\phi}} \theta} d\theta \\ &= \hat{\boldsymbol{\phi}} (\cos\theta + I \hat{\boldsymbol{\phi}} \sin\theta) d\phi- I \sin\theta d\phi- \mathbf{e}_3 e^{I\hat{\boldsymbol{\phi}} \theta} d\theta \\ &= \hat{\boldsymbol{\phi}} \cos\theta d\phi - \hat{\mathbf{r}} d\theta\end{aligned}

\begin{aligned}d \hat{\mathbf{r}}&=\mathbf{e}_3 d \left( e^{I\hat{\boldsymbol{\phi}} \theta} \right) \\ &=\mathbf{e}_3 d \left( \cos\theta + I \hat{\boldsymbol{\phi}} \sin\theta \right) \\ &=\mathbf{e}_3 \left( I (d \hat{\boldsymbol{\phi}}) \sin\theta + I \hat{\boldsymbol{\phi}} e^{I\hat{\boldsymbol{\phi}} \theta} d\theta \right) \\ &=\mathbf{e}_3 \left( I \hat{\boldsymbol{\phi}} i \sin\theta d\phi + I \hat{\boldsymbol{\phi}} e^{I\hat{\boldsymbol{\phi}} \theta} d\theta \right) \\ &=i \hat{\boldsymbol{\phi}} i \sin\theta d\phi + i \hat{\boldsymbol{\phi}} e^{I\hat{\boldsymbol{\phi}} \theta} d\theta \\ &=\hat{\boldsymbol{\phi}} \sin\theta d\phi + \hat{\boldsymbol{\theta}} d\theta\end{aligned}

Summarizing these differentials we have

\begin{aligned}d\hat{\mathbf{r}} &= \hat{\boldsymbol{\phi}} \sin\theta d\phi + \hat{\boldsymbol{\theta}} d\theta \\ d\hat{\boldsymbol{\theta}} &= \hat{\boldsymbol{\phi}} \cos\theta d\phi - \hat{\mathbf{r}} d\theta \\ d\hat{\boldsymbol{\phi}} &= \hat{\boldsymbol{\phi}} i d\phi\end{aligned} \hspace{\stretch{1}}(3.77)

A final cleanup is required. While \hat{\boldsymbol{\phi}} i is a vector and has a nicely compact form, we need to decompose this into components in the \hat{\mathbf{r}}, \hat{\boldsymbol{\theta}} and \hat{\boldsymbol{\phi}} directions. Taking scalar products we have

\begin{aligned}\hat{\boldsymbol{\phi}} \cdot (\hat{\boldsymbol{\phi}} i) = 0\end{aligned}

\begin{aligned}\hat{\mathbf{r}} \cdot (\hat{\boldsymbol{\phi}} i)&=\left\langle{{ \hat{\mathbf{r}} \hat{\boldsymbol{\phi}} i}}\right\rangle \\ &=\left\langle{{ \mathbf{e}_3 e^{I\hat{\boldsymbol{\phi}} \theta} \mathbf{e}_2 e^{i\phi} i}}\right\rangle \\ &=\left\langle{{ \mathbf{e}_3 (\cos\theta + I \mathbf{e}_2 e^{i\phi} \sin\theta) \mathbf{e}_2 e^{i\phi} i}}\right\rangle \\ &=\left\langle{{ I (\cos\theta e^{-i\phi} + I \mathbf{e}_2 \sin\theta) \mathbf{e}_2 }}\right\rangle \\ &=-\sin\theta\end{aligned}

\begin{aligned}\hat{\boldsymbol{\theta}} \cdot (\hat{\boldsymbol{\phi}} i)&=\left\langle{{ \hat{\boldsymbol{\theta}} \hat{\boldsymbol{\phi}} i }}\right\rangle \\ &=\left\langle{{ i \hat{\boldsymbol{\phi}} e^{I\hat{\boldsymbol{\phi}} \theta} \hat{\boldsymbol{\phi}} i }}\right\rangle \\ &=-\left\langle{{ \hat{\boldsymbol{\phi}} e^{I\hat{\boldsymbol{\phi}} \theta} \hat{\boldsymbol{\phi}} }}\right\rangle \\ &=-\left\langle{{ e^{I\hat{\boldsymbol{\phi}} \theta} }}\right\rangle \\ &=- \cos\theta.\end{aligned}

Summarizing once again, but this time in terms of \hat{\mathbf{r}}, \hat{\boldsymbol{\theta}} and \hat{\boldsymbol{\phi}} we have

\begin{aligned}d\hat{\mathbf{r}} &= \hat{\boldsymbol{\phi}} \sin\theta d\phi + \hat{\boldsymbol{\theta}} d\theta \\ d\hat{\boldsymbol{\theta}} &= \hat{\boldsymbol{\phi}} \cos\theta d\phi - \hat{\mathbf{r}} d\theta \\ d\hat{\boldsymbol{\phi}} &= -(\hat{\mathbf{r}} \sin\theta + \hat{\boldsymbol{\theta}} \cos\theta) d\phi\end{aligned} \hspace{\stretch{1}}(3.80)

Now we are set to take differentials. With

\begin{aligned}\mathbf{x} = r \hat{\mathbf{r}},\end{aligned} \hspace{\stretch{1}}(3.83)

we have

\begin{aligned}d\mathbf{x} =dr \hat{\mathbf{r}}+ r d\hat{\mathbf{r}}=dr \hat{\mathbf{r}} + \hat{\boldsymbol{\phi}} r \sin\theta d\phi + r \hat{\boldsymbol{\theta}} d\theta.\end{aligned} \hspace{\stretch{1}}(3.84)

Squaring this we get the usual spherical polar line scalar line element

\begin{aligned}d\mathbf{x}^2 = dr^2 + r^2 \sin^2\theta d\phi^2 + r^2 d\theta^2.\end{aligned} \hspace{\stretch{1}}(3.85)

With

\begin{aligned}\mathbf{u} = u_r \hat{\mathbf{r}} + u_\theta \hat{\boldsymbol{\theta}} + u_\phi \hat{\boldsymbol{\phi}},\end{aligned} \hspace{\stretch{1}}(3.86)

our differential is

\begin{aligned}d\mathbf{u}&=du_r \hat{\mathbf{r}} + du_\theta \hat{\boldsymbol{\theta}} + du_\phi \hat{\boldsymbol{\phi}}+ u_r d\hat{\mathbf{r}} + u_\theta d\hat{\boldsymbol{\theta}} + u_\phi d \hat{\boldsymbol{\phi}} \\ &=du_r \hat{\mathbf{r}} + du_\theta \hat{\boldsymbol{\theta}} + du_\phi \hat{\boldsymbol{\phi}}+ u_r \left(\hat{\boldsymbol{\phi}} \sin\theta d\phi + \hat{\boldsymbol{\theta}} d\theta \right)+ u_\theta \left( \hat{\boldsymbol{\phi}} \cos\theta d\phi - \hat{\mathbf{r}} d\theta \right)- u_\phi (\hat{\mathbf{r}} \sin\theta + \hat{\boldsymbol{\theta}} \cos\theta) d\phi\\ &=\hat{\mathbf{r}} \left( du_r - u_\theta d\theta - u_\phi \sin\theta d\phi \right) \\ &+\hat{\boldsymbol{\theta}} \left( du_\theta + u_r d\theta - u_\phi \cos\theta d\phi \right) \\ &+\hat{\boldsymbol{\phi}} \left( du_\phi + u_r \sin\theta d\phi + u_\theta \cos\theta d\phi \right).\end{aligned}

We can add d\mathbf{x} to this and take differences

\begin{aligned}\begin{aligned}(d\mathbf{u} + d\mathbf{x})^2 - d\mathbf{x}^2&=\left( du_r - u_\theta d\theta - u_\phi \sin\theta d\phi + dr \right)^2 \\ &+\left( du_\theta + u_r d\theta - u_\phi \cos\theta d\phi + r d\theta \right)^2 \\ &+\left( du_\phi + u_r \sin\theta d\phi + u_\theta \cos\theta d\phi + r \sin\theta d\phi \right)^2\end{aligned}\end{aligned} \hspace{\stretch{1}}(3.87)

For each m = r,\theta,\phi we have

\begin{aligned}du_m=\frac{\partial {u_m}}{\partial {r}} dr +\frac{\partial {u_m}}{\partial {\theta}} d\theta +\frac{\partial {u_m}}{\partial {\phi}} d\phi,\end{aligned} \hspace{\stretch{1}}(3.88)

and plugging through that calculation is really all it takes to derive the textbook result. To do this to first order in u_m, we find

\begin{aligned}\frac{1}{{2}} \left((d\mathbf{u} + d\mathbf{x})^2 - d\mathbf{x}^2\right)&=du_r dr- u_\theta d\theta dr- u_\phi \sin\theta d\phi dr \\ &+ du_\theta r d\theta+ u_r r d\theta^2- u_\phi r \cos\theta d\phi d\theta \\ &+ r \sin\theta du_\phi d\phi+ r \sin^2\theta u_r d\phi^2+ r \sin\theta \cos\theta u_\theta d\phi^2 \\ &=\left( \frac{\partial {u_r}}{\partial {r}} dr + \frac{\partial {u_r}}{\partial {\theta}} d\theta + \frac{\partial {u_r}}{\partial {\phi}} d\phi \right)dr- u_\theta d\theta dr- u_\phi \sin\theta d\phi dr \\ &+\left( \frac{\partial {u_\theta}}{\partial {r}} dr + \frac{\partial {u_\theta}}{\partial {\theta}} d\theta + \frac{\partial {u_\theta}}{\partial {\phi}} d\phi \right) r d\theta+ u_r r d\theta^2- u_\phi r \cos\theta d\phi d\theta \\ &+\left( \frac{\partial {u_\phi}}{\partial {r}} dr + \frac{\partial {u_\phi}}{\partial {\theta}} d\theta + \frac{\partial {u_\phi}}{\partial {\phi}} d\phi \right)r \sin\theta d\phi+ r \sin^2\theta u_r d\phi^2+ r \sin\theta \cos\theta u_\theta d\phi^2\end{aligned}

Collecting terms we have the result of the text in the braces

\begin{aligned}\begin{aligned}\left((d\mathbf{u} + d\mathbf{x})^2 - d\mathbf{x}^2\right)&=2 dr^2 \left(\frac{\partial {u_r}}{\partial {r}}\right) \\ &+2 r^2 d\theta^2 \left(\frac{1}{{r}} \frac{\partial {u_\theta}}{\partial {\theta}} + u_r \frac{1}{{r}}\right) \\ &+2 r^2 \sin^2\theta d\phi^2 \left(\frac{\partial {u_\phi}}{\partial {\phi}} \frac{1}{{r \sin\theta}} + \frac{1}{{r}} u_r + \frac{1}{{r}} \cot\theta u_\theta\right) \\ &+2 dr r d\theta \left(\frac{1}{{r}} \frac{\partial {u_r}}{\partial {\theta}} - \frac{1}{{r}} u_\theta +\frac{\partial {u_\theta}}{\partial {r}}\right) \\ &+2 r^2 \sin\theta d\theta d\phi \left(\frac{\partial {u_\theta}}{\partial {\phi}} \frac{1}{{r \sin\theta}} - \frac{1}{{r}} u_\phi \cot\theta +\frac{1}{{r}} \frac{\partial {u_\phi}}{\partial {\theta}}\right) \\ &+2 r \sin\theta d\phi dr \left(\frac{1}{{r \sin\theta}} \frac{\partial {u_r}}{\partial {\phi}} - \frac{1}{{r}} u_\phi + \frac{\partial {u_\phi}}{\partial {r}}\right)\end{aligned}\end{aligned} \hspace{\stretch{1}}(3.89)

It should be possible to do the calculation to second order too, but to include all the quadratic terms in u_m is again really messy. Trying that with mathematica gives the same results as above using the strictly coordinate algebra approach.

References

[1] L.D. Landau, EM Lifshitz, JB Sykes, WH Reid, and E.H. Dill. Theory of elasticity: Vol. 7 of course of theoretical physics. 1960.

Posted in Math and Physics Learning. | Tagged: , , , , , , , , | Leave a Comment »

PHY454H1S Continuum Mechanics. Lecture 4: Strain tensor components. Taught by Prof. K. Das.

Posted by peeterjoot on January 21, 2012

[Click here for a PDF of this post with nicer formatting and figures if the post had any (especially if my latex to wordpress script has left FORMULA DOES NOT PARSE errors.)]

Disclaimer.

Peeter’s lecture notes from class. May not be entirely coherent.

Stress tensor.

Reading: Portions of this lecture cover section 2 from the text [1].

For the stress tensor

\begin{aligned}\sigma_{ij},\end{aligned} \hspace{\stretch{1}}(2.1)

a second rank tensor, the first index i defines the direction of the force, and the second index j defines the surface.

Observe that the dimensions of \sigma_{ij} is force per unit area, just like pressure. We will in fact show that this tensor is akin to the pressure, and the diagonalized components of this tensor represent the pressure.

We’ve illustrated the stress tensor in a couple of 2D examples. The first we call uniaxial stress, having just the 1,1 element of the matrix as illustrated in figure (\ref{fig:continuumL4:continuumL4fig1})

\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{continuumL4fig1}
\caption{Uniaxial stress}
\end{figure}

\begin{aligned}\sigma = \begin{bmatrix}\sigma_{11} & 0 \\ 0 & 0\end{bmatrix}.\end{aligned} \hspace{\stretch{1}}(2.2)

A biaxial stress is illustrated in figure (\ref{fig:continuumL4:continuumL4fig2})
\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{continuumL4fig2}
\caption{Biaxial stress.}
\end{figure}

where for \sigma_{11} \ne \sigma_{22} our tensor takes the form

\begin{aligned}\sigma = \begin{bmatrix}\sigma_{11} & 0 \\ 0 & \sigma_{22}\end{bmatrix}.\end{aligned} \hspace{\stretch{1}}(2.3)

In the general case we have

\begin{aligned}\sigma = \begin{bmatrix}\sigma_{11} & \sigma_{12} \\ \sigma_{21} & \sigma_{22}\end{bmatrix}.\end{aligned} \hspace{\stretch{1}}(2.4)

We can attempt to illustrate this, but it becomes much harder to visualize as shown in figure (\ref{fig:continuumL4:continuumL4fig3})
\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{continuumL4fig3}
\caption{General strain}
\end{figure}

In equilibrium we must have

\begin{aligned}\sigma_{12} = \sigma_{21}.\end{aligned} \hspace{\stretch{1}}(2.5)

We can use similar arguments to show that the stress tensor is symmetric.

In 3D we have three components of the stress tensor acting on each surface, as illustrated in figure (\ref{fig:continuumL4:continuumL4fig5})
\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{continuumL4fig5}
\caption{Strain components on a 3D volume.}
\end{figure}

We have three unique surface orientations and three components of the force for each of these, resulting in nine components, but these are not all independent. For an object in equilibrium we must have \sigma_{ij} = \sigma_{ji} (FIXME: justify?). Explicitly, that is

\begin{aligned}\sigma_{12} &= \sigma_{21} \\ \sigma_{23} &= \sigma_{32} \\ \sigma_{31} &= \sigma_{13}\end{aligned} \hspace{\stretch{1}}(2.6)

Diagonalization

We’ll look at the two dimensional case in some detail, as in figure (\ref{fig:continuumL4:continuumL4fig6})

\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{continuumL4fig6}
\caption{Area element under strain with and without rotation.}
\end{figure}

Under this coordinate transformation, a rotation, the diagonal stress tensor is taken to a non-diagonal form

\begin{aligned}\begin{bmatrix}\sigma_{11} & 0 \\ 0 & \sigma_{22} \end{bmatrix}\leftrightarrow\begin{bmatrix}\sigma_{11}' & \sigma_{12}' \\ \sigma_{21}' & \sigma_{22}' \end{bmatrix}\end{aligned} \hspace{\stretch{1}}(2.9)

How do the stress tensor and the force relate

We form a Cauchy tetrahedron as in figure (\ref{fig:continuumL4:continuumL4fig7})
\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{continuumL4fig7}
\caption{Cauchy tetrahedron}
\end{figure}

\begin{aligned}\mathbf{f} = \frac{\text{external force}}{\text{unit area}} = f_j \mathbf{e}_j\end{aligned} \hspace{\stretch{1}}(2.10)

\begin{aligned}\text{internal stress} = \text{external force}\end{aligned} \hspace{\stretch{1}}(2.11)

We write \hat{\mathbf{n}} in terms of the direction cosines

\begin{aligned}\hat{\mathbf{n}} = n_1 \mathbf{e}_1 + n_2 \mathbf{e}_2 + n_3 \mathbf{e}_3 \end{aligned} \hspace{\stretch{1}}(2.12)

Here

\begin{aligned}n_1 &= \hat{\mathbf{n}} \cdot \mathbf{e}_1 \\ n_2 &= \hat{\mathbf{n}} \cdot \mathbf{e}_2 \\ n_3 &= \hat{\mathbf{n}} \cdot \mathbf{e}_3,\end{aligned} \hspace{\stretch{1}}(2.13)

or

\begin{aligned}n_j = \hat{\mathbf{n}} \cdot \mathbf{e}_j = \cos\phi_j\end{aligned} \hspace{\stretch{1}}(2.16)

Force balance on x_1 direction, matching total external force in this direction to the total internal force (\sigma_{ij}'s) as follows

\begin{aligned}\begin{aligned}f_1 \times \text{area ABC} &= \sigma_{11} \times \text{area BOC} \\ &+\sigma_{12} \times \text{area AOC} \\ &+\sigma_{13} \times \text{area AOB}\end{aligned}\end{aligned} \hspace{\stretch{1}}(2.17)

Similarily

\begin{aligned}\begin{aligned}f_2 \times \text{area ABC} &= \sigma_{21} \times \text{area BOC} \\ &+\sigma_{22} \times \text{area AOC} \\ &+\sigma_{23} \times \text{area AOB},\end{aligned}\end{aligned} \hspace{\stretch{1}}(2.18)

and

\begin{aligned}\begin{aligned}f_3 \times \text{area ABC} &= \sigma_{31} \times \text{area BOC} \\ &+\sigma_{32} \times \text{area AOC} \\ &+\sigma_{33} \times \text{area AOB},\end{aligned}\end{aligned} \hspace{\stretch{1}}(2.19)

We can therefore write these force components like

\begin{aligned}f_1 = \sigma_{11} \frac{BOC}{ABC} + \sigma_{12} \frac{AOC}{ABC} + \sigma_{13} \frac{AOB}{ABC} \end{aligned} \hspace{\stretch{1}}(2.20)

but these ratios are really just the projections of the areas as illustrated in figure (\ref{fig:continuumL4:continuumL4fig8})

\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{continuumL4fig8}
\caption{Area projection.}
\end{figure}

where an arbitrary surface with area \Delta S can be decomposed into projections

\begin{aligned}\Delta S \cos\phi_j,\end{aligned} \hspace{\stretch{1}}(2.21)

utilizing the direction cosines. We can therefore write

\begin{aligned}f_1 &= \sigma_{11} n_1 + \sigma_{12} n_2 + \sigma_{13} n_3 \\ f_2 &= \sigma_{21} n_1 + \sigma_{22} n_2 + \sigma_{23} n_3 \\ f_3 &= \sigma_{31} n_1 + \sigma_{32} n_2 + \sigma_{33} n_3,\end{aligned} \hspace{\stretch{1}}(2.22)

or in matrix notation

\begin{aligned}\begin{bmatrix}f_1 \\ f_2 \\ f_3 \end{bmatrix}=\begin{bmatrix}\sigma_{11} & \sigma_{12} & \sigma_{13} \\ \sigma_{21} & \sigma_{22} & \sigma_{23} \\ \sigma_{31} & \sigma_{32} & \sigma_{33} \end{bmatrix}\begin{bmatrix}n_1 \\ n_2 \\ n_3 \\ \end{bmatrix}.\end{aligned} \hspace{\stretch{1}}(2.25)

This is just

\begin{aligned}\boxed{f_i = \sigma_{ij} n_j.}\end{aligned} \hspace{\stretch{1}}(2.26)

This force with components f_i is also called the traction vector

\begin{aligned}T_i = \sigma_{ij} n_j.\end{aligned} \hspace{\stretch{1}}(2.27)

References

[1] L.D. Landau, EM Lifshitz, JB Sykes, WH Reid, and E.H. Dill. Theory of elasticity: Vol. 7 of course of theoretical physics. Physics Today, 13:44, 1960.

Posted in Math and Physics Learning. | Tagged: , , , , , | Leave a Comment »

PHY454H1S Continuum Mechanics. Lecture 2. Introduction and strain tensor. Taught by Prof. K. Das.

Posted by peeterjoot on January 21, 2012

[Click here for a PDF of this post with nicer formatting and figures if the post had any (especially if my latex to wordpress script has left FORMULA DOES NOT PARSE errors.)]

Disclaimer.

Peeter’s lecture notes from class. May not be entirely coherent.

Introduction.

Mechanics could be defined as the study of effects of forces and displacements on a physical body

\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{continuumL2fig1}
\caption{Physical body.}
\end{figure}

In continuum mechanics we have a physical body and we are interested in the internal motions in the object.

\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{continuumL2fig2}
\caption{Control volume elements.}
\end{figure}

For the first time considering mechanics we have to introduce the concepts of fields to make progress tackling these problems.

We will have use of the following types of fields

\begin{itemize}
\item Scalar fields. 3^0 components. Examples: density, Temperature, …
\item Vector fields. 3^1 components. Examples: Force, velocity.
\item Tensor fields. 3^2 components. Examples: stress, strain.
\end{itemize}

We have to consider objects (a control volume) that is small enough that we can consider that we have a point in space limit for the quantities of density and velocity. At the same time we cannot take this limiting process to the extreme, since if we use a control volume that is sufficiently small, quantum and inter-atomic effects would have to be considered.

\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{continuumL2fig3}
\caption{Mass and volume ratios at different scales.}
\end{figure}

Stress and Strain definitions.

\begin{definition}
\emph{(Stress)}

Measure of the Internal force on the surfaces.
\end{definition}

\begin{definition}
\emph{(Strain)}

Measure of the deformation of the body.
\end{definition}

Strain Tensor.

This follows [1] section 1 very closely.

Utilizing summation convention consider a set of small internal displacements u_1, u_2, u_3 to the x, y, z coordinates so that the transformation x_i \rightarrow x_i' is related by

\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{continuumL2fig4}
\caption{Differential change to the object.}
\end{figure}

\begin{aligned}u_i &= x_i' - x_i \\ x_i' &= g(x_i) \\ u_i &= f(x_i)\end{aligned} \hspace{\stretch{1}}(3.1)

(ie: x_i' is a function of all the initial coordinates, as are the displacements u_i).

\begin{aligned}dx_i' = dx_i + du_i\end{aligned} \hspace{\stretch{1}}(3.4)

\begin{aligned}dl &= \sqrt{dx_k dx_k} \\ dl' &= \sqrt{d{x'}_k d{x'}_k}\end{aligned} \hspace{\stretch{1}}(3.5)

or

\begin{aligned}{dl'}^2 = (dx_k + du_k)(dx_k + du_k)= dl^2 + 2 dx_k du_k + du_k du_k\end{aligned} \hspace{\stretch{1}}(3.7)

with

\begin{aligned}du_i = \frac{\partial {u_i}}{\partial {x_k}} dx_k\end{aligned} \hspace{\stretch{1}}(3.8)

we have

\begin{aligned}du_i^2 = \frac{\partial {u_i}}{\partial {x_k}} dx_k\frac{\partial {u_i}}{\partial {x_l}} dx_l\end{aligned} \hspace{\stretch{1}}(3.9)

\begin{aligned}{dl'}^2 &= dl^2 + 2 \frac{\partial {u_i}}{\partial {x_k}} dx_k dx_i + \frac{\partial {u_l}}{\partial {x_i}} \frac{\partial {u_l}}{\partial {x_k}} dx_i dx_k \\ &= dl^2 + \left(\frac{\partial {u_i}}{\partial {x_k}} +\frac{\partial {u_k}}{\partial {x_i}} \right)dx_k dx_i + \frac{\partial {u_l}}{\partial {x_i}} \frac{\partial {u_l}}{\partial {x_k}} dx_i dx_k \\ &=dl^2 + 2 e_{ik} dx_i dx_k\end{aligned}

We write

\begin{aligned}{dl'}^2 - dl^2 = 2 e_{ik} dx_i dx_k\end{aligned} \hspace{\stretch{1}}(3.10)

where we define the \emph{strain tensor} as

\begin{aligned}e_{ik} = \frac{1}{{2}} \left(\left(\frac{\partial {u_i}}{\partial {x_k}} +\frac{\partial {u_k}}{\partial {x_i}} \right)+ \frac{\partial {u_l}}{\partial {x_i}} \frac{\partial {u_l}}{\partial {x_k}} \right)\end{aligned} \hspace{\stretch{1}}(3.11)

Here e_{ik} is a 3 \times 3 matrix in Cartesian coordinates

\begin{aligned}\begin{bmatrix}e_{11} & e_{12} & e_{13} \\ e_{21} & e_{22} & e_{23} \\ e_{31} & e_{32} & e_{33} \\ \end{bmatrix}\end{aligned} \hspace{\stretch{1}}(3.12)

We see from 3.11 that e_{ik} is symmetric, so we have

\begin{aligned}e_{21} &= e_{12} \\ e_{31} &= e_{13} \\ e_{32} &= e_{23}\end{aligned} \hspace{\stretch{1}}(3.13)

Because any real symmetric matrix can be diagonalized we can write in some coordinate system

\begin{aligned}\bar{e}_{ik} = \begin{bmatrix}\bar{e}_{11} & 0 & 0 \\ 0 & \bar{e}_{22} & 0 \\ 0 & 0 & \bar{e}_{33} \\ \end{bmatrix}\end{aligned} \hspace{\stretch{1}}(3.16)

\begin{aligned}{dx_1'}^2 &= (1 + 2 \bar{e}_{11}) dx_1^2 \\ {dx_2'}^2 &= (1 + 2 \bar{e}_{22}) dx_2^2 \\ {dx_3'}^2 &= (1 + 2 \bar{e}_{33}) dx_3^2\end{aligned} \hspace{\stretch{1}}(3.17)

If our changes are small enough we can also write approximately, taking the first order term in the square root evaluation

\begin{aligned}dx_1' &\approx (1 + \bar{e}_{11}) dx_1 \\ dx_2' &\approx (1 + \bar{e}_{22}) dx_2 \\ dx_3' &\approx (1 + \bar{e}_{33}) dx_3\end{aligned} \hspace{\stretch{1}}(3.20)

We are also free to define a volume element

\begin{aligned}dV' = dx_1'dx_2'dx_3'\approx(1 + e_{11})(1 + e_{22})(1 + e_{33})dx_1 dx_2 dx_3\end{aligned} \hspace{\stretch{1}}(3.23)

\begin{aligned}dV' = (1 + e_{11} +e_{22} +e_{33} ) dV\end{aligned} \hspace{\stretch{1}}(3.24)

So the change of volume is given by the trace

\begin{aligned}dV' = ( 1 + e_{ii} )^2 dV\end{aligned} \hspace{\stretch{1}}(3.25)

Strain Tensor in cylindrical coordinates.

At the end of the section in the text, the formulas for the spherical and cylindrical versions (to first order) of the strain tensor is given without derivation. Let’s do that derivation for the cylindrical case, which is simpler. It appears that use of explicit vector notation is helpful here, so we write

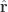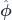\begin{aligned}\mathbf{x} &= r \hat{\mathbf{r}} + z \hat{\mathbf{z}} \\ \mathbf{u} & u_r \hat{\mathbf{r}} + u_\phi \hat{\boldsymbol{\phi}} + u_z \hat{\mathbf{z}}\end{aligned} \hspace{\stretch{1}}(3.26)

where

\begin{aligned}\hat{\mathbf{r}} &= \mathbf{e}_1 e^{i\phi} \\ \hat{\boldsymbol{\phi}} &= \mathbf{e}_2 e^{i\phi} \\ i &= \mathbf{e}_1 \mathbf{e}_2\end{aligned} \hspace{\stretch{1}}(3.28)

Since \hat{\mathbf{r}} and \hat{\boldsymbol{\phi}} are functions of position, we will need their differentials

\begin{aligned}d\hat{\mathbf{r}} &= \mathbf{e}_1 \mathbf{e}_1 \mathbf{e}_2 e^{i\phi} d\phi = \mathbf{e}_2 e^{i \phi} d\phi \\ d\hat{\boldsymbol{\phi}} &= \mathbf{e}_2 \mathbf{e}_1 \mathbf{e}_2 e^{i\phi} d\phi = -\mathbf{e}_2 e^{i \phi} d\phi,\end{aligned} \hspace{\stretch{1}}(3.31)

but these are just scaled basis vectors

\begin{aligned}d\hat{\mathbf{r}} &= \hat{\boldsymbol{\phi}} d\phi \\ d\hat{\boldsymbol{\phi}} &= -\hat{\mathbf{r}} d\phi.\end{aligned} \hspace{\stretch{1}}(3.33)

So for our 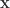\mathbf{x} and \mathbf{u} differentials we find

\begin{aligned}d\mathbf{x} &= dr \hat{\mathbf{r}} + r d\hat{\mathbf{r}} + dz \hat{\mathbf{z}} \\ &= dr \hat{\mathbf{r}} + r \hat{\boldsymbol{\phi}} d\phi + dz \hat{\mathbf{z}},\end{aligned}

and

\begin{aligned}d\mathbf{u} &= du_r \hat{\mathbf{r}} + du_\phi \hat{\boldsymbol{\phi}} + du_z \hat{\mathbf{z}} + u_r \hat{\boldsymbol{\phi}} d\phi - u_\phi \hat{\mathbf{r}} d\phi \\ &= \hat{\mathbf{r}}( du_r - u_\phi d\phi )+ \hat{\boldsymbol{\phi}} ( du_\phi + u_r d\phi )+ \hat{\mathbf{z}} ( du_z ).\end{aligned}

Putting these together we have

\begin{aligned}d\mathbf{l}' &= d\mathbf{u} + d\mathbf{x} \\ &= \hat{\mathbf{r}}( du_r - u_\phi d\phi + dr )+ \hat{\boldsymbol{\phi}} ( du_\phi + u_r d\phi + r d\phi )+ \hat{\mathbf{z}} ( du_z + dz ).\end{aligned}

For the squared magnitude’s difference from d\mathbf{x}^2 we have

\begin{aligned}(d\mathbf{l}')^2 - d\mathbf{x}^2&= ( du_r - u_\phi d\phi + dr )^2+ ( du_\phi + u_r d\phi + r d\phi )^2+ ( du_z + dz )^2-dr^2 - r^2 d\phi^2 - dz^2 \\ &=( du_r - u_\phi d\phi )^2 + 2 dr ( du_r - u_\phi d\phi )+ ( du_\phi + u_r d\phi )^2+ 2 r d\phi ( du_\phi + u_r d\phi )+ du_z^2 + 2 du_z dz \\ \end{aligned}

Expanding this out, but dropping all the terms that are quadratic in the components of \mathbf{u} or its differentials, we have

\begin{aligned}(d\mathbf{l}')^2 - d\mathbf{x}^2&\approx 2 dr ( du_r - u_\phi d\phi )+ 2 r d\phi ( du_\phi + u_r d\phi )+ 2 du_z dz \\ &= 2 dr du_r - 2 dr u_\phi d\phi + 2 r d\phi du_\phi + 2 r d\phi u_r d\phi + 2 du_z dz \\ &= 2 dr \left( \frac{\partial {u_r}}{\partial {r}} dr+\frac{\partial {u_r}}{\partial {\phi}} d\phi+\frac{\partial {u_r}}{\partial {z}} dz\right) \\ &- 2 dr d\phi u_\phi \\ &+ 2 r d\phi \left( \frac{\partial {u_\phi}}{\partial {r}} dr+\frac{\partial {u_\phi}}{\partial {\phi}} d\phi+\frac{\partial {u_\phi}}{\partial {z}} dz\right) \\ &+ 2 r d\phi d\phi u_r \\ &+ 2 dz \left( \frac{\partial {u_z}}{\partial {r}} dr+\frac{\partial {u_z}}{\partial {\phi}} d\phi+\frac{\partial {u_z}}{\partial {z}} dz\right) \\ \end{aligned}

Grouping all terms, with all the second order terms neglected, we have

\begin{aligned}\begin{aligned}(d\mathbf{l}')^2 - d\mathbf{x}^2&=2 dr dr \frac{\partial {u_r}}{\partial {r}} + 2 r^2 d\phi d\phi \left( \frac{1}{{r}} \frac{\partial {u_\phi}}{\partial {\phi}} +\frac{1}{{r}} u_r \right)+ 2 dz dz \frac{\partial {u_z}}{\partial {z}} \\ &+ 2 dz dr \left( \frac{\partial {u_r}}{\partial {z}} + \frac{\partial {u_z}}{\partial {r}} \right)+ 2 dr r d\phi \left( \frac{\partial {u_\phi}}{\partial {r}} - \frac{1}{{r}} u_\phi + \frac{1}{{r}} \frac{\partial {u_r}}{\partial {\phi}} \right)+ 2 dz r d\phi \left( \frac{\partial {u_\phi}}{\partial {z}} +\frac{1}{{r}} \frac{\partial {u_z}}{\partial {\phi}} \right).\end{aligned}\end{aligned} \hspace{\stretch{1}}(3.35)

From this we can read off the result quoted in the text

\begin{aligned}2 e_{rr} &= \frac{\partial {u_r}}{\partial {r}} \\ 2 e_{\phi\phi} &= \frac{1}{{r}} \frac{\partial {u_\phi}}{\partial {\phi}} +\frac{1}{{r}} u_r \\ 2 e_{zz} &= \frac{\partial {u_z}}{\partial {z}} \\ 2 e_{zr} &= \frac{\partial {u_r}}{\partial {z}} + \frac{\partial {u_z}}{\partial {r}} \\ 2 e_{r\phi} &= \frac{\partial {u_\phi}}{\partial {r}} - \frac{1}{{r}} u_\phi + \frac{1}{{r}} \frac{\partial {u_r}}{\partial {\phi}} \\ 2 e_{\phi z} &= \frac{\partial {u_\phi}}{\partial {z}} +\frac{1}{{r}} \frac{\partial {u_z}}{\partial {\phi}}.\end{aligned} \hspace{\stretch{1}}(3.36)

Observe that we have to introduce factors of r along with all the d\phi‘s, when we factored out the tensor components. That’s an important looking detail, which isn’t obvious unless one works through the derivation.

Note that in class we retained the second order terms. That becomes a messier calculation and I’ve cheated using the symbolic capabilities of mathematica to do it

\begin{aligned}\begin{aligned}&(d\mathbf{l}')^2 - d\mathbf{x}^2 \\ &= (dr)^2 \left(2 \frac{\partial u_r}{\partial r}+\left(\frac{\partial u_r}{\partial r}\right)^2+\left(\frac{\partial u_z}{\partial r}\right)^2+\left(\frac{\partial u_{\phi }}{\partial r}\right)^2\right) \\ &+(d\phi )^2 \left(2 r u_r+u_r^2+u_{\phi }^2-2 u_{\phi } \frac{\partial u_r}{\partial \phi }+\left(\frac{\partial u_r}{\partial \phi }\right)^2+\left(\frac{\partial u_z}{\partial \phi }\right)^2+2 r \frac{\partial u_{\phi }}{\partial \phi }+2 u_r \frac{\partial u_{\phi }}{\partial \phi }+\left(\frac{\partial u_{\phi }}{\partial \phi }\right)^2\right) \\ &+(dz)^2 \left(\left(\frac{\partial u_r}{\partial z}\right)^2+2 \frac{\partial u_z}{\partial z}+\left(\frac{\partial u_z}{\partial z}\right)^2+\left(\frac{\partial u_{\phi }}{\partial z}\right)^2\right) \\ &+dr d\phi \left(-2 u_{\phi }-2 u_{\phi } \frac{\partial u_r}{\partial r}+2 \frac{\partial u_r}{\partial \phi }+2 \frac{\partial u_r}{\partial r} \frac{\partial u_r}{\partial \phi }+2 \frac{\partial u_z}{\partial r} \frac{\partial u_z}{\partial \phi }+2 r \frac{\partial u_{\phi }}{\partial r}+2 u_r \frac{\partial u_{\phi }}{\partial r}+2 \frac{\partial u_{\phi }}{\partial r} \frac{\partial u_{\phi }}{\partial \phi }\right) \\ &+dz d\phi \left(-2 u_{\phi } \frac{\partial u_r}{\partial z}+2 \frac{\partial u_r}{\partial z} \frac{\partial u_r}{\partial \phi }+2 \frac{\partial u_z}{\partial \phi }+2 \frac{\partial u_z}{\partial z} \frac{\partial u_z}{\partial \phi }+2 r \frac{\partial u_{\phi }}{\partial z}+2 u_r \frac{\partial u_{\phi }}{\partial z}+2 \frac{\partial u_{\phi }}{\partial z} \frac{\partial u_{\phi }}{\partial \phi }\right) \\ &+dr dz \left(2 \frac{\partial u_r}{\partial z}+2 \frac{\partial u_r}{\partial r} \frac{\partial u_r}{\partial z}+2 \frac{\partial u_z}{\partial r}+2 \frac{\partial u_z}{\partial r} \frac{\partial u_z}{\partial z}+2 \frac{\partial u_{\phi }}{\partial r} \frac{\partial u_{\phi }}{\partial z}\right).\end{aligned}\end{aligned} \hspace{\stretch{1}}(3.42)

As with the first order case, we can read off the tensor coordinates by inspection (once we factor out the various factors of 2 and r). The next logical step would be to do the spherical tensor calculation. That would likely be particularily messy if we attempted it in the brute force fashion. Let’s step back and look at the general case, before tackling there sphereical polar form explicitly.

Strain Tensor for general coordinate representation.

Now let’s dispense with the assumption that we have an orthonormal frame. Given an arbitrary, not neccessarily orthonormal, position dependent frame \{e_\mu\}, and its reciprocal frame \{e^\mu\}, as defined by

\begin{aligned}e_\mu \cdot e^\nu = {\delta_\mu}^\nu.\end{aligned} \hspace{\stretch{1}}(3.43)

Our coordinate representation, with summation and dimensionality implied, is

\begin{aligned}\mathbf{x} &= x^\mu e_\mu = x_\nu e^\nu \\ \mathbf{u} &= u^\mu e_\mu = u_\nu e^\nu.\end{aligned} \hspace{\stretch{1}}(3.44)

Our differentials are

\begin{aligned}\begin{aligned}d\mathbf{x} &= dx^\mu e_\mu + x^\mu d e_\mu \\ &= \sum_\alpha d\alpha \left( \frac{\partial {x^\mu}}{\partial {\alpha}} e_\mu+x^\mu\frac{\partial {e_\mu}}{\partial {\alpha}} \right),\end{aligned}\end{aligned} \hspace{\stretch{1}}(3.46)

and

\begin{aligned}\begin{aligned}d\mathbf{u} &= du^\mu e_\mu + u^\mu d e_\mu \\ &= \sum_\alpha d\alpha \left( \frac{\partial {u^\mu}}{\partial {\alpha}} e_\mu+u^\mu\frac{\partial {e_\mu}}{\partial {\alpha}} \right).\end{aligned}\end{aligned} \hspace{\stretch{1}}(3.47)

Summing these we have

\begin{aligned}d\mathbf{u} + d\mathbf{u} = \sum_\alpha d\alpha \left( \left(\frac{\partial {x^\mu}}{\partial {\alpha}} +\frac{\partial {u^\mu}}{\partial {\alpha}} \right)e_\mu+\left(x^\mu+u^\mu\right)\frac{\partial {e_\mu}}{\partial {\alpha}} \right).\end{aligned} \hspace{\stretch{1}}(3.48)

Taking dot products to form the squares we have

\begin{aligned}d\mathbf{x}^2 &= \sum_{\alpha, \beta} d\alpha d\beta \left( \frac{\partial {x^\mu}}{\partial {\alpha}} e_\mu+x^\mu\frac{\partial {e_\mu}}{\partial {\alpha}} \right)\cdot\left( \frac{\partial {x_\nu}}{\partial {\beta}} e^\nu+x_\nu\frac{\partial {e^\nu}}{\partial {\beta}} \right) \\ &=\sum_{\alpha, \beta} d\alpha d\beta \left( \frac{\partial {x^\mu}}{\partial {\alpha}} \frac{\partial {x_\mu}}{\partial {\beta}} +x^\mu x_\nu\frac{\partial {e_\mu}}{\partial {\alpha}} \cdot\frac{\partial {e^\nu}}{\partial {\beta}} + 2 \frac{\partial {x^\mu}}{\partial {\alpha}} x_\nu e_\mu \cdot\frac{\partial {e^\nu}}{\partial {\beta}} \right),\end{aligned}

and

\begin{aligned}&(d\mathbf{u} + d\mathbf{x})^2 \\ &= \sum_{\alpha, \beta}d\alpha d\beta \left( \left(\frac{\partial {x^\mu}}{\partial {\alpha}} +\frac{\partial {u^\mu}}{\partial {\alpha}} \right)e_\mu+\left(x^\mu+u^\mu\right)\frac{\partial {e_\mu}}{\partial {\alpha}} \right)\cdot\left( \left(\frac{\partial {x_\nu}}{\partial {\beta}} +\frac{\partial {u_\nu}}{\partial {\beta}} \right)e^\nu+\left(x_\nu+u_\nu\right)\frac{\partial {e^\nu}}{\partial {\beta}} \right) \\ &= \sum_{\alpha, \beta}d\alpha d\beta \left(\left(\frac{\partial {x^\mu}}{\partial {\alpha}} +\frac{\partial {u^\mu}}{\partial {\alpha}} \right)\left(\frac{\partial {x_\mu}}{\partial {\beta}} +\frac{\partial {u_\mu}}{\partial {\beta}} \right)+\left(x^\mu+u^\mu\right)\left(x_\nu+u_\nu\right)\frac{\partial {e_\mu}}{\partial {\alpha}} \cdot\frac{\partial {e^\nu}}{\partial {\beta}} +2\left(x^\mu+u^\mu\right)e^\nu\cdot\frac{\partial {e_\mu}}{\partial {\alpha}} \left(\frac{\partial {x_\nu}}{\partial {\beta}} +\frac{\partial {u_\nu}}{\partial {\beta}} \right)\right).\end{aligned}

Taking the difference we find

\begin{aligned}\begin{aligned}&(d\mathbf{u} + d\mathbf{x})^2 - d\mathbf{x}^2 \\ &=\sum_{\alpha, \beta}d\alpha d\beta \left( \frac{\partial {u^\mu}}{\partial {\alpha}} \frac{\partial {u_\mu}}{\partial {\beta}} +2\frac{\partial {u^\mu}}{\partial {\alpha}} \frac{\partial {x_\mu}}{\partial {\beta}} + \left(u^\mu u_\nu +x^\mu u_\nu +u^\mu x_\nu \right)\frac{\partial {e_\mu}}{\partial {\alpha}}\cdot\frac{\partial {e^\nu}}{\partial {\beta}} +2 \left(\frac{\partial {x^\mu}}{\partial {\alpha}}u_\nu+\frac{\partial {u^\mu}}{\partial {\alpha}}(x_\nu+u_\nu)\right)e_\mu \cdot \frac{\partial {e^\nu}}{\partial {\beta}}\right).\end{aligned}\end{aligned} \hspace{\stretch{1}}(3.49)

To evaluate this, it is useful, albeit messier, to group terms a bit

\begin{aligned}\begin{aligned}&(d\mathbf{u} + d\mathbf{x})^2 - d\mathbf{x}^2 \\ &=\sum_{\alpha}2 d\alpha d\alpha \left( \frac{1}{{2}}\frac{\partial {u^\mu}}{\partial {\alpha}} \frac{\partial {u_\mu}}{\partial {\alpha}} +\frac{\partial {u^\mu}}{\partial {\alpha}} \frac{\partial {x_\mu}}{\partial {\alpha}} + \frac{1}{{2}}\left(u^\mu u_\nu +x^\mu u_\nu +u^\mu x_\nu \right)\frac{\partial {e_\mu}}{\partial {\alpha}}\cdot\frac{\partial {e^\nu}}{\partial {\alpha}} +\left(\frac{\partial {x^\mu}}{\partial {\alpha}}u_\nu+\frac{\partial {u^\mu}}{\partial {\alpha}}(x_\nu+u_\nu)\right)e_\mu \cdot \frac{\partial {e^\nu}}{\partial {\alpha}}\right) \\ &+\sum_{\alpha < \beta}2 d\alpha d\beta \left( \frac{\partial {u^\mu}}{\partial {\alpha}} \frac{\partial {u_\mu}}{\partial {\beta}} +\frac{\partial {u^\mu}}{\partial {\alpha}} \frac{\partial {x_\mu}}{\partial {\beta}} +\frac{\partial {u^\mu}}{\partial {\beta}} \frac{\partial {x_\mu}}{\partial {\alpha}} + \frac{1}{{2}}\left(u^\mu u_\nu +x^\mu u_\nu +u^\mu x_\nu \right)\left(\frac{\partial {e_\mu}}{\partial {\alpha}}\cdot\frac{\partial {e^\nu}}{\partial {\beta}} +\frac{\partial {e_\mu}}{\partial {\beta}}\cdot\frac{\partial {e^\nu}}{\partial {\alpha}} \right) \right) \\ &+\sum_{\alpha < \beta}2 d\alpha d\beta \left( \left(\frac{\partial {x^\mu}}{\partial {\alpha}}u_\nu+\frac{\partial {u^\mu}}{\partial {\alpha}}(x_\nu+u_\nu)\right)e_\mu \cdot \frac{\partial {e^\nu}}{\partial {\beta}}+\left(\frac{\partial {x^\mu}}{\partial {\beta}}u_\nu+\frac{\partial {u^\mu}}{\partial {\beta}}(x_\nu+u_\nu)\right)e_\mu \cdot \frac{\partial {e^\nu}}{\partial {\alpha}}\right)\end{aligned}\end{aligned} \hspace{\stretch{1}}(3.50)

Here \alpha < \beta is used to denote summation over the pairs \alpha \ne \beta just once, not neccessarily any numeric ordering. For example with \alpha, \beta \in \{r, \phi, z\}, this could be the set \{\alpha, \beta\} \in \{r \phi, \phi z, z r\}.

Cartesian tensor.

In the Cartesian case all the partials of the unit vectors are zero, and we also have no need of upper or lower indexes. We are left with just

\begin{aligned}(d\mathbf{u} + d\mathbf{x})^2 - d\mathbf{x}^2 =\sum_{i, j, k}dx^idx^j\left( \frac{\partial {u^k}}{\partial {x^i}} \frac{\partial {u^k}}{\partial {x^j}} +2\frac{\partial {u^k}}{\partial {x^i}} \frac{\partial {x^k}}{\partial {x^j}} \right)\end{aligned} \hspace{\stretch{1}}(3.51)

However, since we also have {\partial {x^k}}/{\partial {x^j}} = \delta_{jk}, this is

\begin{aligned}(d\mathbf{u} + d\mathbf{x})^2 - d\mathbf{x}^2 =\sum_{i, j}2dx^idx^j\left( \frac{1}{{2}}\sum_k\frac{\partial {u^k}}{\partial {x^i}} \frac{\partial {u^k}}{\partial {x^j}} +\frac{\partial {u^j}}{\partial {x^i}} \right).\end{aligned} \hspace{\stretch{1}}(3.52)

This essentially recovers the result 3.11 derived in class.

Cylindrial tensor.

Now lets do the cylindrical tensor again, but this time without resorting mathematica brute force.

First we recall that all our basis vector derivatives are zero except for the \phi derivatives, and for those we have

\begin{aligned}\frac{\partial {\hat{\mathbf{r}}}}{\partial {\phi}} &= \hat{\boldsymbol{\phi}} \\ \frac{\partial {\hat{\boldsymbol{\theta}}}}{\partial {\phi}} &= -\hat{\mathbf{r}}.\end{aligned} \hspace{\stretch{1}}(3.53)

If we write

\begin{aligned}\mathbf{x} = r \hat{\mathbf{r}} + z \hat{\mathbf{z}} = x_r \hat{\mathbf{r}} + x_\phi \hat{\boldsymbol{\phi}} + x_z \hat{\mathbf{z}}\end{aligned} \hspace{\stretch{1}}(3.55)

We have for all the 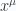x^\mu partials

\begin{aligned}\frac{\partial {x^\mu}}{\partial {\alpha}} = \left\{\begin{array}{l l}1 & \quad \mbox{if latex \alpha = x^\mu = r$ or \alpha = x^\mu = z} \\ 0 & \quad \mbox{otherwise}\end{array}\right.\end{aligned} \hspace{\stretch{1}}(3.56)$

We are now set to evaluate the terms in the sum of 3.50 for the cylindrical coordinate system and shouldn’t need Mathematica to do it. Let’s do this one at a time, starting with all the squared differential pairs. Those are, for \alpha \in \{r, \phi, z\} the value of

\begin{aligned}2 d\alpha d\alpha \left( \frac{1}{{2}}\frac{\partial {u_m}}{\partial {\alpha}} \frac{\partial {u_m}}{\partial {\alpha}} +\frac{\partial {u_m}}{\partial {\alpha}} \frac{\partial {x_m}}{\partial {\alpha}} + \frac{1}{{2}}\left(u_m u_n +x_m u_n +u_m x_n \right)\frac{\partial {e_m}}{\partial {\alpha}}\cdot\frac{\partial {e_n}}{\partial {\alpha}} +\left(\frac{\partial {x_m}}{\partial {\alpha}}u_n+\frac{\partial {u_m}}{\partial {\alpha}}(x_n+u_n)\right)e_m \cdot \frac{\partial {e_n}}{\partial {\alpha}}\right)\end{aligned} \hspace{\stretch{1}}(3.60)

For both r and z all our unit vectors have zero derivatives so we are left respectively with

\begin{aligned}2 dr dr \left( \frac{1}{{2}}\frac{\partial {u_m}}{\partial {r}} \frac{\partial {u_m}}{\partial {r}} +\frac{\partial {u_r}}{\partial {r}} \right),\end{aligned} \hspace{\stretch{1}}(3.60)

and

\begin{aligned}2 dz dz \left( \frac{1}{{2}}\frac{\partial {u_m}}{\partial {z}} \frac{\partial {u_m}}{\partial {z}} +\frac{\partial {u_z}}{\partial {z}} \right).\end{aligned} \hspace{\stretch{1}}(3.60)

For the \alpha = \phi term we have

\begin{aligned}&2 d\phi d\phi \left( \frac{1}{{2}}\frac{\partial {u_m}}{\partial {\phi}} \frac{\partial {u_m}}{\partial {\phi}} + \frac{1}{{2}}\sum_{m = r, \phi}\left(u_m u_m +2 x_m u_m \right)+\sum_{m n \in \{r \phi, \phi r\}}\left(\frac{\partial {x_m}}{\partial {\phi}}u_n+\frac{\partial {u_m}}{\partial {\phi}}(x_n+u_n)\right)e_m \cdot \frac{\partial {e_n}}{\partial {\phi}}\right) \\ &=2 d\phi d\phi \left( \frac{1}{{2}}\frac{\partial {u_m}}{\partial {\phi}} \frac{\partial {u_m}}{\partial {\phi}} + \frac{1}{{2}} \left( u_r^2 + u_\phi^2 \right) + r u_r-\frac{\partial {u_r}}{\partial {\phi}}u_\phi+\frac{\partial {u_\phi}}{\partial {\phi}}(r+u_r)\right)\end{aligned}

Now, on to the mixed terms. The easiest is the dz dr term, for which all the unit vector derivatives are zero, and we are left with just

\begin{aligned}2 dz dr \left( \frac{\partial {u_m}}{\partial {z}} \frac{\partial {u_m}}{\partial {r}} +\frac{\partial {u_m}}{\partial {z}} \frac{\partial {x_m}}{\partial {r}} +\frac{\partial {u_m}}{\partial {r}} \frac{\partial {x_m}}{\partial {z}} \right)=2 dz dr \left( \frac{\partial {u_m}}{\partial {z}} \frac{\partial {u_m}}{\partial {r}} +\frac{\partial {u_r}}{\partial {z}} +\frac{\partial {u_z}}{\partial {r}} \right)\end{aligned}

Now we have the two messy mixed terms. For the r, \phi term we get

\begin{aligned}&2 dr d\phi \left( \frac{\partial {u_m}}{\partial {r}} \frac{\partial {u_m}}{\partial {\phi}} +\frac{\partial {u_m}}{\partial {r}} \not{{\frac{\partial {x_m}}{\partial {\phi}}}}+\frac{\partial {u_m}}{\partial {\phi}} \frac{\partial {x_m}}{\partial {r}} + \frac{1}{{2}}\left(u_m u_n +x_m u_n +u_m x_n \right)\left(\not{{\frac{\partial {e_m}}{\partial {r}}}}\cdot\frac{\partial {e_n}}{\partial {\phi}} +\frac{\partial {e_m}}{\partial {\phi}}\cdot\not{{\frac{\partial {e_n}}{\partial {r}} }}\right) \right) \\ &+2 dr d\phi \left( \left(\frac{\partial {x_m}}{\partial {r}}u_n+\frac{\partial {u_m}}{\partial {r}}(x_n+u_n)\right)e_m \cdot \frac{\partial {e_n}}{\partial {\phi}}+\left(\frac{\partial {x_m}}{\partial {\phi}}u_n+\frac{\partial {u_m}}{\partial {\phi}}(x_n+u_n)\right)e_m \cdot \not{{\frac{\partial {e_n}}{\partial {r}}}}\right) \\ &=2 dr d\phi \left( \frac{\partial {u_m}}{\partial {r}} \frac{\partial {u_m}}{\partial {\phi}} +\frac{\partial {u_r}}{\partial {\phi}} +u_n\hat{\mathbf{r}} \cdot \frac{\partial {e_n}}{\partial {\phi}}+\frac{\partial {u_m}}{\partial {r}}(x_n+u_n)e_m \cdot \frac{\partial {e_n}}{\partial {\phi}}\right) \\ &=2 dr d\phi \left( \frac{\partial {u_m}}{\partial {r}} \frac{\partial {u_m}}{\partial {\phi}} +\frac{\partial {u_r}}{\partial {\phi}} -u_\phi+\frac{\partial {u_r}}{\partial {r}}(x_n+u_n)\hat{\mathbf{r}} \cdot \frac{\partial {e_n}}{\partial {\phi}}+\frac{\partial {u_\phi}}{\partial {r}}(x_n+u_n)\hat{\boldsymbol{\phi}} \cdot \frac{\partial {e_n}}{\partial {\phi}}\right) \\ &=2 dr d\phi \left( \frac{\partial {u_m}}{\partial {r}} \frac{\partial {u_m}}{\partial {\phi}} +\frac{\partial {u_r}}{\partial {\phi}} -u_\phi-\frac{\partial {u_r}}{\partial {r}}u_\phi+\frac{\partial {u_\phi}}{\partial {r}}(r +u_r)\right) \\ \end{aligned}

Finally for the z, \phi term we have

\begin{aligned}&2 dz d\phi \left( \frac{\partial {u_m}}{\partial {z}} \frac{\partial {u_m}}{\partial {\phi}} +\frac{\partial {u_m}}{\partial {z}} \not{{\frac{\partial {x_m}}{\partial {\phi}} }}+\frac{\partial {u_m}}{\partial {\phi}} \frac{\partial {x_m}}{\partial {z}} + \frac{1}{{2}}\left(u_m u_n +x_m u_n +u_m x_n \right)\left(\not{{\frac{\partial {e_m}}{\partial {z}}}}\cdot\frac{\partial {e_n}}{\partial {\phi}} +\frac{\partial {e_m}}{\partial {\phi}}\cdot\not{{\frac{\partial {e_n}}{\partial {z}} }}\right) \right) \\ &+2 d\phi dz \left( \left(\frac{\partial {x_m}}{\partial {z}}u_n+\frac{\partial {u_m}}{\partial {z}}(x_n+u_n)\right)e_m \cdot \frac{\partial {e_n}}{\partial {\phi}}+\left(\frac{\partial {x_m}}{\partial {\phi}}u_n+\frac{\partial {u_m}}{\partial {\phi}}(x_n+u_n)\right)e_m \cdot \not{{\frac{\partial {e_n}}{\partial {z}}}}\right) \\ &=2 dz d\phi \left( \frac{\partial {u_m}}{\partial {z}} \frac{\partial {u_m}}{\partial {\phi}} +\frac{\partial {u_m}}{\partial {\phi}} \frac{\partial {x_m}}{\partial {z}} +\not{{u_n\hat{\mathbf{z}} \cdot \frac{\partial {e_n}}{\partial {\phi}}}}+\frac{\partial {u_m}}{\partial {z}}(x_n+u_n)e_m \cdot \frac{\partial {e_n}}{\partial {\phi}}\right) \\ &=2 dz d\phi \left( \frac{\partial {u_m}}{\partial {z}} \frac{\partial {u_m}}{\partial {\phi}} +\frac{\partial {u_z}}{\partial {\phi}} -\frac{\partial {u_r}}{\partial {z}}u_\phi+\frac{\partial {u_\phi}}{\partial {z}}(r+u_r)\right) \\ \end{aligned}

To summarize we have, including both first and second order terms,

\begin{aligned}\begin{aligned}{d\mathbf{l}'}^2 - d\mathbf{x}^2&=2 dr dr \left( \frac{1}{{2}}\frac{\partial {u_m}}{\partial {r}} \frac{\partial {u_m}}{\partial {r}} +\frac{\partial {u_r}}{\partial {r}} \right) \\ &+2 r^2 d\phi d\phi \left( \frac{1}{{2 r^2}}\frac{\partial {u_m}}{\partial {\phi}} \frac{\partial {u_m}}{\partial {\phi}} + \frac{1}{{2 r^2}} \left( u_r^2 + u_\phi^2 \right) + \frac{u_r}{r}-\frac{1}{{r}}\frac{\partial {u_r}}{\partial {\phi}}\frac{u_\phi}{r}+\frac{1}{{r}}\frac{\partial {u_\phi}}{\partial {\phi}}\left(1+\frac{u_r}{r}\right)\right) \\ &+2 dz dz \left( \frac{1}{{2}}\frac{\partial {u_m}}{\partial {z}} \frac{\partial {u_m}}{\partial {z}} +\frac{\partial {u_z}}{\partial {z}} \right) \\ &+2 dr r d\phi \left( \frac{\partial {u_m}}{\partial {r}} \frac{1}{{r}}\frac{\partial {u_m}}{\partial {\phi}} +\frac{1}{{r}}\frac{\partial {u_r}}{\partial {\phi}} -\frac{u_\phi}{r}-\frac{\partial {u_r}}{\partial {r}}\frac{u_\phi}{r}+\frac{\partial {u_\phi}}{\partial {r}}\left(1 +\frac{u_r}{r}\right)\right) \\ &+2 r d\phi dz \left( \frac{\partial {u_m}}{\partial {z}} \frac{1}{{r}}\frac{\partial {u_m}}{\partial {\phi}} +\frac{1}{{r}}\frac{\partial {u_z}}{\partial {\phi}} -\frac{\partial {u_r}}{\partial {z}}\frac{u_\phi}{r}+\frac{\partial {u_\phi}}{\partial {z}}\left(1+\frac{u_r}{r}\right)\right) \\ &+2 dz dr \left( \frac{\partial {u_m}}{\partial {z}} \frac{\partial {u_m}}{\partial {r}} +\frac{\partial {u_r}}{\partial {z}} +\frac{\partial {u_z}}{\partial {r}} \right)\end{aligned}\end{aligned} \hspace{\stretch{1}}(3.60)

Factors of r have been pulled out so that the portions remaining in the braces are exactly the cylindrical tensor elements as given in the text (except also with the second order terms here). Observe that the pre-calculation of the general formula has allowed an on paper expansion of the cylindrical tensor without too much pain, and this time without requiring Mathematica.

Spherical tensor.

FIXME: TODO.

References

[1] L.D. Landau, EM Lifshitz, JB Sykes, WH Reid, and E.H. Dill. Theory of elasticity: Vol. 7 of course of theoretical physics. Physics Today, 13:44, 1960.

Posted in Math and Physics Learning. | Tagged: , , , , , , , | Leave a Comment »

PHY454H1S Continuum Mechanics. Lecture 3. Strain tensor review. Stress tensor. Taught by Prof. K. Das.

Posted by peeterjoot on January 20, 2012

[Click here for a PDF of this post with nicer formatting and figures if the post had any (especially if my latex to wordpress script has left FORMULA DOES NOT PARSE errors.)]

Disclaimer.

Peeter’s lecture notes from class. May not be entirely coherent.

Review. Strain.

Strain is the measure of stretching. This is illustrated pictorially in figure (\ref{fig:continuumL3:continuumL3fig1})
\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{continuumL3fig1}
\caption{Stretched line elements.}
\end{figure}

\begin{aligned}{ds'}^2 - ds^2 = 2 e_{ik} dx_i dx_k,\end{aligned} \hspace{\stretch{1}}(1.1)

where e_{ik} is the strain tensor. We found

\begin{aligned}e_{ik} = \frac{1}{{2}} \left( \frac{\partial {e_i}}{\partial {x_k}} +\frac{\partial {e_k}}{\partial {x_i}} +\frac{\partial {e_l}}{\partial {x_i}} \frac{\partial {e_l}}{\partial {x_k}} \right)\end{aligned} \hspace{\stretch{1}}(1.2)

Why do we have a factor two? Observe that if the deformation is small we can write

\begin{aligned}{ds'}^2 - ds^2 &= (ds' - ds)(ds' + ds) \\ &\approx (ds' - ds) 2 ds\end{aligned}

so that we find

\begin{aligned}\frac{{ds'}^2 - ds^2 }{ds^2}\approx\frac{ds' - ds }{ds}\end{aligned} \hspace{\stretch{1}}(1.3)

Suppose for example, that we have a diagonalized strain tensor, then we find

\begin{aligned}{ds'}^2 - ds^2 = 2 e_{ii} \left(\frac{dx_i}{ds}\right)^2\end{aligned} \hspace{\stretch{1}}(1.4)

so that

\begin{aligned}\frac{{ds'}^2 - ds^2 }{ds^2}= 2 e_{ii} dx_i^2\end{aligned} \hspace{\stretch{1}}(1.5)

Observe that here again we see this factor of two.

If we have a diagonalized strain tensor, the tensor is of the form

\begin{aligned}\begin{bmatrix}e_{11} & 0 & 0 \\ 0 & e_{22} & 0 \\ 0 & 0 & e_{33} \end{bmatrix}\end{aligned} \hspace{\stretch{1}}(1.6)

we have

\begin{aligned}{dx_i'}^2 - dx_i^2 = 2 e_{ii} dx_i^2\end{aligned} \hspace{\stretch{1}}(1.7)

\begin{aligned}{ds'}^2 = (1 + 2 e_{11}) dx_1^2+(1 + 2 e_{22}) dx_2^2+(1 + 2 e_{33}) dx_3^2\end{aligned} \hspace{\stretch{1}}(1.8)

\begin{aligned}ds^2 = dx_1^2+dx_2^2+dx_3^2\end{aligned} \hspace{\stretch{1}}(1.9)

so

\begin{aligned}dx_1' &= \sqrt{1 + 2 e_{11}} dx_1 \sim ( 1 + e_{11}) dx_1 \\ dx_2' &= \sqrt{1 + 2 e_{22}} dx_2 \sim ( 1 + e_{22}) dx_2 \\ dx_3' &= \sqrt{1 + 2 e_{33}} dx_3 \sim ( 1 + e_{33}) dx_3\end{aligned} \hspace{\stretch{1}}(1.10)

Observe that the change in the volume element becomes the trace

\begin{aligned}dV' = dx_1'dx_2'dx_3'= dV(1 + e_{ii})\end{aligned} \hspace{\stretch{1}}(1.13)

How do we use this? Suppose that you are given a strain tensor. This should allow you to compute the stretch in any given direction.

FIXME: find problem and try this.

Stress tensor.

Reading for this section is section 2 from the text associated with the prepared notes [1].

We’d like to consider a macroscopic model that contains the net effects of all the internal forces in the object as depicted in figure (\ref{fig:continuumL3:continuumL3fig2})

\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{continuumL3fig2}
\caption{Internal forces.}
\end{figure}

We will consider a volume big enough that we won’t have to consider the individual atomic interactions, only the average effects of those interactions. Will will look at the force per unit volume on a differential volume element

The total force on the body is

\begin{aligned}\iiint \mathbf{F} dV,\end{aligned} \hspace{\stretch{1}}(2.14)

where \mathbf{F} is the force per unit volume. We will evaluate this by utilizing the divergence theorem. Recall that this was

\begin{aligned}\iiint (\boldsymbol{\nabla} \cdot \mathbf{A}) dV= \iint \mathbf{A} \cdot d\mathbf{s}\end{aligned} \hspace{\stretch{1}}(2.15)

We have a small problem, since we have a non-divergence expression of the force here, and it is not immediately obvious that we can apply the divergence theorem. We can deal with this by assuming that we can find a vector valued tensor, so that if we take the divergence of this tensor, we end up with the force. We introduce the quantity

\begin{aligned}\mathbf{F} = \frac{\partial {\sigma_{ik}}}{\partial {x_k}},\end{aligned} \hspace{\stretch{1}}(2.16)

and require this to be a vector. We can then apply the divergence theorem

\begin{aligned}\iiint \mathbf{F} dV = \iiint \frac{\partial {\sigma_{ik}}}{\partial {x_k}} d\mathbf{x}^3 \iint \sigma_{ik} ds_k,\end{aligned} \hspace{\stretch{1}}(2.17)

where ds_k is a surface element. We identify this tensor

\begin{aligned}\sigma_{ik} = \frac{\text{Force}}{\text{Unit Area}}\end{aligned} \hspace{\stretch{1}}(2.18)

and

\begin{aligned}f_i = \sigma_{ik} ds_k,\end{aligned} \hspace{\stretch{1}}(2.19)

as the force on the surface element ds_k. In two dimensions this is illustrated in the following figures (\ref{fig:continuumL3:continuumL3fig3})
\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{continuumL3fig3}
\caption{2D strain tensor.}
\end{figure}

Observe that we use the index i above as the direction of the force, and index k as the direction normal to the surface.

Note that the strain tensor has the matrix form

\begin{aligned}\begin{bmatrix}\sigma_{11} & \sigma_{12} & \sigma_{13} \\ \sigma_{21} & \sigma_{22} & \sigma_{23} \\ \sigma_{31} & \sigma_{32} & \sigma_{33}\end{bmatrix}\end{aligned} \hspace{\stretch{1}}(2.20)

We will show later that this tensor is in fact symmetric.

FIXME: given some 3D forces, compute the stress tensor that is associated with it.

Examples of the stress tensor

Example 1. stretch in two opposing directions.

\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{continuumL3fig4}
\caption{Opposing stresses in one direction.}
\end{figure}

Here, as illustrated in figure (\ref{fig:continuumL3:continuumL3fig4}), the associated (2D) stress tensor takes the simple form

\begin{aligned}\begin{bmatrix}\sigma_{11} & 0 \\ 0 & 0\end{bmatrix}\end{aligned} \hspace{\stretch{1}}(2.21)

Example 2. stretch in a pair of mutually perpendicular directions

For a pair of perpendicular forces applied in two dimensions, as illustrated in figure (\ref{fig:continuumL3:continuumL3fig5})
\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{continuumL3fig5}
\caption{Mutually perpendicular forces}
\end{figure}

our stress tensor now just takes the form

\begin{aligned}\begin{bmatrix}\sigma_{11} & 0 \\ 0 & \sigma_{22}\end{bmatrix}\end{aligned} \hspace{\stretch{1}}(2.22)

It’s easy to imagine now how to get some more general stress tensors, should we make a change of basis that rotates our frame.

Example 3. radial stretch

Suppose we have a fire fighter’s safety net, used to catch somebody jumping from a burning building (do they ever do that outside of movies?), as in figure (\ref{fig:continuumL3:continuumL3fig6}). Each of the firefighters contributes to the stretch.

\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{continuumL3fig6}
\caption{Radial forces.}
\end{figure}

FIXME: what form would the tensor take for this? Would we have to use a radial form of the tensor? What would that be?

References

[1] L.D. Landau, EM Lifshitz, JB Sykes, WH Reid, and E.H. Dill. Theory of elasticity: Vol. 7 of course of theoretical physics. Physics Today, 13:44, 1960.

Posted in Math and Physics Learning. | Tagged: , , , | Leave a Comment »

« Previous Entries