Geometric Algebra. The very quickest introduction.

[Click here for a PDF of this post with nicer formatting.]

Motivation.

An attempt to make a relatively concise introduction to Geometric (or Clifford) Algebra. Much more complete introductions to the subject can be found in [1], [2], and [3].

Axioms

We have a couple basic principles upon which the algebra is based

1. Vectors can be multiplied.
2. The square of a vector is the (squared) length of that vector (with appropriate generalizations for non-Euclidean metrics).
3. Vector products are associative (but not necessarily commutative).

That’s really all there is to it, and the rest, paraphrasing Feynman, can be figured out by anybody sufficiently clever.

By example. The 2D case.

Consider a 2D Euclidean space, and the product of two vectors and in that space. Utilizing a standard orthonormal basis we can write

and let’s write out the product of these two vectors , not yet knowing what we will end up with. That is

From axiom 2 we have , so we have

We’ve multiplied two vectors and ended up with a scalar component (and recognize that this part of the vector product is the dot product), and a component that is a “something else”. We’ll call this something else a bivector, and see that it is characterized by a product of non-colinear vectors. These products and are in fact related, and we can see that by looking at the case of . For that we have

Since axiom (2) requires our vectors square to equal its (squared) length, we must then have

or

We see that Euclidean orthonormal vectors anticommute. What we can see with some additional study is that any colinear vectors commute, and in Euclidean spaces (of any dimension) vectors that are normal to each other anticommute (this can also be taken as a definition of normal).

We can now return to our product of two vectors 3.3 and simplify it slightly

The product of two vectors in 2D is seen here to have one scalar component, and one bivector component (an irreducible product of two normal vectors). Observe the symmetric and antisymmetric split of the scalar and bivector components above. This symmetry and antisymmetry can be made explicit, introducing dot and wedge product notation respectively

so that the vector product can be written as

Pseudoscalar

In many contexts it is useful to introduce an ordered product of all the unit vectors for the space is called the pseudoscalar. In our 2D case this is

a quantity that we find behaves like the complex imaginary. That can be shown by considering its square

Here the anticommutation of normal vectors property has been used, as well as (for the first time) the associative multiplication axiom.

In a 3D context, you’ll see the pseudoscalar in many places (expressing the normals to planes for example). It also shows up in a number of fundamental relationships. For example, if one writes

for the 3D pseudoscalar, then it’s also possible to show

something that will be familiar to the student of QM, where we see this in the context of Pauli matrices. The Pauli matrices also encode a Clifford algebraic structure, but we do not need an explicit matrix representation to do so.

Rotations

Very much like complex numbers we can utilize exponentials to perform rotations. Rotating in a sense from to , can be expressed as

More generally, even in N dimensional Euclidean spaces, if is a vector in a plane, and and are perpendicular unit vectors in that plane, then the rotation through angle is given by

This is illustrated in figure (1).

Plane rotation.

 

Notice that we have expressed the rotation here without utilizing a normal direction for the plane. The sense of the rotation is encoded by the bivector that describes the plane and the orientation of the rotation (or by duality the direction of the normal in a 3D space). By avoiding a requirement to encode the rotation using a normal to the plane we have an method of expressing the rotation that works not only in 3D spaces, but also in 2D and greater than 3D spaces, something that isn’t possible when we restrict ourselves to traditional vector algebra (where quantities like the cross product can’t be defined in a 2D or 4D space, despite the fact that things they may represent, like torque are planar phenomena that do not have any intrinsic requirement for a normal that falls out of the plane.).

When does not lie in the plane spanned by the vectors and , as in figure (2), we must express the rotations differently. A rotation then takes the form

3D rotation.

 

In the 2D case, and when the vector lies in the plane this reduces to the one sided complex exponential operator used above. We see these types of paired half angle rotations in QM, and they are also used extensively in computer graphics under the guise of quaternions.

References

[1] L. Dorst, D. Fontijne, and S. Mann. Geometric Algebra for Computer Science. Morgan Kaufmann, San Francisco, 2007.

[2] C. Doran and A.N. Lasenby. Geometric algebra for physicists. Cambridge University Press New York, Cambridge, UK, 1st edition, 2003.

[3] D. Hestenes. New Foundations for Classical Mechanics. Kluwer Academic Publishers, 1999.

Derivation of the spherical polar Laplacian

[Click here for a PDF of this post with nicer formatting]

Motivation.

In [1] was a Geometric Algebra derivation of the 2D polar Laplacian by squaring the quadient. In [2] was a factorization of the spherical polar unit vectors in a tidy compact form. Here both these ideas are utilized to derive the spherical polar form for the Laplacian, an operation that is strictly algebraic (squaring the gradient) provided we operate on the unit vectors correctly.

Our rotation multivector.

Our starting point is a pair of rotations. We rotate first in the plane by

Then apply a rotation in the plane

The composition of rotations now gives us

Expressions for the unit vectors.

The unit vectors in the rotated frame can now be calculated. With we can calculate

Performing these we get

and

and

Summarizing these are

Derivatives of the unit vectors.

We’ll need the partials. Most of these can be computed from 3.9 by inspection, and are

Expanding the Laplacian.

We note that the line element is , so our gradient in spherical coordinates is

We can now evaluate the Laplacian

Evaluating these one set at a time we have

and

and

Summing these we have

This is often written with a chain rule trick to considate the and partials

It’s simple to verify that this is identical to 5.23.

References

[1] Peeter Joot. Polar form for the gradient and Laplacian. [online]. http://sites.google.com/site/peeterjoot/math2009/polarGradAndLaplacian.pdf.

[2] Peeter Joot. Spherical Polar unit vectors in exponential form. [online]. http://sites.google.com/site/peeterjoot/math2009/sphericalPolarUnit.pdf .

On Professor Dmitrevsky’s “the only valid Laplacian definition is the divergence of gradient”.

[Click here for a PDF of this post with nicer formatting]

Dedication.

To all tyrannical old Professors driven to cruelty by an unending barrage of increasingly ill prepared students.

Motivation.

The text [1] has an excellent general derivation of a number of forms of the gradient, divergence, curl and Laplacian.

This is actually done, not starting with the usual Cartesian forms, but more general definitions.

These are then shown to imply the usual Cartesian definitions, plus provide the means to calculate the general relationships in whatever coordinate system you like. All in all one can’t beat this approach, and I’m not going to try to replicate it, because I can’t improve it in any way by doing so.

Given that, what do I have to say on this topic? Well, way way back in first year electricity and magnetism, my dictator of a prof, the intimidating but diminutive Dmitrevsky, yelled at us repeatedly that one cannot just dot the gradient to form the Laplacian. As far as he was concerned one can only say

and never never never, the busted way

Because “this only works in Cartesian coordinates”. He probably backed up this assertion with a heartwarming and encouraging statement like “back in the days when University of Toronto was a real school you would have learned this in kindergarten”.

This detail is actually something that has bugged me ever since, because my assumption was that, provided one was careful, why would a change to an alternate coordinate system matter? The gradient is still the gradient, so it seems to me that this ought to be a general way to calculate things.

Here we explore the validity of the dictatorial comments of Prof Dmitrevsky. The key to reconciling intuition and his statement turns out to lie with the fact that one has to let the gradient operate on the unit vectors in the non Cartesian representation as well as the partials, something that wasn’t clear as a first year student. Provided that this is done, the plain old dot product procedure yields the expected results.

This exploration will utilize a two dimensional space as a starting point, transforming from Cartesian to polar form representation. I’ll also utilize a geometric algebra representation of the polar unit vectors.

The gradient in polar form.

Lets start off with a calculation of the gradient in polar form starting with the Cartesian form. Writing , , , and , we want to map

into the same form using , and . With we have

Next we need to do a chain rule expansion of the partial operators to change variables. In matrix form that is

To calculate these partials we drop back to coordinates

From this we calculate

for

We can now write down the gradient in polar form, prior to final simplification

Observe that we can factor a unit vector

so the element of the matrix product in the interior is

Similarly, the element of the matrix product in the interior is

The exponentials cancel nicely, leaving after a final multiplication with the polar form for the gradient

That was a fun way to get the result, although we could have just looked it up. We want to use this now to calculate the Laplacian.

Polar form Laplacian for the plane.

We are now ready to look at the Laplacian. First let’s do it the first year electricity and magnetism course way. We look up the formula for polar form divergence, the one we were supposed to have memorized in kindergarten, and find it to be

We can now apply this to the gradient vector in polar form which has components , and , and get

This is the expected result, and what we should get by performing in polar form. Now, let’s do it the wrong way, dotting our gradient with itself.

This is wrong! So is Dmitrevsky right that this procedure is flawed, or do you spot the mistake? I have also cruelly written this out in a way that obscures the error and highlights the source of the confusion.

The problem is that our unit vectors are functions, and they must also be included in the application of our partials. Using the coordinate polar form without explicitly putting in the unit vectors is how we go wrong. Here’s the right way

Now we need the derivatives of our unit vectors. The derivatives are zero since these have no radial dependence, but we do have partials

and

(One should be able to get the same results if these unit vectors were written out in full as , and , instead of using the obscure geometric algebra quaterionic rotation exponential operators.)

Having calculated these partials we now have

Exactly what it should be, and what we got with the coordinate form of the divergence operator when applying the “Laplacian equals the divergence of the gradient” rule blindly. We see that the expectation that is the Laplacian in more than the Cartesian coordinate system is not invalid, but that care is required to apply the chain rule to all functions. We also see that expressing a vector in coordinate form when the basis vectors are position dependent is also a path to danger.

Is this anything that our electricity and magnetism prof didn’t know? Unlikely. Is this something that our prof felt that could not be explained to a mob of first year students? Probably.

References

[1] F.W. Byron and R.W. Fuller. Mathematics of Classical and Quantum Physics. Dover Publications, 1992.

Spherical polar pendulum for one and multiple masses (Take II)

[Click here for a PDF of this post with nicer formatting]

Motivation

Attempting the multiple spherical pendulum problem with a bivector parameterized Lagrangian has just been attempted ([1]), but did not turn out to be an effective approach. Here a variation is used, employing regular plain old scalar spherical angle parameterized Kinetic energy, but still employing Geometric Algebra to express the Hermitian quadratic form associated with this energy term.

The same set of simplifying assumptions will be made. These are point masses, zero friction at the pivots and rigid nonspringy massless connecting rods between the masses.

The Lagrangian.

A two particle spherical pendulum is depicted in figure (\ref{fig:sPolarMultiPendulum:pendulumDouble})

\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.4\textheight]{pendulumDouble}
\caption{Double spherical pendulum.}
\end{figure}

The position vector for each particle can be expressed relative to the mass it is connected to (or the origin for the first particle), as in

To express the Kinetic energy for any of the masses , we need the derivative of the incremental difference in position

Introducing a Hermitian conjugation , reversing and transposing the matrix, and writing

We can now write the relative velocity differential as

Observe that the inner product is Hermitian under this definition since . \footnote{Realized later, and being too lazy to adjust everything in these notes, the use of reversion here is not neccessary. Since the generalized coordinates are scalars we could use transposition instead of Hermitian conjugation. All the matrix elements are vectors so reversal doesn’t change anything.}

The total (squared) velocity of the th particle is then

(where the zero matrix in is a by one zero). Summing over all masses and adding in the potential energy we have for the Lagrangian of the system

There’s a few layers of equations involved and we still have an unholy mess of matrix and geometric algebra in the kernel of the kinetic energy quadratic form, but at least this time all the generalized coordinates of the system are scalars.

Some tidy up.

Before continuing with evaluation of the Euler-Lagrange equations it is helpful to make a couple of observations about the structure of the matrix products that make up our velocity quadratic forms

Specifically, consider the products that make up the elements of the matrices . Without knowing anything about the grades that make up the elements of , since it is Hermitian (by this definition of Hermitian) there can be no elements of grade order two or three in the final matrix. This is because reversion of such grades inverts the sign, and the matrix elements in all equal their reverse. Additionally, the elements of the multivector column matrices are vectors, so in the product we can only have scalar and bivector (grade two) elements. The resulting one by one scalar matrix is a sum over all the mixed angular velocities , , and , so once this summation is complete any bivector grades of must cancel out. This is consistent with the expectation that we have a one by one scalar matrix result out of this in the end (i.e. a number). The end result is a freedom to exploit the convienence of explicitly using a scalar selection operator that filters out any vector, bivector, and trivector grades in the products . We will get the same result if we write

Pulling in the summation over we have

It appears justifiable to lable the factors of the angular velocity matrices as moments of inertia in a generalized sense. Using this block matrix form, and scalar selection, we can now write the Lagrangian in a slightly tidier form

After some expansion, writing , and so forth, one can find that the scalar parts of the block matrixes contained in are

The diagonal blocks are particularily simple and have no dependence

Observe also that , so the scalar matrix

is a real symmetric matrix. We have the option of using this explicit scalar expansion if desired for further computations associated with this problem. That completely eliminates the Geometric algebra from the problem, and is probably a logical way to formulate things for numerical work since one can then exploit any pre existing matrix algebra system without having to create one that understands non-commuting variables and vector products.

Evaluating the Euler-Lagrange equations.

For the acceleration terms of the Euler-Lagrange equations our computation reduces nicely to a function of only

and

The last groupings above made use of , and in particular . We can now form a column matrix putting all the angular velocity gradient in a tidy block matrix representation

A small aside on Hamiltonian form. This velocity gradient is also the conjugate momentum of the Hamiltonian, so if we wish to express the Hamiltonian in terms of conjugate momenta, we require invertability of at the point in time that we evaluate things. Writing

and noting that , we get for the kinetic energy portion of the Hamiltonian

Now, the invertability of cannot be taken for granted. Even in the single particle case we do not have invertability. For the single particle case we have

so at this quadratic form is singlular, and the planar angular momentum becomes a constant of motion.

Returning to the evaluation of the Euler-Lagrange equations, the problem is now reduced to calculating the right hand side of the following system

With back substituition of 22, and 24 we have a complete non-multivector expansion of the left hand side. For the right hand side taking the and derivatives respectively we get

So to procede we must consider the partials. A bit of thought shows that the matrices of partials above are mostly zeros. Illustrating by example, consider , which in block matrix form is

Observe that the diagonal term has a scalar plus its reverse, so we can drop the one half factor and one of the summands for a total contribution to of just

Now consider one of the pairs of off diagonal terms. Adding these we contributions to of

This has exactly the same form as the diagonal term, so summing over all terms we get for the position gradient components of the Euler-Lagrange equation just

The only thing that remains to do is evaluate the matrixes.

It should be possible but it is tedious to calculate the block matrix derivative terms from the partials using

However multiplying this out and reducing is a bit tedious and would be a better job for a symbolic algebra package. With 22 available to use, one gets easily

The right hand side of the Euler-Lagrange equations now becomes

Can the matrices be factored out, perhaps allowing for expression as a function of ? How to do that if it is possible is not obvious. The driving reason to do so would be to put things into a tidy form where things are a function of the system angular velocity vector , but this is not possible anyways since the gradient is non-linear.

Hamiltonian form and linearization.

Having calculated the Hamiltonian equations for the multiple mass planar pendulum in [2], doing so for the spherical pendulum can now be done by inspection. With the introduction of a phase space vector for the system using the conjugate momenta (for angles where these conjugate momenta are non-singlular)

we can write the Hamiltonian equations

The position gradient is given explicitly in 39, and that can be substituted here. That gradient is expressed in terms of and not the conjugate momenta, but the mapping required to express the whole system in terms of the conjugate momenta is simple enough

It is apparent that for any sort of numerical treatment use of a angular momentum and angular position phase space vector is not prudent. If the aim is nothing more than working with a first order system instead of second order, then we are probably better off with an angular velocity plus angular position phase space system.

This eliminates the requirement for inverting the sometimes singular matrix , but one is still left with something that is perhaps tricky to work with since we have the possibility of zeros on the left hand side. The resulting equation is of the form

where is a possibly singular matrix, and is a non-linear function of the components of , and . This is concievably linearizable in the neighbourhood of a particular phase space point . If that is done, resulting in an equation of the form

where and is an appropriate matrix of partials (the specifics of which don’t really have to be spelled out here). Because of the possible singularities of the exponentiation techniques applied to the linearized planar pendulum may not be possible with such a linearization. Study of this less well formed system of LDEs probably has interesting aspects, but is also likely best tackled independently of the specifics of the spherical pendulum problem.

Thoughts about the Hamiltonian singularity.

The fact that the Hamiltonian goes singular on the horizontal in this spherical polar representation is actually what I think is the most interesting bit in the problem (the rest being a lot mechanical details). On the horizontal or radians/sec makes no difference to the dynamics. All you can say is that the horizontal plane angular momentum is a constant of the system. It seems very much like the increasing uncertaintly that you get in the corresponding radial QM equation. Once you start pinning down the angle, you loose the ability to say much about .

It is also kind of curious how the energy of the system is never ill defined but a choice of a particular orientation to use as a reference for observations of the momenta introduces the singularity as the system approaches the horizontal in that reference frame.

Perhaps there are some deeper connections relating these classical and QM similarity. Would learning about symplectic flows and phase space volume invariance shed some light on this?

A summary.

A fair amount of notation was introduced along the way in the process of formulating the spherical pendulum equations. It is worthwhile to do a final consise summary of notation and results before moving on for future reference.

The positions of the masses are given by

With the introduction of a column vector of vectors (where we multiply matrices using the Geometric vector product),

and a matrix of velocity components (with matrix multiplication of the vector elements using the Geometric vector product), we can form the Lagrangian

An explicit scalar matrix evaluation of the (symmetric) block matrix components of was evaluated and found to be

These can be used if explicit evaluation of the Kinetic energy is desired, avoiding redundant summation over the pairs of skew entries in the quadratic form matrix

We utilize angular position and velocity gradients

and use these to form the Euler-Lagrange equations for the system in column vector form

For the canonical momenta we found the simple result

For the position gradient portion of the Euler-Lagrange equations 63 we found in block matrix form

A set of Hamiltonian equations for the system could also be formed. However, this requires that one somehow restrict attention to the subset of phase space where the canonical momenta matrix is non-singular, something not generally possible.

References

[1] Peeter Joot. {Spherical polar pendulum for one and multiple masses, and multivector Euler-Lagrange formulation.} [online]. http://sites.google.com/site/peeterjoot/math2009/sPolarMultiPendulum.pdf.

[2] Peeter Joot. Hamiltonian notes. [online]. http://sites.google.com/site/peeterjoot/math2009/hamiltonian.pdf.

Spherical polar pendulum for one and multiple masses, and multivector Euler-Lagrange formulation.

[Click here for a PDF of this post with nicer formatting]

Motivation

The planar multiple pendulum problem proved somewhat tractable in the Hamiltonian formulation. Generalizing this to allow for three dimensional motion is a logical next step. Here this is attempted, using a Geometric Algebra scalar plus bivector parametrization of the spherical position of each dangling mass relative to the position of what it is attached to, as in

The exponential is essentially a unit quaternion, rotating the vector from the polar axis to its angle dependent position. Two sided rotation operators are avoided here by requiring of the unit bivector , where is a vector in the plane of rotation passing through the great circle from 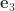through . Note that we are free to pick , the unit vector in the 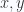plane at angle from the x-axis. When that is done since these are perpendicular. Setting up the Lagrangian in terms of the bivector 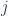instead of the scalar angle will be attempted, since this is expected to have some elegance and will be a fun way to try the problem. This should also provide a concrete example of a multivector Lagrangian in a context much simpler than electromagnetic fields or quantum mechanics.

Note finally that a number of simplifying assumptions will be made. These include use of point masses, zero friction at the pivots and rigid nonspringy massless connecting rods between the masses.

Kinetic energy for the single pendulum case.

Let’s compute derivatives of the unit vector

This can be done with both the left and right factorization of 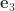, and are respectively

These derivatives have been grouped into a matrix factors that allow a natural seeming conjugate operation to be defined. That is for a matrix of multivector elements

define a conjugate matrix, as the transpose of the reversed elements

With this definition, plus two helpers

Our velocity becomes

Explicitly, expanding the inner matrix product we can write

This is a slightly unholy mix of geometric and matrix algebra, but it works to compactly express the velocity dependence. Observe that this inner matrix , so it is Hermitian with this definition of conjugation.

Our Lagrangian for the one particle pendulum, measuring potential energy from the horizontal, is then

We also have a mechanism that should generalize fairly easily to the two or many pendulum cases too.

Before continuing, it should be noted that there were assumptions made in this energy expression derivation that are not reflected in the Lagrangian above. One of these was the unit bivector assumption for 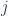, as well as a 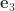containment assumption for the plane this represents (). So for completeness we should probably add to the Lagrangian above some Lagrange multiplier enforced constraints

Here has got to be a trivector multiplier for the Lagrangian to be a scalar. Can we get away with omitting these constraints?

Two and multi particle case.

Having constructed a way that can express the velocity of a single spherical pendulum in a tidy way, we can move on to consider the multiple pendulum case as shown in figure (\ref{fig:sPolarMultiPendulum:pendulumDouble})

\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.4\textheight]{pendulumDouble}
\caption{Double spherical pendulum.}
\end{figure}

There are two bivectors depicted, and representing oriented planes passing through great circles from a local polar axis (in direction 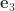). Let the positions of the respective masses be and , where each mass is connected by a rigid massless rod of length and respectively. The masses are rotated by angles and in the planes and from an initial direction of 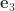. We can express the position of the second mass as

We can use the same factorization as previously used for the single mass case and write for our collection of angular velocities

Using this the total Kinetic energy is

Notation has been switched slightly from the single mass case, and the factor is now incorporated directly into for convenience.

An expansion of is essentially one of block matrix multiplication (where we already have to be careful with order of operations as we do for the geometric product elements themselves). We have something like

We have for the products

So our quadratic form matrix is

In general for the multiple particle case this is

Expanded explicitly this is

Observe that the order of products in this expansion is specifically ordered, since the and bivectors do not necessarily commute.

The potential in the multiple particle case is also fairly straightforward to compute. Consider the two particle case to illustrate the pattern. Using the lowest point as the potential reference we have

Alternately, dropping all the constant terms (using the horizon as the potential reference) we have for the general case

Lets collect all the bits and pieces now for the multiple pendulum Lagrangian now, repeating for coherency, and introducing a tiny bit more notation (mass sums and block angular velocity matrices) for convenience

Building up to the Multivector Euler-Lagrange equations.

Rather than diving right into any abstract math, lets consider a few specific examples of multivector Lagrangians to develop some comfort with non-scalar Lagrangian functions. The generalized “coordinates” in the Lagrangian for the spherical pendulum problem being considered include include bivectors, and we don’t know how to evaluate the Euler Lagrange equations for anything but scalar generalized coordinates.

The goal is to develop Euler-Lagrange equations that can handle a Lagrangian for these more general functions, but until we figure out how to do that, we can at least tackle the problem using variation of the action around a stationary solution.

A first example to build intuition.

To help understand what we have to do, lets consider the very simplest bivector parametrized Lagrangian, that of a spherical pendulum constrained (perhaps by a track or a surface) of moving only in a ring. This is shown pictorially in figure (\ref{fig:sPolarMultiPendulum:pendulumPolarCircular})

\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.4\textheight]{pendulumPolarCircular}
\caption{Circularly constrained spherical pendulum.}
\end{figure}

The potential energy is fixed on this surface, so our Lagrangian is purely kinetic

We’d like to directly vary the action for the Lagrangian around a stationary solution

Introducing a bivector variation , and writing we have

The first term is just . Setting the variation (neglecting the quadratic term) and integrating by parts we have

With arbitrary it appears that the solutions of the variation problem are given by

Has anything been lost by requiring that this is zero identically when all we had originally was the dot product of this with the variation bivector was zero? If this zero describes the solution set, then we should be able to integrate this, yielding a constant. However, following this to its logical conclusion leads to inconsistency. Integrating 46, producing a bivector constant we have

The original constraint on 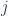was the bivector spanning the plane from the polar axis to the azimuthal unit vector in the 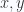plane at angle a . The dependence wasn’t specified, and left encoded in the bivector representation. Without words that was

Inserting back into 47 this gives

One more integration is trivially possible yielding

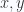There are two possibilities for the grades of , one is , so that the time dependence is a scalar, and the other is so that we have an plane bivector component. Allowing for both, and separating into real and imaginary parts we have

This isn’t anything close to the solution that is expected if we were to start with the scalar Lagrangian for the same problem. That Lagrangian is

and the Euler Lagrange equations give us, for a scalar constant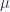

So the solution for is just

In the absence of friction this makes sense. Our angle increases monotonically, and we have circular motion with constant angular velocity. Compare this to the messier 51 derived from the bivector “solution” to the variational problem. There is definitely something wrong with the variational approach (or conclusion) when the variable is a bivector.

Does it help to include the constraints explicitly? The bivector parametrized Lagrangian with the unit bivector multiplier constraint for this system is

Doing the variation we get a set of two equations

Once again re-inserting one gets

Setting , , , we have

This is now consistent with the scalar Lagrangian treatment. In both cases we have the angle linearly proportional to time, and have a single parameter to adjust the angular velocity (used 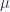in the scalar treatment above and have 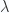this time (although it was set to one here for convenience). The conclusion has to be that the requirement to include the multipliers for the constraints is absolutely necessary to get the right physics out of this bivector parametrized Lagrangian. The good news is that we can get the right physics out of a non-scalar treatment. What is a bit disturbing is that it was fairly difficult in the end to get from the results of the variation to a solution, and that this will not likely get any easier with a more complex system.

A second example.

The scalar expansion 82 of the kinetic term in our spherical polar Lagrangian shows a couple of other specific multivector functions we can consider the variation of.

We have considered an specific example of a Lagrangian function without (yet) utilizing or deriving a multivector form of the Euler-Lagrange equations. Let’s consider a few more specific simple examples motivated by the expansion of the kinetic energy in 82. Lets start with

where is a bivector constant, 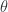a scalar, and 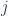a bivector variable for the system. Expanding this around stationary points , and we have to first order

In this simple system where both scalar variable 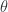and bivector variable 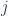are cyclic “coordinates”, we have solutions to the variational problem given by the pair of equations

As to what, if anything, this particular Lagrangian (a fragment picked out of a real Kinetic energy function) represents physically that doesn’t matter so much, since the point of this example was to build up to treating the more general case where we are representing something physical.

A third example.

If we throw a small additional wrench into the problem above and allow to be one of the variables our system is dependent on.

It is less obvious how to do a first order Taylor expansion of this Lagrangian required for the variation around the stationary solution. If all the coordinates in the Lagrangian were scalars as in

(dropping dot products now that these are all scalar variables), then the variation requires nothing abnormal. Suppose our stationary point has coordinates , with variations that vanish at the extremes of the integral as usual.

With scalar variables our path is clear, and we just form

Here is it implied that all the partials are evaluated at the stationary points . Doing the integration by parts we have

Setting this produces the Euler-Lagrange equations for the system. For our specific Lagrangian this procedure gives

Each time we do the first order expansion we are varying just one of the coordinates. It seems likely that the correct answer for the multivariable case will be

Thus the variational problem produces solutions (the coupled equations we still have to solve) of

Multivector Euler-Lagrange equations.

Derivation.

Having considered a few specific Lagrangians dependent on multivector generalized “coordinates”, some basic comfort that it is at least possible has been gained. Let’s now move on to the general case. It is sufficient to consider Lagrangian functions that only depend on blades, since we can write any more general multivector as a sum of such blades

Write

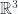where is a blade of grade . We can do a regular old chain rule expansion of this Lagrangian if coordinates are (temporarily) introduced for each of the blades . For example, if is a bivector in , we can write

and then we can do a first order Taylor series expansion of in terms of these coordinates. With , for this specific single variable Lagrangian we have

If we write the coordinate expansion of our blades as

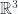where is some set of indexes like from the bivector example, then our chain rule expansion of the Lagrangian to first order about a stationary point becomes

Trying to write this beastie down with abstract indexing variables is a bit ugly. There’s something to be said for not trying to be general since writing this for the single variable bivector example was much clearer. However, having written down the ugly beastie, it can now be cleaned up nicely by introducing position and velocity gradient operators for each of the grades

Utilizing this (assumed) orthonormal basis pair we have

Setting we have a set of equations for each of the blade variables, and the Euler-Lagrange equations take the form

Work some examples.

For the pendulum problem we are really only interested in applying 73 for scalar and bivector variables. Let’s revisit some of the example Lagrangians, functions of bivectors, already considered and see how we can evaluate the position and velocity gradients. This generalized Euler-Lagrange formulation doesn’t do much good if we can’t work with it.

Let’s take the bivector gradient of a couple bivector functions (all the ones considered previously leading up to the multivector Euler-Lagrange equations).

It is actually sufficient (in a less than 4D space) to consider only the first,

For we then have

This is now enough to evaluate our bivector parameterized Lagrangian from the first example, 56, reproducing the result obtained by direct variation (as in Feynman’s lectures)

By inspection we can see that this works for the remaining two motivational examples too.

Evaluating the pendulum Euler-Lagrange equations (scalar, bivector parameterized KE).

We now have the tools to evaluate the Euler-Lagrange equations for the pendulum problem 37. Since all the and dependence is in the kinetic energy we can start with that. For

We want each of and . Of these the derivative is easier, so lets start with that

Each of these are scalars and thus equal their Hermitian conjuagate. This leaves us with just one term doubled

A final evaluation of the derivatives, in block matrix form over rows , gives us

For the bivector velocity gradients, we can do the same,

Only the parts of contribute to the velocity gradients, so we need to know how to evaluate a bivector gradient (as opposed to the square which was done earlier). Expanding in coordinates

(three here because we are in 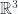, and our bivectors have three independent coordinates).

These terms are both one-by-one bivector matrixes, and negate with Hermitian conjugation, so we can again double up and eliminate one of the two terms, producing

Completing the Euler-Lagrange equation evaluation we have for the coordinates

plus one equation for each of the bivectors

Because the bivector does not (nessessarily) commute with bivectors that are part of there doesn’t look like there’s much hope of assembling the left hand gradients into a nice non-coordinate form. Additionally, looking back at this approach, and the troubles with producing meaningful equations of motion even in the constrained single pendulum case, it appears that a bivector parameterization of the kinetic energy is genally not a good approach. This is an unfortunate conclusion after going through all the effort to develop intuition that led to the multivector Euler-Lagrange formulation for this problem.

Oh well.

The Hermitian formulation used here should still provide a nice compact way of expressing the kinetic energy, even if we work with plain old scalar spherical polar angles 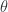, and . Will try this another day, since adding that to these notes will only make them that much more intractable.

Appendix calculation. A verification that the Kinetic matrix product is a real scalar.

In the kinetic term of the rather scary looking Lagrangian of 37 we have what should be a real scalar, but it is not obvious that this is the case. As a validation that nothing very bad went wrong, it seems worthwhile to do a check that this is in fact the case, expanding this out explicitly in gory detail.

One way to try this expansion is utilizing a block matrix summing over the diagonal and paired skew terms separately. That is

Examining the diagonal matrix products and expanding one of these (dropping the suffix for tidiness), we have

Since we are working in 3D this symmetric sum is twice the dot product of the bivector 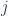with its derivative, which means that it is a scalar. We expect this to be zero though, and can observe that this is the case since 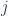was by definition a unit bivector

(thus 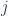and its derivative represent orthogonal oriented planes rather like 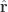and its derivative are orthogonal on a circle or sphere). The implication is that the diagonal subset of the kinetic energy expansion contains just

If we are going to have any complex interaction terms then they will have to come from the off diagonal products. Expanding the first of these

Adding to this the exchanged product and rearranging yields

Each of these multivector sums within the brackets is of the form , a multivector plus its reverse. There can therefore be no bivector or trivector terms since they negate on reversal, and the resulting sum can have only scalar and vector grades. Of these the second term, so it is unarguably a scalar as expected, but additional arguments are required to show this of the other three terms. Of these remaining three, the last two have the same form. Examining the first of these two

The first term actually expands in a similarly straightforward way. The vector terms all cancel, and one is left with just

Writing and (for compactness to fit things all in since the expanded result is messy), all of this KE terms can be assembled into the following explicit scalar expansion

Noting that all the bivector, bivector dot products are scalars really completes the desired verification. We can however, be more explicit using , which gives after a bit of manipulation

These can then be inserted back into 82 in a straightforward fashion, but it is not any more illuminating to do so.

spherical polar line element (continued).

[Click here for a PDF of this sequence of posts with nicer formatting]

REPOSTING WITH ADDITIONAL NOTES.

Line element.

The line element for the particle moving on a spherical surface can be calculated by calculating the derivative of the spherical polar unit vector

than taking the magnitude of this vector. We can start either in coordinate form

or, instead do it the fun way, first grouping this into a complex exponential form. This factorization was done above, but starting over allows this to be done a bit more effectively for this particular problem. As above, writing , the first factorization is

The unit vector lies in the plane perpendicular to , so we can form the unit bivector and further factor the unit vector terms into a form

This allows the spherical polar unit vector to be expressed in complex exponential form (really a vector-quaternion product)

Now, calculating the unit vector velocity, we get

The last two lines above factor the vector and the quaternion to the left and to the right in preparation for squaring this to calculate the magnitude.

This last term () has only grade two components, so the scalar part is zero. We are left with the line element

In retrospect, at least once one sees the answer, it seems obvious. Keeping constant the length increment moving in the plane is , and keeping constant, we have . Since these are perpendicular directions we can add the lengths using the Pythagorean theorem.

Line element using an angle and unit bivector parameterization.

Parameterizing using scalar angles is not the only approach that we can take to calculate the line element on the unit sphere. Proceding directly with a alternate polar representation, utilizing a unit bivector , and scalar angle is

For this product to be a vector must contain as a factor ( for some vector m.) Setting for now, the deriviate of is

This is

Alternately, we can take derivatives of , for

Or

Together with 23, the line element for position change on the unit sphere is then

Starting with cyclic reordering of the last term, we get zero

The line element (for constant ) is therefore

This is essentially the same result as we got starting with an explicit . Repeating for comparision that was

The bivector that we have used this time encodes the orientation of the plane of rotation from the polar axis down to the position on the sphere corresponds to the angle in the
scalar parameterization. The negation in sign is expected due to the negative bivector square.

Also comparing to previous results it is notable that we can explicitly express this bivector in terms of the scalar angle if desired as

The inverse mapping, expressing the scalar angle using the bivector representation is also possible, but not unique. The principle angle for that inverse mapping is

Allowing the magnitude to vary.

Writing a vector in polar form

and also allowing to vary, we have

The squared unit vector derivative was previously calculated to be

Picturing the geometry is enough to know that since is always tangential to the sphere. It should also be possible to algebraically show this, but without going through the effort we at least now know the general line element

Line element for Spherical Polar unit vectors using Geometric Algebra.

[Click here for a PDF incorporating this post with nicer formatting]

The line element for the particle moving on a spherical surface can be calculated by calculating the derivative of the spherical polar unit vector

than taking the magnitude of this vector. We can start either in coordinate form

or, instead do it the fun way, first grouping this into a complex exponential form. Writing , the first factorization is

The unit vector lies in the plane perpendicular to , so we can form the unit bivector and further factor the unit vector terms into a form

This allows the spherical polar unit vector to be expressed in complex exponential form (really a vector-quaternion product)

Now, calcuating the unit vector velocity, we get

The last two lines above factor the vector and the quaternion to the left and to the right in preparation for squaring this to calculate the magnitude.

This last term () has only grade two components, so the scalar part is zero. We are left with the line element

In retrospect, at least once one sees the answer, it seems obvious. Keeping constant the length increment moving in the plane is , and keeping constant, we have . Since these are perpendicular directions we can add the lengths using the Pythagorean theorem.

Spherical Polar unit vectors in exponential form.

[Click here for a PDF of this post with nicer formatting]

Motivation

In [1] I blundered on a particularly concise exponential non-coordinate form for the unit vectors in a spherical polar coordinate system. For future reference outside of a quantum mechanical context here is a separate and more concise iteration of these results.

The rotation and notation.

The spherical polar rotor is a composition of rotations, expressed as half angle exponentials. Following the normal physics conventions we first apply a plane rotation by angle theta, then an plane rotation by angle . This produces the rotor

Our triplet of Cartesian unit vectors is therefore rotated as

In the quantum mechanical context it was convenient to denote the plane unit bivector with the imaginary symbol

reserving for the spatial pseudoscalar the capital

Note the characteristic differences between these two “imaginaries”. The planar quantity commutes with , but anticommutes with either or . On the other hand the spatial pseudoscalar commutes with any vector, bivector or trivector in the algebra.

Application of the rotor. The spherical polar unit vectors.

Having fixed notation, lets apply the rotation to each of the unit vectors in sequence, starting with the calculation for . This is

Here, since commutes with the rotor bivector the innermost exponentials cancel, leaving just the rotation. For it is a bit messier, and we have

Finally for , we have a similar messy expansion

Summarizing the three of these relations we have for the rotated unit vectors

and in particular for the radial position vector from the origin, rotating from the polar axis, we have

Compare this to the coordinate representation

it is not initially obvious that these and rotations admit such a tidy factorization.

A small example application.

Let’s use these results to compute the spherical polar volume element. Pictorially this can be read off simply from a diagram. If one is less trusting of pictorial means (or want a method more generally applicable), we can also do this particular calculation algebraically, expanding the determinant of partials

One can chug through the trig reduction for this determinant with not too much trouble, but it isn’t particularly fun.

Now compare to the same calculation proceeding directly with the exponential form. We do still need to compute the partials

So the area element, the oriented area of the parallelogram between the two vectors , and on the spherical surface at radius is

and the volume element in trivector form is just the product

References

[1] Peeter Joot. Bivector form of quantum angular momentum operator [online]. http://sites.google.com/site/peeterjoot/math2009/qmAngularMom.pdf.

A summary: Bivector form of quantum angular momentum operator

[Click here for a PDF of this sequence of posts with nicer formatting]

Having covered a fairly wide range in the previous Geometric Algebra exploration of the angular momentum operator, it seems worthwhile to attempt to summarize what was learned.

The exploration started with a simple observation that the use of the spatial pseudoscalar for the imaginary of the angular momentum operator in its coordinate form

allowed for expressing the angular momentum operator in its entirety as a bivector valued operator

The bivector representation has an intrinsic complex behavior, eliminating the requirement for an explicitly imaginary as is the case in the coordinate representation.

It was then assumed that the Laplacian can be expressed directly in terms of . This isn’t an unreasonable thought since we can factor the gradient with components projected onto and perpendicular to a constant reference vector as

and this squares to a Laplacian expressed in terms of these constant reference directions

a quantity that has an angular momentum like operator with respect to a constant direction. It was then assumed that we could find an operator representation of the form

Where was to be determined, and was found by subtraction. Thinking ahead to relativistic applications this result was obtained for the n-dimensional Laplacian and was found to be

For the 3D case specifically this is

While the scalar selection above is good for some purposes, it interferes with observations about simultaneous eigenfunctions for the angular momentum operator and the scalar part of its square as seen in the Laplacian. With some difficulty and tedium, by subtracting the bivector and quadvector grades from the squared angular momentum operator it was eventually found that (76) can be written as

In the 3D case the quadvector vanishes and (77) with the scalar selection removed is reduced to

In 3D we also have the option of using the duality relation between the cross and the wedge to express the Laplacian

Since it is customary to express angular momentum as , we see here that the imaginary in this context should perhaps necessarily be viewed as the spatial pseudoscalar. It was that guess that led down this path, and we come full circle back to this considering how to factor the Laplacian in vector quantities. Curiously this factorization is in no way specific to Quantum Theory.

A few verifications of the Laplacian in (80) were made. First it was shown that the directional derivative terms containing , are equivalent to the radial terms of the Laplacian in spherical polar coordinates. That is

Employing the quaternion operator for the spherical polar rotation

it was also shown that there was explicitly no radial dependence in the angular momentum operator which takes the form

Because there is a , and dependence in the unit vectors , , and , squaring the angular momentum operator in this form means that the unit vectors are also operated on. Those vectors were given by the triplet

Using for the spatial pseudoscalar, and (a possibly confusing switch of notation) for the bivector of the x-y plane we can write the spherical polar unit vectors in exponential form as

These or related expansions were used to verify (with some difficulty) that the scalar squared bivector operator is identical to the expected scalar spherical polar coordinates parts of the Laplacian

Additionally, by left or right dividing a unit bivector from the angular momentum operator, we are able to find that the raising and lowering operators are left as one of the factors

Both of these use , the bivector for the plane, and not the spatial pseudoscalar. We are then able to see that in the context of the raising and lowering operator for the radial equation the interpretation of the imaginary should be one of a plane.

Using the raising operator factorization, it was calculated that was an eigenfunction of the bivector operator with eigenvalue . This results in the simultaneous eigenvalue of for this eigenfunction with the scalar squared angular momentum operator.

There are a few things here that have not been explored to their logical conclusion.

The bivector Fourier projections do not obey the commutation relations of the scalar angular momentum components, so an attempt to directly use these to construct raising and lowering operators does not produce anything useful. The raising and lowering operators in a form that could be used to find eigensolutions were found by factoring out from the bivector operator. Making this particular factorization was a fluke and only because it was desirable to express the bivector operator entirely in spherical polar form. It is curious that this results in raising and lowering operators for the x,y plane, and understanding this further would be nice.

In the eigen solutions for the bivector operator, no quantization condition was imposed. I don’t understand the argument that Bohm used to do so in the traditional treatment, and revisiting this once that is done is in order.

I am also unsure exactly how Bohm knows that the inner product for the eigenfunctions should be a surface integral. This choice works, but what drives it. Can that be related to anything here?