On conditions for Clebsh-Gordan coefficients to be zero

[Click here for a PDF of this post with nicer formatting and figures if the post had any (especially if my latex to wordpress script has left FORMULA DOES NOT PARSE errors.)]

Motivation.

In section 28.2 of the text [1] is a statement that the Clebsh-Gordan coefficient

unless . It appeared that it was related to the operation of , but how exactly wasn’t obvious to me. In tutorial today we hashed through this. Here’s the details lying behind this statement

Recap on notation.

We are taking an arbitrary two particle ket and decomposing it utilizing an insertion of a complete set of states

with and fixed, this is written with the shorthand

so that we write

The action.

We have two ways that we can apply the operator to . One is using the sum above, for which we find

We can also act directly on and then insert a complete set of states

This provides us with the identity

This equality must be valid for any , and since all the kets are linearly independent, we must have for any

We have two ways to get this zero. One of them is a condition, and the other is for the CG coeff to be zero whenever .

It’s not a difficult argument, but one that wasn’t clear from a read of the text (at least to me).

References

[1] BR Desai. Quantum mechanics with basic field theory. Cambridge University Press, 2009.

PHY456H1F: Quantum Mechanics II. Lecture 18 (Taught by Prof J.E. Sipe). The Clebsch-Gordon convention for the basis elements of summed generalized angular momentum

[Click here for a PDF of this post with nicer formatting and figures if the post had any (especially if my latex to wordpress script has left FORMULA DOES NOT PARSE errors.)]

Disclaimer.

Peeter’s lecture notes from class. May not be entirely coherent.

Recap.

Recall our table

First column

Let’s start with computation of the kets in the lowest position of the first column, which we will obtain by successive application of the lowering operator to the state

Recall that our lowering operator was found to be (or defined as)

so that application of the lowering operator gives us

Proceeding iteratively would allow us to finish off this column.

Second column

Moving on to the second column, the top most element in the table

can only be made up of with . There are two possibilities

So for some and to be determined we must have

Observe that these are the same kets that we ended up with by application of the lowering operator on the topmost element of the first column in our table. Since and are orthogonal, we can construct our ket for the top of the second column by just seeking such an orthonormal superposition. Consider for example

With we find that , so we have

So we find, for real and that

for any orthonormal pair of kets and . Using this we find

This will work, although we could also multiply by any phase factor if desired. Such a choice of phase factors is essentially just a convention.

The Clebsch-Gordon convention

This is the convention we will use, where we

\begin{itemize}
\item choose the coefficients to be real.
\item require the coefficient of the term to be
\end{itemize}

This gives us the first state in the second column, and we can proceed to iterate using the lowering operators to get all those values.

Moving on to the third column

can only be made up of with . There are now three possibilities

and 2 orthogonality conditions, plus conventions. This is enough to determine the ket in the third column.

We can formally write

where

and

are the Clebsch-Gordon coefficients, sometimes written as

Properties
\begin{enumerate}
\item only if

This is sometimes called the triangle inequality, depicted in figure (\ref{fig:qmTwoL18:qmTwoL18fig1})

\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{qmTwoL18fig1}
\caption{Angular momentum triangle inequality.}
\end{figure}

\item only if .

\item Real (convention).

\item positive (convention again).

\item Proved in the text. If follows that

\end{enumerate}

Note that the are all real. So, they can be assembled into an orthogonal matrix. Example

Example. Electrons

Consider the special case of an electron, a spin particle with and where we have

possible values of are

Our table representation is then

Here

can only have contributions from

from the same two. So using this and conventions we can work out (in section 28 page 524, of our text [1]).

Tensor operators

section 29 of the text.

Recall how we characterized a rotation

Here we are using an active rotation as depicted in figure (\ref{fig:qmTwoL18:qmTwoL18fig2})

\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{qmTwoL18fig2}
\caption{active rotation}
\end{figure}

Suppose that

so that

rotates in the same way. Rotating a ket as in figure (\ref{fig:qmTwoL18:qmTwoL18fig3})
\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{qmTwoL18fig3}
\caption{Rotating a wavefunction.}
\end{figure}

Rotating a ket

using the prescription

and write

Now look at

and compare with

We’ll be looking in more detail at .

References

[1] BR Desai. Quantum mechanics with basic field theory. Cambridge University Press, 2009.

PHY456H1F: Quantum Mechanics II. Lecture 16 (Taught by Prof J.E. Sipe). Hydrogen atom with spin, and two spin systems.

[Click here for a PDF of this post with nicer formatting and figures if the post had any (especially if my latex to wordpress script has left FORMULA DOES NOT PARSE errors.)]

Disclaimer.

Peeter’s lecture notes from class. May not be entirely coherent.

The hydrogen atom with spin.

READING: what chapter of [1] ?

For a spinless hydrogen atom, the Hamiltonian was

where we have independent Hamiltonian’s for the motion of the center of mass and the relative motion of the electron to the proton.

The basis kets for these could be designated and respectively.

Now we want to augment this, treating

where is the Hamiltonian for the spin of the electron. We are neglecting the spin of the proton, but that could also be included (this turns out to be a lesser effect).

We’ll introduce a Hamiltonian including the dynamics of the relative motion and the electron spin

Covering the Hilbert space for this system we’ll use basis kets

Here should be understood to really mean . Our full Hamiltonian, after introducing a magnetic pertubation is

where

and

For a uniform magnetic field

We also have higher order terms (higher order multipoles) and relativistic corrections (like spin orbit coupling [2]).

Two spins.

READING: section 28 of [1].

Example: Consider two electrons, 1 in each of 2 quantum dots.

where and are both spin Hamiltonian’s for respective 2D Hilbert spaces. Our complete Hilbert space is thus a 4D space.

We’ll write

Can introduce

Here we “promote” each of the individual spin operators to spin operators in the complete Hilbert space.

We write

Write

for the full spin angular momentum operator. The component of this operator is

So, we find that are all eigenkets of . These will also all be eigenkets of since we have

Are all the product kets also eigenkets of ? Calculate

For the mixed terms, we have

So

Since we have set our spin direction in the z direction with

We have

And are able to arrive at the action of on our mixed composite state

For the action on the state we have

and on the state we have

All of this can be assembled into a tidier matrix form

where the matrix is taken with respect to the (ordered) basis

However,

It should be possible to find eigenkets of and

An orthonormal set of eigenkets of and is found to be

latex s = 1$ and } \\ \frac{1}{{\sqrt{2}}} \left( {\left\lvert {+-} \right\rangle} + {\left\lvert {-+} \right\rangle} \right) & \mbox{ and } \\ {\left\lvert {–} \right\rangle} & \mbox{ and } \\ \frac{1}{{\sqrt{2}}} \left( {\left\lvert {+-} \right\rangle} – {\left\lvert {-+} \right\rangle} \right) & \mbox{ and }\end{array}\end{aligned} \hspace{\stretch{1}}(3.37)$

The first three kets here can be grouped into a triplet in a 3D Hilbert space, whereas the last treated as a singlet in a 1D Hilbert space.

Form a grouping

Can write

where the and here refer to the spin index .

Other examples

Consider, perhaps, the state of the hydrogen atom

Consider the Hilbert space spanned by , a dimensional space. How to find the eigenkets of and ?

References

[1] BR Desai. Quantum mechanics with basic field theory. Cambridge University Press, 2009.

[2] Wikipedia. Spin.orbit interaction — wikipedia, the free encyclopedia [online]. 2011. [Online; accessed 2-November-2011]. http://en.wikipedia.org/w/index.php?title=Spin\%E2\%80\%93orbit_interaction&oldid=451606718.

PHY456H1F: Quantum Mechanics II. Lecture 15 (Taught by Prof J.E. Sipe). Rotation operator in spin space

[Click here for a PDF of this post with nicer formatting and figures if the post had any (especially if my latex to wordpress script has left FORMULA DOES NOT PARSE errors.)]

Disclaimer.

Peeter’s lecture notes from class. May not be entirely coherent.

Rotation operator in spin space.

We can formally expand our rotation operator in Taylor series

or

where we’ve used the fact that .

So our representation of the spin operator is

Note that, in particular,

This “rotates” the ket, but introduces a phase factor.

Can do this in general for other degrees of spin, for .

Unfortunate interjection by me

I mentioned the half angle rotation operator that requires a half angle operator sandwich. Prof. Sipe thought I might be talking about a Heisenberg picture representation, where we have something like this in expectation values

so that

However, what I was referring to, was that a general rotation of a vector in a Pauli matrix basis

can be expressed by sandwiching the Pauli vector representation by two half angle rotation operators like our spin 1/2 operators from class today

where and are two non-colinear orthogonal unit vectors that define the oriented plane that we are rotating in.

For example, rotating in the plane, with and , we have

Observe that these exponentials commute with , leaving

yielding our usual coordinate rotation matrix. Expressed in terms of a unit normal to that plane, we form the normal by multiplication with the unit spatial volume element . For example:

and can in general write a spatial rotation in a Pauli basis representation as a sandwich of half angle rotation matrix exponentials

when we get the complex-number like single sided exponential rotation exponentials (since commutes with in that case)

I believe it was pointed out in one of [1] or [2] that rotations expressed in terms of half angle Pauli matrices has caused some confusion to students of quantum mechanics, because this “rotation” only generates half of the full spatial rotation. It was argued that this sort of confusion can be avoided if one observes that these half angle rotations exponentials are exactly what we require for general spatial rotations, and that a pair of half angle operators are required to produce a full spatial rotation.

The book [1] takes this a lot further, and produces a formulation of spin operators that is devoid of the normal scalar imaginary (using the Clifford algebra spatial unit volume element instead), and also does not assume a specific matrix representation of the spin operators. They argue that this leads to some subtleties associated with interpretation, but at the time I was attempting to read that text I did know enough QM to appreciate what they were doing, and haven’t had time to attempt a new study of that content.

Spin dynamics

At least classically, the angular momentum of charged objects is associated with a magnetic moment as illustrated in figure (\ref{fig:qmTwoL15:qmTwoL15fig1})

\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{qmTwoL15fig1}
\caption{Magnetic moment due to steady state current}
\end{figure}

In our scheme, following the (cgs?) text conventions of [3], where the and have the same units, we write

For a charge moving in a circle as in figure (\ref{fig:qmTwoL15:qmTwoL15fig2})
\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{qmTwoL15fig2}
\caption{Charge moving in circle.}
\end{figure}

so the magnetic moment is

Here is the gyromagnetic ratio

Recall that we have a torque, as shown in figure (\ref{fig:qmTwoL15:qmTwoL15fig3})
\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{qmTwoL15fig3}
\caption{Induced torque in the presence of a magnetic field.}
\end{figure}

tending to line up with . The energy is then

Also recall that this torque leads to precession as shown in figure (\ref{fig:qmTwoL15:qmTwoL15fig4})

\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{qmTwoL15fig4}
\caption{Precession due to torque.}
\end{figure}

with precession frequency

For a current due to a moving electron

where we are, here, writing for charge on the electron .

Question: steady state currents only?. Yes, this is only true for steady state currents.

For the translational motion of an electron, even if it is not moving in a steady way, regardless of it’s dynamics

Now, back to quantum mechanics, we turn into a dipole moment operator and is “promoted” to an angular momentum operator.

What about the “spin”?

Perhaps

we write this as

so that

Experimentally, one finds to very good approximation

There was a lot of trouble with this in early quantum mechanics where people got things wrong, and canceled the wrong factors of .

In fact, Dirac’s relativistic theory for the electron predicts .

When this is measured experimentally, one does not get exactly , and a theory that also incorporates photon creation and destruction and the interaction with the electron with such (virtual) photons. We get

Richard Feynman compared the precision of quantum mechanics, referring to this measurement, “to predicting a distance as great as the width of North America to an accuracy of one human hair’s breadth”.

References

[1] C. Doran and A.N. Lasenby. Geometric algebra for physicists. Cambridge University Press New York, Cambridge, UK, 1st edition, 2003.

[2] D. Hestenes. New Foundations for Classical Mechanics. Kluwer Academic Publishers, 1999.

[3] BR Desai. Quantum mechanics with basic field theory. Cambridge University Press, 2009.

PHY456H1F: Quantum Mechanics II. Lecture 14 (Taught by Prof J.E. Sipe). Representation of two state kets and Pauli spin matrices.

[Click here for a PDF of this post with nicer formatting and figures if the post had any (especially if my latex to wordpress script has left FORMULA DOES NOT PARSE errors.)]

Disclaimer.

Peeter’s lecture notes from class. May not be entirely coherent.

Representation of kets.

Reading: section 5.1 – section 5.9 and section 26 in [1].

We found the representations of the spin operators

How about kets? For example for

and

So, for example

Kets in

This is a “spinor”

Put

with

Use

So

Alternatively

In braces we have a ket in , let’s call it

then

where the direct product is implied.

We can form a ket in as

An operator which acts on alone can be promoted to , which is now an operator that acts on . We are sometimes a little cavalier in notation and leave this off, but we should remember this.

and likewise

and

Suppose we want to rotate a ket, we do this with a full angular momentum operator

(recalling that and commute)

So

A simple example.

Suppose

where

Then

where

for

so

We are going to concentrate on the unentagled state of 2.26.

\begin{itemize}
\item
How about with

is an eigenket of with eigenvalue .
\item

is an eigenket of with eigenvalue .

\item
What is if it is an eigenket of ?
\end{itemize}

FIXME: F1: standard spherical projection picture, with projected down onto the plane at angle and at an angle from the axis.

The eigenvalues will still be since there is nothing special about the direction.

To find the eigenkets we diagonalize this, and we find representations of the eigenkets are

with eigenvalues and respectively.

So in the abstract notation, tossing the specific representation, we have

Representation of two state kets

Every ket

for which

can be written in the form 2.34 for some and , neglecting an overall phase factor.

For any ket in , that ket is “spin up” in some direction.

FIXME: show this.

Pauli spin matrices.

It is useful to write

where

These are the Pauli spin matrices.

Interesting properties.

\begin{itemize}
\item

latex i < j$}\end{aligned} \hspace{\stretch{1}}(4.46)$

\item

(and cyclic permutations)

\item

\item

where

and

(note )

\item

(and cyclic permutations of the latter).

Can combine these to show that

where and are vectors (or more generally operators that commute with the matrices).

\item

\item

where
\end{itemize}

Note that any complext matrix can be written as

for any four complex numbers

where

References

[1] BR Desai. Quantum mechanics with basic field theory. Cambridge University Press, 2009.

PHY456H1F: Quantum Mechanics II. Lecture 11 (Taught by Prof J.E. Sipe). Spin and Spinors

[Click here for a PDF of this post with nicer formatting and figures if the post had any (especially if my latex to wordpress script has left FORMULA DOES NOT PARSE errors.)]

Disclaimer.

Peeter’s lecture notes from class. May not be entirely coherent.

Generators.

Covered in section 26 of the text [1].

Example: Time translation

The Hamiltonian “generates” evolution (or translation) in time.

Example: Spatial translation

\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{qmTwoL11fig1}
\caption{Vector translation.}

\end{figure}

is the operator that generates translations. Written out, we have

where the factorization was possible because , , and commute

for any (including as I dumbly questioned in class … this is a commutator, so ).

The fact that the commute means that successive translations can be done in any orderr and have the same result.

In class we were rewarded with a graphic demo of translation component commutation as Professor Sipe pulled a giant wood carving of a cat (or tiger?) out from beside the desk and proceeded to translate it around on the desk in two different orders, with the cat ending up in the same place each time.

Exponential commutation.

Note that in general

unless . To show this one can compare

and

Comparing the second order (for example) we see that we must have for equality

or

or

Translating a ket

If we consider the quantity

does this ket “translated” by make any sense? The vector lives in a 3D space and our ket lives in Hilbert space. A quantity like this deserves some careful thought and is the subject of some such thought in the Interpretations of Quantum mechanics course. For now, we can think of the operator and ket as a “gadget” that prepares a state.

A student in class pointed out that can be dependent on many degress of freedom, for example, the positions of eight different particles. This translation gadget in such a case acts on the whole kit and kaboodle.

Now consider the matrix element

Note that

so

or

This is what we expect of a translated function, as illustrated in figure (\ref{fig:qmTwoL11:qmTwoL11fig2})
\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{qmTwoL11fig2}
\caption{Active spatial translation.}
\end{figure}

Example: Spatial rotation

We’ve been introduced to the angular momentum operator

where

We also found that

These non-zero commutators show that the components of angular momentum do not commute.

Define

This is the vecvtor that we get by actively rotating the vector by an angule counterclockwise about , as in figure (\ref{fig:qmTwoL11:qmTwoL11fig3})

\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{qmTwoL11fig3}
\caption{Active vector rotations}
\end{figure}

An active rotation rotates the vector, leaving the coordinate system fixed, whereas a passive rotation is one for which the coordinate system is rotated, and the vector is left fixed.

Note that rotations do not commute. Suppose that we have a pair of rotations as in figure (\ref{fig:qmTwoL11:qmTwoL11fig4})
\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{qmTwoL11fig4}
\caption{A example pair of non-commuting rotations.}
\end{figure}

Again, we get the graphic demo, with Professor Sipe rotating the big wooden cat sculpture. Did he bring that in to class just to make this point (too bad I missed the first couple minutes of the lecture).

Rather amusingly, he points out that most things in life do not commute. We get much different results if we apply the operations of putting water into the teapot and turning on the stove in different orders.

Rotating a ket

With a rotation gadget

we can form the matrix element

In this we have

so

or

Generalizations.

Recall what you did last year, where , , and were defined mechaniccally. We found

\begin{itemize}
\item generates time evolution (or translation in time).
\item generates spatial translation.
\item generates spatial rotation.
\end{itemize}

For our mechanical definitions we have

and

These are the relations that show us the way translations and rotations combine. We want to move up to a higher plane, a new level of abstraction. To do so we define as the operator that generates time evolution. If we have a theory that covers the behaviour of how anything evolves in time, encodes the rules for this time evolution.

Define as the operator that generates translations in space.

Define as the operator that generates rotations in space.

In order that these match expectations, we require

and

In the simple theory of a spinless particle we have

We actually need a generalization of this since this is, in fact, not good enought, even for low energy physics.

Many component wave functions.

We are free to construct tuples of spatial vector functions like

or

etc.

We will see that these behave qualitatively different than one component wave functions. We also don’t have to be considering multiple particle wave functions, but just one particle that requires three functions in to describe it (ie: we are moving in on spin).

Question: Do these live in the same vector space?
Answer: We will get to this.

A classical analogy.

“There’s only bad analogies, since if the are good they’d be describing the same thing. We can however, produce some useful bad analogies”

\begin{enumerate}
\item A temperature field

\item Electric field

\end{enumerate}

These behave in a much different way. If we rotate a scalar field like as in figure (\ref{fig:qmTwoL11:qmTwoL11fig5})
\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{qmTwoL11fig5}
\caption{Rotated temperature (scalar) field}
\end{figure}

Suppose we have a temperature field generated by, say, a match. Rotating the match above, we have

Compare this to the rotation of an electric field, perhaps one produced by a capacitor, as in figure (\ref{fig:qmTwoL11:qmTwoL11fig6})

\begin{figure}[htp]
\centering
\includegraphics[totalheight=0.2\textheight]{qmTwoL11fig6}
\caption{Rotating a capacitance electric field}
\end{figure}

Is it true that we have

No. Because the components get mixed as well as the positions at which those components are evaluated.

We will work with many component wave functions, some of which will behave like vectors, and will have to develope the methods and language to tackle this.

References

[1] BR Desai. Quantum mechanics with basic field theory. Cambridge University Press, 2009.

PHY456H1F, Quantum Mechanics II. My solutions to problem set 1 (ungraded).

[Click here for a PDF of this post with nicer formatting (especially if my latex to wordpress script has left FORMULA DOES NOT PARSE errors.)]

Harmonic oscillator.

Consider

Since it’s been a while let’s compute the raising and lowering factorization that was used so extensively for this problem.

It was of the form

Why this factorization has an imaginary in it is a good question. It’s not one that is given any sort of rationale in the text ([1]).

It’s clear that we want and . The difference is then

That commutator is an value, but what was the sign? Let’s compute so we don’t get it wrong

So we have

Factoring out an produces the form of the Hamiltonian that we used before

The factors were labeled the uppering () and lowering () operators respectively, and written

Observe that we can find the inverse relations

Question
What is a good reason that we chose this particular factorization? For example, a quick computation shows that we could have also picked

I don’t know that answer. That said, this second factorization is useful in that it provides the commutator relation between the raising and lowering operators, since subtracting 1.11 and 1.6 yields

If we suppose that we have eigenstates for the operator of the form

then the problem of finding the eigensolution of reduces to solving this problem. Because commutes with , an eigenstate of is also an eigenstate of . Utilizing 1.12 we then have

so we see that is an eigenstate of with eigenvalue .

Similarly for the raising operator

and find that is also an eigenstate of with eigenvalue .

Supposing that there is a lowest energy level (because the potential has a lower bound of zero) then the state for which the energy is the lowest when operated on by we have

Thus

and

This seems like a small bit of slight of hand, since it sneakily supplies an integer value to where up to this point was just a label.

If the eigenvalue equation we are trying to solve for the Hamiltonian is

Then we must then have

Part (a)

We’ve now got enough context to attempt the first part of the question, calculation of

We’ve calculated things like this before, such as

To continue we need an exact relation between and . Recall that was an eigenstate of with eigenvalue . This implies that the eigenstates and are proportional

or

so that

Similarly let

or

so that

We can now return to 1.19, and find

Consider half of this braket

Squaring, utilizing the Hermitian nature of the operator

Part (b)

Find the ground state energy of the Hamiltonian for .

The new Hamiltonian has the form

where

The energy states of the Hamiltonian are thus

and the ground state of the modified Hamiltonian is thus

Part (c)

Find the ground state energy of the Hamiltonian .

With a bit of play, this new Hamiltonian can be factored into

where

From 1.29 we see that we have the same sort of commutator relationship as in the original Hamiltonian

and because of this, all the preceding arguments follow unchanged with the exception that the energy eigenstates of this Hamiltonian are shifted by a constant

where the states are simultaneous eigenstates of the operator

The ground state energy is then

This makes sense. A translation of the entire position of the system should not effect the energy level distribution of the system, but we have set our reference potential differently, and have this constant energy adjustment to the entire system.

Hydrogen atom and spherical harmonics.

We are asked to show that for any eigenkets of the hydrogen atom we have

The summary sheet provides us with the wavefunction

where is a real valued function defined in terms of Lagueere polynomials. Working with the expectation of the operator to start with we have

Recalling that the only dependence in is we can perform the integration directly, which is

We have the same story for the expectation which is

Our integral is then just

also zero. The expectation is a slightly different story. There we have

Within this last integral we can make the substitution

and the integral takes the form

Here we have the product of two even functions, times one odd function (), over a symmetric interval, so the end result is zero, completing the problem.

I wasn’t able to see how to exploit the parity result suggested in the problem, but it wasn’t so bad to show these directly.

Angular momentum operator.

Working with the appropriate expressions in Cartesian components, confirm that for each component of angular momentum , if is in fact only a function of .

In order to proceed, we will have to consider a matrix element, so that we can operate on in position space. For that matrix element, we can proceed to insert complete states, and reduce the problem to a question of wavefunctions. That is

With we have

We are left with an sum of a symmetric product with the antisymmetric tensor so this is zero for all .

References

[1] BR Desai. Quantum mechanics with basic field theory. Cambridge University Press, 2009.

A problem on spherical harmonics.

[Click here for a PDF of this post with nicer formatting]

Motivation.

One of the PHY356 exam questions from the final I recall screwing up on, and figuring it out after the fact on the drive home. The question actually clarified a difficulty I’d had, but unfortunately I hadn’t had the good luck to perform such a question, to help figure this out before the exam.

From what I recall the question provided an initial state, with some degeneracy in , perhaps of the following form

and a Hamiltonian of the form

From what I recall of the problem, I am going to reattempt it here now.

Evolved state.

One part of the question was to calculate the evolved state. Application of the time evolution operator gives us

Now we note that , and , so the exponentials reduce this nicely to just

Probabilities for measurement outcomes.

I believe we were also asked what the probabilities for the outcomes of a measurement of at this time would be. Here is one place that I think that I messed up, and it is really a translation error, attempting to get from the english description of the problem to the math description of the same. I’d had trouble with this process a few times in the problems, and managed to blunder through use of language like “measure”, and “outcome”, but don’t think I really understood how these were used properly.

What are the outcomes that we measure? We measure operators, but the result of a measurement is the eigenvalue associated with the operator. What are the eigenvalues of the operator? These are the values, from the operation . So, given this initial state, there are really two outcomes that are possible, since we have two distinct eigenvalues. These are and for , and respectively.

A measurement of the “outcome” , will be the probability associated with the amplitude (ie: the absolute square of this value). That is

Now, the only other outcome for a measurement of for this state is a measurement of , and the probability of this is then just . On the exam, I think I listed probabilities for three outcomes, with values respectively, but in retrospect that seems blatently wrong.

Probabilities for measurement outcomes.

What are the probabilities for the outcomes for a measurement of after this? The first question is really what are the outcomes. That’s really a question of what are the possible eigenvalues of that can be measured at this point. Recall that we have

So for a state that has only contributions before the measurement, the eigenvalues that can be observed for the operator are respectively and respectively.

For the case, our probability is , leaving as the probability for measurement of the () eigenvalue. We can compute this two ways, and it seems worthwhile to consider both. This first method makes use of the fact that the operator leaves the state vector intact, but it also seems like a bit of a cheat. Consider instead two possible results of measurement after the observation. When an measurement of is performed our state will be left with only the kets. That is

whereas, when a measurement of is performed our state would then only have the contribution, and would be

We have two possible ways of measuring the eigenvalue for . One is when our state was (, and the resulting state has a component, and the other is after the measurement, where our state is left with a component.

The resulting probability is then a conditional probability result

The result is the same, as expected, but this is likely a more convicing argument.

Some worked problems from old PHY356 exams.

[Click here for a PDF of this post with nicer formatting]

Motivation.

Some of the old exam questions that I did for preparation for the exam I liked, and thought I’d write up some of them for potential future reference.

Questions from the Dec 2007 PHY355H1F exam.

1b. Parity operator.

\paragraph{Q:} If is the parity operator, defined by , where is the eigenket of the position operator with eigenvalue ), and is the momentum operator conjugate to , show (carefully) that .

\paragraph{A:}

Consider the matrix element . This is

We’ve taken advantage of the Hermitian property of and here, and can rearrange for

Since this is true for all and we have

Right multiplication by and rearranging we have

1f. Free particle propagator.

\paragraph{Q:} For a free particle moving in one-dimension, the propagator (i.e. the coordinate representation of the evolution operator),

is given by

\paragraph{A:}

This problem is actually fairly straightforward, but it is nice to work it having had a similar problem set question where we were asked about this time evolution operator matrix element (ie: what it’s physical meaning is). Here we have a concrete example of the form of this matrix operator.

Proceeding directly, we have

which is the desired result. Now, let’s look at how this would be used. We can express our time evolved state using this matrix element by introducing an identity

This gives us

However, note that our free particle wave function at time zero is

So the convolution integral 2.6 does not exist. We likely have to require that the solution be not a pure state, but instead a superposition of a set of continuous states (a wave packet in position or momentum space related by Fourier transforms). That is

The time evolution of this wave packet is then determined by the propagator, and is

or in terms of the position space wave packet evaluated at time zero

We see that the propagator also ends up with a Fourier transform structure, and we have

Does that Fourier transform exist? I’d not be surprised if it ended up with a delta function representation. I’ll hold off attempting to evaluate and reduce it until another day.

4. Hydrogen atom.

This problem deals with the hydrogen atom, with an initial ket

where

etc.

\paragraph{Q: (a)}

If no measurement is made until time ,

what is the ket just before the measurement is made?

\paragraph{A:}

Our time evolved state is

Also observe that this initial time was picked to make the exponential values come out nicely, and we have

so our time evolved state is just

\paragraph{Q: (b)}

Suppose that at time an measurement is made, and the outcome 0 is recorded. What is the appropriate ket right after the measurement?

\paragraph{A:}

A measurement with outcome 0, means that the operator measurement found the state at that point to be the eigenstate for eigenvalue 0. Recall that if is an eigenstate of we have

so a measurement of with outcome zero means that we have . Our measurement of at time therefore filters out all but the states and our new state is proportional to the projection over all states as follows

A final normalization yields

\paragraph{Q: (c)}

Right after this measurement, what is ?

\paragraph{A:}

Our amplitude is

so the probability density is

\paragraph{Q: (d)}

If then a position measurement is made immediately, which if any components of the expectation value of will be nonvanishing? Justify your answer.

\paragraph{A:}

The expectation value of this vector valued operator with respect to a radial state can be expressed as

where .

Consider one of the matrix elements, and expand this by introducing an identity twice

Because our state has only contributions, the only dependence for the and components of come from those components themselves. For , we therefore integrate , and for we integrate , and these terms vanish. Our expectation value for for this state, therefore lies completely on the axis.

Questions from the Dec 2008 PHY355H1F exam.

1b. Trace invariance for unitary transformation.

\paragraph{Q:} Show that the trace of an operator is invariant under unitary transforms, i.e. if , where is a unitary operator, prove .

\paragraph{A:}

The bulk of this question is really to show that commutation of operators leaves the trace invariant (unless this is assumed). To show that we start with the definition of the trace

Thus we have

For the unitarily transformed operator we have

1d. Determinant of an exponential operator in terms of trace.

\paragraph{Q:} If is an Hermitian operator, show that

where the Determinant () of an operator is the product of all its eigenvectors.

\paragraph{A:}

The eigenvalues clue in the question provides the starting point. We write the exponential in its series form

Now, suppose that we have the following eigenvalue relationships for

From this the exponential is

We see that the eigenstates of are those of , with eigenvalues .

By the definition of the determinant given we have

1e. Eigenvectors of the Harmonic oscillator creation operator.

\paragraph{Q:} Prove that the only eigenvector of the Harmonic oscillator creation operator is .

\paragraph{A:}

Recall that the creation (raising) operator was given by

where . Now assume that so that

Write , and expand the LHS using 3.27 for

As usual write , and rearrange. This gives us

Observe that this can be viewed as a homogeneous LDE of the form

augmented by a forcing term . The homogeneous equation has the solution , so for the complete equation we assume a solution

Since , we produce a LDE of

or

This has solution , so our solution for 3.29 is

This wave function is an imaginary Gaussian with minimum at . It is also unnormalizable since we require for any 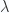if . Since , we must also have , completing the exercise.

2. Two level quantum system.

Consider a two-level quantum system, with basis states . Suppose that the Hamiltonian for this system is given by

where 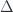and 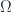are real positive constants.

\paragraph{Q: (a)} Find the energy eigenvalues and the normalized energy eigenvectors (expressed in terms of the basis). Write the time evolution operator using these eigenvectors.

\paragraph{A:}

The eigenvalue part of this problem is probably easier to do in matrix form. Let

Our Hamiltonian is then

Computing , we get

Let . Our normalized eigenvectors are found to be

In terms of and , we then have

Note that our Hamiltonian has a simple form in this basis. That is

Observe that once we do the diagonalization, we have a Hamiltonian that appears to have the form of a scaled projector for an open Stern-Gerlach aparatus.

Observe that the diagonalized Hamiltonian operator makes the time evolution operator’s form also simple, which is, by inspection

Since we are asked for this in terms of , and , the projectors are required. These are

Substitution into 3.42 and a fair amount of algebra leads to

Note that while a big cumbersome, we can also verify that we can recover the original Hamiltonian from 3.41 and 3.43.

\paragraph{Q: (b)}

Suppose that the initial state of the system at time 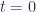is . Find an expression for the state at some later time , .

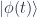\paragraph{A:}

Most of the work is already done. Computation of follows from 3.44

\paragraph{Q: (c)}

Suppose that an observable, specified by the operator , is measured for this system. What is the probabilbity that, at time 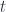, the result is obtained? Plot this probability as a function of time, showing the maximum and minimum values of the function, and the corresponding values of .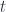

\paragraph{A:}

The language of questions like these attempt to bring some physics into the mathematics. The phrase “the result is obtained”, is really a statement that the operator , after measurement is found to have the eigenstate with numeric value 1.

We can calcuate the eigenvectors for this operator easily enough and find them to be 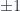. For the positive eigenvalue we can also compute the eigenstate to be

The question of what the probability for this measurement is then really a question asking for the computation of the amplitude

From 3.45 we find this probability to be

We have a simple superposition of two sinusuiods out of phase, periodic with period . I’d attempted a rough sketch of this on paper, but won’t bother scanning it here or describing it further.

\paragraph{Q: (d)}

Suppose an experimenter has control over the values of the parameters 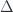and 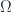. Explain how she might prepare the state .

\paragraph{A:}

For this part of the question I wasn’t sure what approach to take. I thought perhaps this linear combination of states could be made to equal one of the energy eigenstates, and if one could prepare the system in that state, then for certain values of and 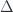one would then have this desired state.

To get there I note that we can express the states , and in terms of the eigenstates by inverting

Skipping all the algebra one finds

Unfortunately, this doesn’t seem helpful. I find

There’s no obvious way to pick 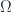and 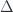to leave just or . When I did this on paper originally I got a different answer for this sum, but looking at it now, I can’t see how I managed to get that answer (it had no factors of in the result as the one above does).

3. One dimensional harmonic oscillator.

Consider a one-dimensional harmonic oscillator with the Hamiltonian

Denote the ground state of the system by , the first excited state by 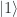and so on.

\paragraph{Q: (a)}
Evaluate and for arbitrary .

\paragraph{A:}

Writing in terms of the raising and lowering operators we have

so is proportional to

For we have

We are left with just

\paragraph{Q: (b)}

Suppose that at the system is prepared in the state

If a measurement of position were performaed immediately, sketch the propability distribution that a particle would be found within of . Justify how you construct the sketch.

\paragraph{A:}

The probability that we started in state and ended up in position is governed by the amplitude , and the probability of being within an interval , surrounding the point is given by

In the limit as , this is just the squared amplitude itself evaluated at the point , so we are interested in the quantity

We are given these wave functions in the supplemental formulas. Namely,

Substituting these into 3.57 we have

This \href{http://www.wolframalpha.com/input/?i=graph+e^(-x^2)+(1+

\paragraph{Q: (c)}

Now suppose the state given in (b) above were allowed to evolve for a time 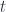, determine the expecation value of and at that time.

\paragraph{A:}

Our time evolved state is

The position expectation is therefore

We have already demonstrated that , so we must only expand the cross terms, but those are just . This leaves

For the squared position expectation

Noting that , and , so we see the last two terms are zero. The first two we can evaluate using our previous result 3.54 which was . This leaves

Since , we have

\paragraph{Q: (d)}

Now suppose that initially the system were prepared in the ground state , and then the resonance frequency is changed abrubtly from 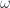to so that the Hamiltonian becomes

Immediately, an energy measurement is performed ; what is the probability of obtaining the result ?

\paragraph{A:}

This energy measurement , corresponds to an observation of state , after an initial observation of . The probability of such a measurement is

Note that

The wave functions above are

Putting the pieces together we have

Since this is an odd integral kernel over an even range, this evaluates to zero, and we conclude that the probability of measuring the specified energy is zero when the system is initially prepared in the ground state associated with the original Hamiltonian. Intuitively this makes some sense, if one thinks of the Fourier coefficient problem: one cannot construct an even function from linear combinations of purely odd functions.

Notes for Desai Chapter 26

[Click here for a PDF of this post with nicer formatting]

Motivation.

Chapter 26 notes for [1].

Guts

Trig relations.

To verify equations 26.3-5 in the text it’s worth noting that

and

So, for

the transformed coordinates are

and

This allows us to read off the rotation matrix. Without all the messy trig, we can also derive this matrix with geometric algebra.

Here we use the Pauli-matrix like identities

and also note that commutes with the bivector for the plane . We can also read off the rotation matrix from this.

Infinitesimal transformations.

Recall that in the problems of Chapter 5, one representation of spin one matrices were calculated [2]. Since the choice of the basis vectors was arbitrary in that exersize, we ended up with a different representation. For as found in (26.20) and (26.23) we can also verify easily that we have eigenvalues . We can also show that our spin kets in this non-diagonal representation have the following column matrix representations:

Verifying the commutator relations.

Given the (summation convention) matrix representation for the spin one operators

let’s demonstrate the commutator relation of (26.25).

Now we can employ the summation rule for sums products of antisymmetic tensors over one free index (4.179)

Continuing we get

General infinitesimal rotation.

Equation (26.26) has for an infinitesimal rotation counterclockwise around the unit axis of rotation vector

Let’s derive this using the geometric algebra rotation expression for the same

We note that and thus the exponential commutes with , and the projection component in the normal direction. Similarily anticommutes with . This leaves us with

For , this is

Position and angular momentum commutator.

Equation (26.71) is

Let’s derive this. Recall that we have for the position-momentum commutator

and for each of the angular momentum operator components we have

The commutator of interest is thus

A note on the angular momentum operator exponential sandwiches.

In (26.73-74) we have

Observe that

so from the first two terms of (10.99)

we get the desired result.

Trace relation to the determinant.

Going from (26.90) to (26.91) we appear to have a mystery identity

According to wikipedia, under derivative of a determinant, [3], this is good for small , and related to something called the Jacobi identity. Someday I should really get around to studying determinants in depth, and will take this one for granted for now.

References

[1] BR Desai. Quantum mechanics with basic field theory. Cambridge University Press, 2009.

[2] Peeter Joot. Notes and problems for Desai Chapter V. [online]. http://sites.google.com/site/peeterjoot/math2010/desaiCh5.pdf.

[3] Wikipedia. Determinant — wikipedia, the free encyclopedia [online]. 2010. [Online; accessed 10-December-2010]. http://en.wikipedia.org/w/index.php?title=Determinant&oldid=400983667.