[Click here for a PDF of this post with nicer formatting (especially if my latex to wordpress script has left FORMULA DOES NOT PARSE errors.)]
Disclaimer
This is an ungraded set of answers to the problems posed.
Question: Polymer stretching – “entropic forces” (2013 problem set 5, p1)
Consider a toy model of a polymer in one dimension which is made of 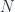 steps (amino acids) of unit length, going left or right like a random walk. Let one end of this polymer be at the origin and the other end be at a point
steps (amino acids) of unit length, going left or right like a random walk. Let one end of this polymer be at the origin and the other end be at a point  (viz. the rms size of the polymer) , so
(viz. the rms size of the polymer) , so 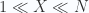 . We have previously calculated the number of configurations corresponding to this condition (approximate the binomial distribution by a Gaussian).
. We have previously calculated the number of configurations corresponding to this condition (approximate the binomial distribution by a Gaussian).
Part a
Using this, find the entropy of this polymer as  . The free energy of this polymer, even in the absence of any other interactions, thus has an entropic contribution,
. The free energy of this polymer, even in the absence of any other interactions, thus has an entropic contribution,  . If we stretch this polymer, we expect to have fewer available configurations, and thus a smaller entropy and a higher free energy.
. If we stretch this polymer, we expect to have fewer available configurations, and thus a smaller entropy and a higher free energy.
Part b
Find the change in free energy of this polymer if we stretch this polymer from its end being at  to a larger distance
to a larger distance  .
.
Part c
Show that the change in free energy is linear in the displacement for small  , and hence find the temperature dependent “entropic spring constant” of this polymer. (This entropic force is important to overcome for packing DNA into the nucleus, and in many biological processes.)
, and hence find the temperature dependent “entropic spring constant” of this polymer. (This entropic force is important to overcome for packing DNA into the nucleus, and in many biological processes.)
Typo correction (via email):
You need to show that the change in free energy is quadratic in the displacement  , not linear in
, not linear in  . The force is linear in
. The force is linear in  . (Exactly as for a “spring”.)
. (Exactly as for a “spring”.)
Answer
Entropy.
In lecture 2 probabilities for the sums of fair coin tosses were considered. Assigning  to the events
to the events 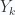 for heads and tails coin tosses respectively, a random variable
for heads and tails coin tosses respectively, a random variable  for the total of
for the total of 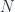 such events was found to have the form
such events was found to have the form

For an individual coin tosses we have averages 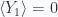 , and
, and 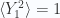 , so the central limit theorem provides us with a large
, so the central limit theorem provides us with a large  Gaussian approximation for this distribution
Gaussian approximation for this distribution

This fair coin toss problem can also be thought of as describing the coordinate of the end point of a one dimensional polymer with the beginning point of the polymer is fixed at the origin. Writing  for the total number of configurations that have an end point at coordinate
for the total number of configurations that have an end point at coordinate  we have
we have

From this, the total number of configurations that have, say, length  , in the large
, in the large 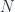 Gaussian approximation, is
Gaussian approximation, is

The entropy associated with a one dimensional polymer of length  is therefore
is therefore
Writing 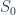 for this constant the free energy is
for this constant the free energy is

Change in free energy.
At constant temperature, stretching the polymer from its end being at  to a larger distance
to a larger distance  , results in a free energy change of
, results in a free energy change of

If  is assumed small, our constant temperature change in free energy
is assumed small, our constant temperature change in free energy  is
is

Temperature dependent spring constant.
I found the statement and subsequent correction of the problem statement somewhat confusing. To figure this all out, I thought it was reasonable to step back and relate free energy to the entropic force explicitly.
Consider temporarily a general thermodynamic system, for which we have by definition free energy and thermodynamic identity respectively


The differential of the free energy is

Forming the wedge product with  , we arrive at the two form
, we arrive at the two form

This provides the relation between free energy and the “pressure” for the system

For a system with a constant cross section  ,
,  , so the force associated with the system is
, so the force associated with the system is

or

Okay, now we have a relation between the force and the rate of change of the free energy

Our temperature dependent “entropic spring constant” in analogy with  , is therefore
, is therefore

Question: Independent one-dimensional harmonic oscillators (2013 problem set 5, p2)
Consider a set of 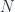 independent classical harmonic oscillators, each having a frequency
independent classical harmonic oscillators, each having a frequency 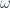 .
.
Part a
Find the canonical partition at a temperature  for this system of oscillators keeping track of correction factors of Planck constant. (Note that the oscillators are distinguishable, and we do not need
for this system of oscillators keeping track of correction factors of Planck constant. (Note that the oscillators are distinguishable, and we do not need  correction factor.)
correction factor.)
Part b
Using this, derive the mean energy and the specific heat at temperature  .
.
Part c
For quantum oscillators, the partition function of each oscillator is simply 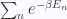 where
where  are the (discrete) energy levels given by
are the (discrete) energy levels given by 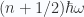 , with
, with 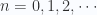 . Hence, find the canonical partition function for
. Hence, find the canonical partition function for 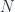 independent distinguishable quantum oscillators, and find the mean energy and specific heat at temperature
independent distinguishable quantum oscillators, and find the mean energy and specific heat at temperature  .
.
Part d
Show that the quantum results go over into the classical results at high temperature  , and comment on why this makes sense.
, and comment on why this makes sense.
Part e
Also find the low temperature behavior of the specific heat in both classical and quantum cases when  .
.
Answer
Classical partition function
For a single particle in one dimension our partition function is

with


we have
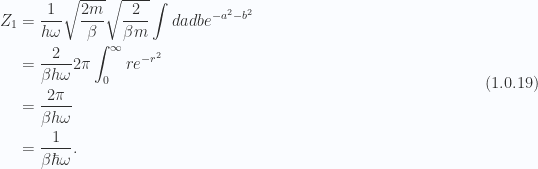
So for 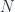 distinguishable classical one dimensional harmonic oscillators we have
distinguishable classical one dimensional harmonic oscillators we have

Classical mean energy and heat capacity
From the free energy

we can compute the mean energy

or

The specific heat follows immediately

Quantum partition function, mean energy and heat capacity
For a single one dimensional quantum oscillator, our partition function is
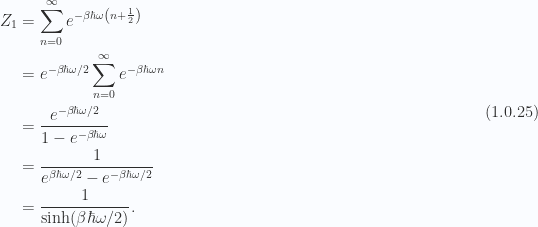
Assuming distinguishable quantum oscillators, our 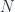 particle partition function is
particle partition function is

This time we don’t add the  correction factor, nor the
correction factor, nor the  indistinguishability correction factor.
indistinguishability correction factor.
Our free energy is

our mean energy is

or

This is plotted in fig. 1.1.

Fig 1.1: Mean energy for N one dimensional quantum harmonic oscillators
With  , our specific heat is
, our specific heat is

or

Classical limits
In the high temperature limit  , we have
, we have


so

or

matching the classical result of eq. 1.0.23. Similarly from the quantum specific heat result of eq. 1.0.31, we have

This matches our classical result from eq. 1.0.24. We expect this equivalence at high temperatures since our quantum harmonic partition function eq. 1.0.26 is approximately

This differs from the classical partition function only by this factor of  . While this alters the free energy by
. While this alters the free energy by  , it doesn’t change the mean energy since
, it doesn’t change the mean energy since  . At high temperatures the mean energy are large enough that the quantum nature of the system has no significant effect.
. At high temperatures the mean energy are large enough that the quantum nature of the system has no significant effect.
Low temperature limits
For the classical case the heat capacity was constant ( ), all the way down to zero. For the quantum case the heat capacity drops to zero for low temperatures. We can see that via L’hopitals rule. With
), all the way down to zero. For the quantum case the heat capacity drops to zero for low temperatures. We can see that via L’hopitals rule. With 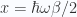 the low temperature limit is
the low temperature limit is
We also see this in the plot of fig. 1.2.

Fig 1.2: Specific heat for N quantum oscillators
Question: Quantum electric dipole (2013 problem set 5, p3)
A quantum electric dipole at a fixed space point has its energy determined by two parts – a part which comes from its angular motion and a part coming from its interaction with an applied electric field  . This leads to a quantum Hamiltonian
. This leads to a quantum Hamiltonian

where  is the moment of inertia, and we have assumed an electric field
is the moment of inertia, and we have assumed an electric field  . This Hamiltonian has eigenstates described by spherical harmonics
. This Hamiltonian has eigenstates described by spherical harmonics  , with
, with 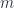 taking on
taking on  possible integral values,
possible integral values,  . The corresponding eigenvalues are
. The corresponding eigenvalues are

(Recall that  is the total angular momentum eigenvalue, while
is the total angular momentum eigenvalue, while 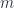 is the eigenvalue corresponding to
is the eigenvalue corresponding to  .)
.)
Part a
Schematically sketch these eigenvalues as a function of  for
for  .
.
Part b
Find the quantum partition function, assuming only 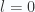 and
and  contribute to the sum.
contribute to the sum.
Part c
Using this partition function, find the average dipole moment 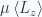 as a function of the electric field and temperature for small electric fields, commenting on its behavior at very high temperature and very low temperature.
as a function of the electric field and temperature for small electric fields, commenting on its behavior at very high temperature and very low temperature.
Part d
Estimate the temperature above which discarding higher angular momentum states, with  , is not a good approximation.
, is not a good approximation.
Answer
Sketch the energy eigenvalues
Let’s summarize the values of the energy eigenvalues 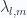 for
for 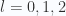 before attempting to plot them.
before attempting to plot them.
For 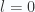 , the azimuthal quantum number can only take the value
, the azimuthal quantum number can only take the value  , so we have
, so we have


For  we have
we have

so we have



For  we have
we have

so we have



These are sketched as a function of  in fig. 1.3.
in fig. 1.3.

Fig 1.3: Energy eigenvalues for l = 0,1, 2
Partition function
Our partition function, in general, is
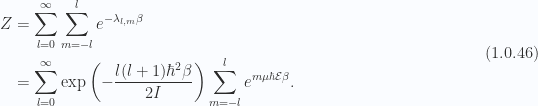
Dropping all but  terms this is
terms this is

or

Average dipole moment
For the average dipole moment, averaging over both the states and the partitions, we have
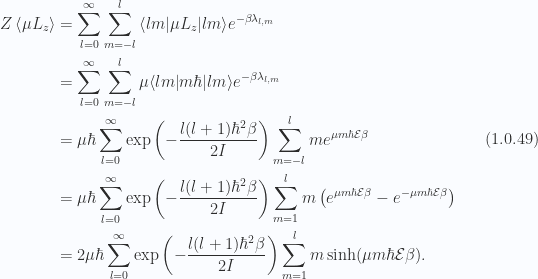
For the cap of  we have
we have

or

This is plotted in fig. 1.4.

Fig 1.4: Dipole moment
For high temperatures  or
or  , expanding the hyperbolic sine and cosines to first and second order respectively and the exponential to first order we have
, expanding the hyperbolic sine and cosines to first and second order respectively and the exponential to first order we have

Our dipole moment tends to zero approximately inversely proportional to temperature. These last two respective approximations are plotted along with the all temperature range result in fig. 1.5.

Fig 1.5: High temperature approximations to dipole moments
For low temperatures 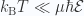 , where
, where  we have
we have

Provided the electric field is small enough (which means here that  ) this will look something like fig. 1.6.
) this will look something like fig. 1.6.

Fig 1.6: Low temperature dipole moment behavior
Approximation validation
In order to validate the approximation, let’s first put the partition function and the numerator of the dipole moment into a tidier closed form, evaluating the sums over the radial indices  . First let’s sum the exponentials for the partition function, making an
. First let’s sum the exponentials for the partition function, making an 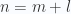

With a substitution of  , we have
, we have

Now we can sum the azimuthal exponentials for the dipole moment. This sum is of the form

With  , and
, and  , we have
, we have

we have
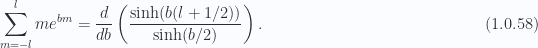
With a little help from Mathematica to simplify that result we have

We can now express the average dipole moment with only sums over radial indices 

So our average dipole moment is

The hyperbolic sine in the denominator from the partition function and the difference of hyperbolic sines in the numerator both grow fast. This is illustrated in fig. 1.7.

Fig 1.7: Hyperbolic sine plots for dipole moment
Let’s look at the order of these hyperbolic sines for large arguments. For the numerator we have a difference of the form

For the hyperbolic sine from the partition function we have for large 
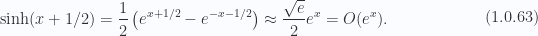
While these hyperbolic sines increase without bound as  increases, we have a negative quadratic dependence on
increases, we have a negative quadratic dependence on  in the
in the  contribution to these sums, provided that is small enough we can neglect the linear growth of the hyperbolic sines. We wish for that factor to be large enough that it dominates for all
contribution to these sums, provided that is small enough we can neglect the linear growth of the hyperbolic sines. We wish for that factor to be large enough that it dominates for all  . That is
. That is

or

Observe that the RHS of this inequality, for  satisfies
satisfies

So, for small electric fields, our approximation should be valid provided our temperature is constrained by







